Какое наименьшее значение может принимать периметр неравнобедренного
треугольника с целыми длинами сторон.
Пусть ( a,b,c ) — стороны треугольника
Длина стороны может принимать значения от 1 до бесконечности, но очевидно, что нас будут устраивать только маленькие числа.
Так как треугольник неравнобедренный, то должно выполнятся равенство ( a>b>c ) , пусть ( a=1,b=2,c=3 ) — вроде как устраивается ответ, но вспомним неравенство треугольника
Значит будем искать дальше, увеличим все на 1, возьмем ( a=2,b=3,c=4 )
Видео:Как вычислить периметр #геометрия #задача #треугольник #периметрСкачать

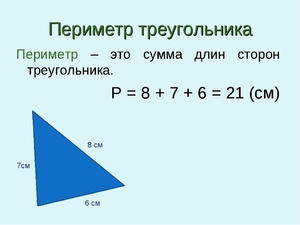
Формулы определения периметра, площади и сторон треугольника
Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.
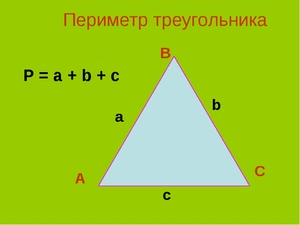
Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.
Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:
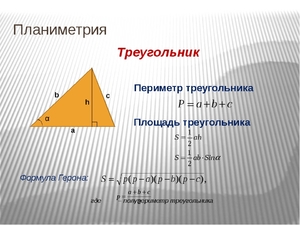
Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.
Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:
Из этого видео вы узнаете, как найти площадь треугольника.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Классификация треугольников
Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.
- Равноугольный: все вершины равны 60°, будет и равносторонним.
- Равнобедренный: при равенстве двух граней углы на основании равны.
- Разноугольный: все вершины разные, ребра у него тоже разные.
- Прямоугольный: один угол равен 90°, примыкающие грани называются катеты, противолежащая — гипотенуза. Бывает равнобедренным (катеты равны) или разноугольным (катеты разные).
- Тупоугольный: один угол больше 90°. Может быть равнобедренным или разноугольным.
Видео:Урок. Как найти периметр треугольника. Математика 2 класс. #учусьсамСкачать

Описание
Чтобы описать любой треугольник, достаточно указать:
- Одну сторону и прилегающие к ней углы.
- Две стороны и угол между ними.
- Три стороны.
Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:
Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.
Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.
Видео:Математика 2 класс. «Периметр треугольника, прямоугольника и квадрата»Скачать

Примеры
Известно, что одна грань равна 9 см и прилегающие углы по 60 градусов. Тогда из того, что сумма углов всегда равна 180°, получаем: 180=60+60+x; x=180—120=60. Все три вершины по 60°, значит, все стороны равны. Периметр составляет P=9+9+9=27 см, полупериметр p=13,5 см. Чтобы найти высоту, нужно опустить перпендикуляр из вершины на основание, получим прямоугольный треугольник с гипотенузой 9 см, катетом 4,5 см и катетом неизвестной длины, равным искомой высоте: 9*9—4,5*4,5=60,75=h 2 .
Высота равна корню квадратному из 60,75 или 7,79422863406 см. Умножаем основание на высоту, делим пополам и получаем площадь: 7,79422863406*9/2=35,074028853 см 2 . Если находить площадь по формуле Герона через полупериметр и ребра, ответ будет одинаковый:
S=√(13,5·(13,5—9)·(13,5—9)·(13,5—9))=35,074028853 см 2 .
Следующий пример с разносторонним треугольником. Дано: AB=12 см, BC=10 см, CA=8 см. Требуется найти периметр и площадь фигуры. P=a+b+c=BC+CA+AB=10 см+8 см+12 см=30 см. Площадь находим по формуле Герона, подставляя в нее уже известные значения, учитывая, что p=0,5Р; p=15 см. S=√(p·(p—a)·(p—b)·(p—c))=√(15·(15—10)·(15—8)·(15—12))=√15·5·7·3=√1575=39,686269666 см 2 .
Рассмотрим пример, когда известны два катета прямоугольного треугольника. Допустим, они имеют значения два и четыре метра. Тогда гипотенуза будет равна корню квадратному из суммы квадратов катетов √2 2 +4 2 =4,472135955 м. Периметр 2+4+4,472135955=10,472135955. Площадь равна половине произведения катетов S=2·4=8м 2 .
Когда известны две стороны и угол между ними, остается найти только третью сторону по теореме косинусов. Пусть известные стороны составляют значения 16 и 28 метров, а угол между ними будет в 60 градусов, тогда третья сторона будет равна корню квадратному из этого выражения 16 2 +28 2 — 2·16·28·0,5, что составит значение в 24,3310501212 м. Периметр равен 16+28+24,3310501212=68,3310501212≈68,33 м. Полупериметр будет 34,165 м. Подставляя полученные значения в формулу Герона, найдем площадь S=√(34,165·(34,165—16)·(34,165—28)·(34,165—24,33))=193,982314238 м 2 .
Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.
Видео:КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Видео
Это видео поможет вам закрепить полученные знания.
Видео:Тест. Как найти периметр треугольника. Математика 2 класс. #учусьсамСкачать

Как найти периметр треугольника
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Как найти периметр?Скачать

Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Видео:Найдите периметр треугольникаСкачать

Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
🔍 Видео
Как найти периметрСкачать

№156. Периметр треугольника ABC равен 15 см. Сторона ВС больше стороны АВ на 2 см, а сторона ABСкачать

Периметр прямоугольника. Как найти периметр прямоугольника?Скачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Хитрый периметрСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Задачи на периметр труегольника. Геометрия 7 класс. Две задачи.Скачать

Как найти сторону треугольника по его периметруСкачать

Что такое периметр. Как найти периметр многоугольника?Скачать

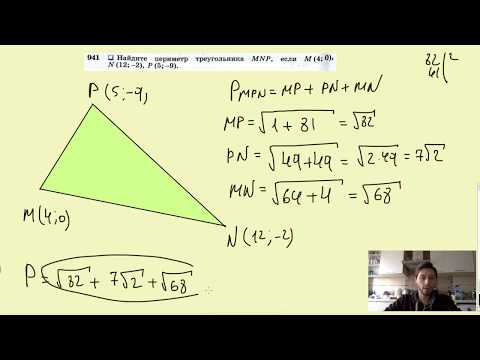
№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать
№91. Периметр треугольника равен 48 см, а одна из сторон равна 18 см. Найдите две другиеСкачать