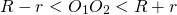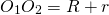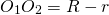Выясним, каким может быть взаимное расположение двух окружностей.
Две окружности могут пересекаться, не пересекаться либо касаться друг друга.
I. Пересекающиеся окружности имеют две общие точки.
Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:
II. Не пересекающиеся окружности не имеет общих точек.
Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:

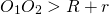
III. Касающиеся окружности имеют одну общую точку — точку касания.
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
При внутреннем касании расстояние между центрами равно разности радиусов:
Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0.
Видео:Геометрия Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второйСкачать

Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Видео:Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай — окружности совпадают (это одна и та же окружность) | ||
| Окружности не касаются друг друга | r1 + r2″ /> | |
| Одна окружность содержится внутри другой и не касается ее | ||
| Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше | |
| Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
Сначала калькулятор находит отрезок a
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Видео:Теорема о числе точек пересечения двух окружностейСкачать

ПЕРЕСЕЧЕНИЕ ДВУХ ОКРУЖНОСТЕЙ
Видео:№662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°, ∪BC= 70°.Скачать

ПЕРЕСЕЧЕНИЕ ДВУХ ОКРУЖНОСТЕЙ
ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР
Скачать всю книгу Ж. АДАМАР «ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ» в хорошем качестве
Ниже посмотрите текст для быстрого ознакомления(формулы отображаются не корректно):
68. Две окружности не могут иметь более двух общих точек
по теореме п. 57.
Теорема. Если две окружности пересекаются, то прямая,
соединяющая их центры, перпендикулярна к общей хорде и делит
её на две равные части. Если они имеют только одну общую
точку, то эта точка лежит на линии центров, и обратно.
В самом деле, линия центров обеих окружностей является их
общей осью симметрии. Если две окружности пересекаются в некоторой
точке, не лежащей на линии центров, то второй их общей точкой
будет точка, симметричная с первой относительно линии центров.
Если общая точка — единственная, то она необходимо должна
лежать на линии центров.
Обратно, если имеется общая точка, лежащая на линии центров,
то эта точка будет единственной общей точкой. Действительно, вторая
общая точка окружностей лежала бы либо на линии центров,
либо вне её: в первом случае обе окружности имели бы общий
диаметр, во втором случае существовала бы и третья точка пересечения.
В обоих случаях окружности совпадали бы между собой.
69. Говорят, что две кривые касаются друг друга, если они
имеют общую касательную в их общей точке.
‘На основании предыдущей теоремы это определение в случае
двух окружностей сводится к следующему:
Две окружности касаются друг друга, если они имеют только
одну общую точку, потому что общая точка, через которую проходит
общая касательная к окружностям, необходимо является точкой
линии центров, и обратно
(п. 58, следствие).
70. Пусть О, Ог — центры
двух окружностей, радиусы
которых R, Rr; предположим
для определённости, что
/?r=g/?.
При этом могут иметь место
следующие пять случаев:
l°.OOf >/? + /?’ (черт. 71).
Предположим, что М —
точка, лежащая на окружности
О1 или внутри её, так что OrM R -f- Rr — OrM R.
Таким образом, всякая точка, взятая внутри или на второй окружности,
является внешней по отношению к первой, а всякая точка внутри
или на первой окружности — внешней по отношению ко второй.
Две окружности, как говорят, расположены одна вне другой.
2°. OOr = R—Rr. В таком случае 00′ можно рассматривать как
сумму двух отрезков ОЛ и О’А (черт. 72), соответственно равных R
и R!. Точка А — общая; кроме того, ко всякой другой точке можно
применить предыдущие рассуждения. Следовательно, окружности
касаются друг друга внешним образом.
3°. R -j- R! OOf R — Rr. В этом случае R заключается между
суммой и разностью двух отрезков ООг и Rr.
Таким образом, из двух точек А и В, в которых окружность О
пересекает линию центров, одна внешняя, а другая—внутренняя относительно
окружности—О'(черт. 73); отсюда следует, что окружность О,
представляющая собой линию, идущую из точки А в точку В, встретит
вторую окружность в точке, отличной от А и В, т. е. в точке,
не лежащей на линии центров. Следовательно, обе окружности имеют
две общие точки. Окружности называются пересекающимися.
4°. OOr = R — Rr. В этом случае 001 можно рассматривать как
разность двух отрезков О А и О1 А (черт. 74), соответственно равных
R и R Точка А их линии центров — общая, так что окружности
касаются.
Пусть М — точка, лежащая на окружности Ог или внутри этой
окружности. Мы будем иметь
ОМ g OOr + О’М g OOr + Rr,
т. е. ОМ ПЕРЕСЕЧЕНИЕ ДВУХ ОКРУЖНОСТЕЙ
📸 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

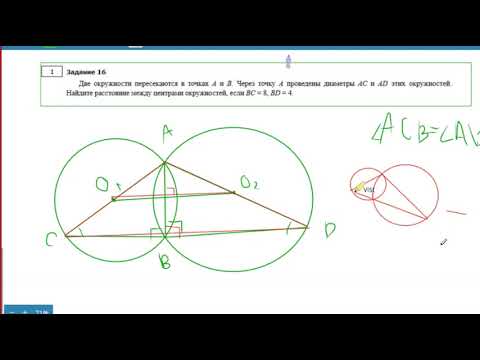
Геометрия Две окружности пересекаются в точках A и B. Через точку A проведены диаметры AC и AD этихСкачать

№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

Две окружности пересекаются в точках A и B Через точку A проведены диаметры AC и AD этих окружностеСкачать
Геометрия В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимноСкачать

8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Две окружности пересекаются, если радиус одной ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Взаимное расположение окружностей. Точки пересечения окружностейСкачать

Геометрия Хорды AB и CD окружности пересекаются в точке M (см. рис.). Докажите, что угол AMC = 1/2Скачать

Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Касательные к окружности пересекаются в точке. Теорема и решение задач. Геометрия 7-8 классСкачать

Алгоритмы. Пересечение окружностейСкачать

Геометрия Докажите, что если хорды AB и CD окружности пересекаются в точке M, то AM٠MB = DM٠MCСкачать

ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

9 класс, 8 урок, Взаимное расположение двух окружностейСкачать