- Решение уравнений cos(x)
- cosx = 1
- cosx = -1
- cosx = 0
- cosx = 1/2
- Другие уравнения с косинусом
- Узнать ещё
- cosx=0
- Косинус
- Коcинус – одна из тригонометрических функций. Значение косинуса определяется для угла или для числа (в этом случае используют числовую окружность).
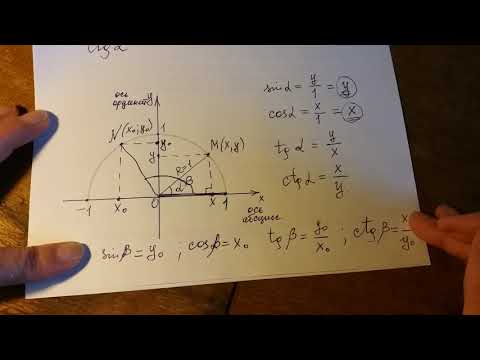
- Аргумент и значение
- Косинус острого угла
- Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.
- Косинус острого угла больше (0) и меньше (1)
- Косинус числа
- Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.
- Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.
- Косинус любого угла
- Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
- Знаки косинуса по четвертям
- Связь с другими тригонометрическими функциями:
- Функция (y=cos)
- 📹 Видео
Видео:ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Решение уравнений cos(x)
— это абсцисса точки на единичной окружности, соответствующей углу .
cosx = 1
cosx = 1
На единичной окружности имеется лишь одна точка с абсциссой 1.
Эта точка соответствует бесконечному множеству углов: 0, , , , . Все они получаются из нулевого угла прибавлением целого числа полных углов . Все эти углы могут быть записаны одной формулой:
где, — множество целых чисел.
cosx = -1
cosx = -1
Снова, на единичной окружности есть всего лишь одна точка с абсциссой -1.
Эта точка соответствует углу и всем углам, отличающихся от на несколько полных оборотов в обе стороны.
cosx = 0
cosx = 0
Точки с абсциссой образуют на единичной окружности вертикальную диаметральную пару.
Все углы, отвечающие этим точкам, получаются из прибавлением целого числа (полуоборотов):
cosx = 1/2
Имеем вертикальную пару точек с абсциссой 1/2.
Все углы, соответствующие верхней точке, описываются формулой:
Все углы, соответствующие нижней точке, описываются формулой:
Обе формулы можно записать одной формулой:
Другие уравнения с косинусом
Остальные уравнения с косинусом решаются аналогично:
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Узнать ещё
Знание — сила. Познавательная информация
Видео:Тригонометрическая окружность. Как выучить?Скачать

cosx=0
Эта ассоциация помогает легко запомнить формулу для решения тригонометрического уравнения cosx=0.
Используем ассоциацию косинус-колобок.
Начинаются они одинаково, на ко-. Колобок движется влево-вправо, в силу особенностей своей фигуры. А влево-вправо на координатной плоскости происходит движение вдоль оси ox. Значит косинус — это x.
Для решения уравнения cosx=0 нам нужно найти точки, в которых косинус обращается в нуль. Как и в других частных случаях косинуса, решение ищем на единичной окружности, то есть на окружности с радиусом R=1.
Итак, cosx=0, косинус — это x, значит, двигаться ни влево, ни вправо не надо (колобок подпрыгнул на месте:)).
На единичной окружности x=0 соответствуют две точки: одна вверху, это п/2, другая — внизу, -п/2. Чтобы из одной точки попасть в другую, надо пройти половину окружности, то есть п.
Но через каждый интервал длиной п мы будет получать все новые и новые точки, в которых косинус равен нулю.
Чтобы учесть все такие точки, к первой точке прибавляем пn, где n — целое число (то есть принадлежит Z).
Таким образом, решение уравнения cosx=0 есть множество точек x=п/2+пn, где n — целое число. И соответствующий чертеж для иллюстрации ассоциации:
Видео:Таблица значений тригонометрических функций - как её запомнить!!!Скачать

Косинус
Коcинус – одна из тригонометрических функций. Значение косинуса определяется для угла или для числа (в этом случае используют числовую окружность).
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Аргумент и значение
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше (0) и меньше (1)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Косинус числа
Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи : (frac) , (frac) , (-2π).
Например, для числа (frac) — косинус будет равен (frac<sqrt>) . А для числа (-) (frac) он будет равен (-) (frac<sqrt>) (приблизительно (-0,71)).
Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице .
Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Видео:Отбор корней по окружностиСкачать

Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать — проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.
И, наконец, угол больше (360°) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).
Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
— там, где значения на оси от (0) до (1), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от (0) до (-1), косинус будет иметь знак минус (II и III четверти – фиолетовая область).
Пример. Определите знак (cos 1).
Решение: Найдем (1) на тригонометрическом круге. Будем отталкиваться от того, что (π=3,14). Значит единица, примерно, в три раза ближе к нулю (точке «старта»).
Если провести перпендикуляр к оси косинусов, то станет очевидно, что (cos1) – положителен.
Ответ: плюс.
Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Связь с другими тригонометрическими функциями:
— синусом того же угла (или числа): основным тригонометрическим тождеством (sin^2x+cos^2x=1)
— тангенсом того же угла (или числа): формулой (1+tg^2x=) (frac)
— котангенсом и синусом того же угла (или числа): формулой (ctgx=) (frac<cos>)
Другие наиболее часто применяемые формулы смотри здесь .
Видео:Синус, косинус, тангенс и котангенс углов от 0 до 180 градусов.Скачать
Функция (y=cos)
Если отложить по оси (x) углы в радианах, а по оси (y) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной функции называется косинусоида и обладает следующими свойствами:
— область определения – любое значение икса: (D(cos )=R)
— область значений – от (-1) до (1) включительно: (E(cos )=[-1;1])
— четная: (cos(-x)=cos)
— периодическая с периодом (2π): (cos(x+2π)=cos)
— точки пересечения с осями координат:
ось абсцисс: (() (frac) (+πn),(;0)), где (n ϵ Z)
ось ординат: ((0;1))
— промежутки знакопостоянства:
функция положительна на интервалах: ((-) (frac) (+2πn;) (frac) (+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: (() (frac) (+2πn;) (frac) (+2πn)), где (n ϵ Z)
— промежутки возрастания и убывания:
функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
— максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).
📹 Видео
🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Тригонометрия. Значения синуса и косинуса углов 0°,90°,180°, 270 °, 360° . 10-11 классСкачать

9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

Как найти значения синуса и косинуса, НЕ запоминая!Скачать

Тригонометрическая окружность для непонимающихСкачать

Формулы приведения - как их легко выучить!Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

























