Код паскаля для треугольника (3 видео) | Курс школьной геометрии

Определить возможность существования треугольника по сторонам

Содержание

Задача
Решение
Треугольник Паскаля
Программа Python для печати треугольника Паскаля
Вступление
Алгоритм печати треугольника Паскаля в Python
Способ 2
Способ 3
🌟 Видео

Задача

Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.

Дано: a , b , c – стороны предполагаемого треугольника.

Требуется сравнить длину каждого отрезка-стороны с суммой двух других. Если хотя бы в одном случае отрезок окажется больше суммы двух других, то треугольника с такими сторонами не существует.

Решение

Ниже приведены решения задачи на языке программирования Паскаль двумя способами. В первом случае все стороны проверяются в одном операторе if; во втором случае каждое условие проверяется отдельно, а программа содержит вложенные операторы if-else.

Программа 1 (предпочтительный способ решения):

В языке Паскаль логический оператор and имеет приоритет над операторам >, if проверяется, что каждая из сторон меньше суммы других. Если хотя бы одна будет больше, то все логическое выражение вернет ложь ( false ). В таком случае сработает ветка else .

В данном случае существование треугольника проверяется по-этапно. Если первое условие возвращает ложь, то программа переходит к последнему else. Если же первое условие соблюдено, то поток выполнения программы оказывается у вложенного if. Здесь проверяется уже второе условие. Если оно возвращает ложь, то программа переходит к предпоследнему else. Если и второе логическое выражение возвращает истину (true), то программа идет к третьему условию. При его соблюдении выполняется тело самого вложенного оператора if. При его несоблюдении сработает самое вложенное else.

Несмотря на то, что данная программа кажется длиннее, в определенных ситуациях она может выполняться быстрее, чем первая. Здесь если внешнее if возвращает ложь, то остальные логические выражения вообще не проверяются. В первой программе могут и проверяться (это зависит от особенностей языка программирования).

Видео:Треугольник ПаскаляСкачать

Треугольник Паскаля

Треугольник Паскаля представляет собой треугольный массив биномиальных коэффициентов. Напишите функцию, которая принимает целочисленное значение n в качестве входных данных и печатает первые n строк треугольника Паскаля. Ниже приведены первые 6 рядов треугольника Паскаля.

Способ 1 (O (n ^ 3) сложность времени)
Количество записей в каждой строке равно номеру строки. Например, в первой строке указано «1», во второй строке — «1 1», в третьей строке — «1 2 1», … и т. Д. Каждая запись в строке является значением биномиального коэффициента . Значение i- й записи в строке номера строки равно C (line, i) . Значение можно рассчитать по следующей формуле.

Простой метод — запустить два цикла и вычислить значение биномиального коэффициента во внутреннем цикле.

// C ++ код для треугольника Паскаля
#include

int binomialCoeff( int n, int k);

// Функция для печати первой
// n строк Паскаля
// Треугольник

void printPascal( int n)

// перебираем каждую строку и

// печатаем записи в нем

for ( int line = 0; line

// Каждая строка имеет номер

// целые числа равны строке

for ( int i = 0; i

int binomialCoeff( int n, int k)

for ( int i = 0; i

// Java-код для треугольника Паскаля

// Функция для печати первой

// n линий треугольника Паскаля

static void printPascal( int n)

// перебираем каждую строку

// и печатаем записи в нем

for ( int line = 0 ; line

// Каждая строка имеет номер

// целые числа равны номеру строки

for ( int i = 0 ; i

// Ссылка на детали этой функции

static int binomialCoeff( int n, int k)

for ( int i = 0 ; i

public static void main(String args[])

/ * Этот код предоставлен Никитой Тивари. * /

# Python 3 код для треугольника Паскаля
# Простая O (n ^ 3)
# программа для
# Треугольник Паскаля

# Функция для печати
# первые n строк
# Треугольник Паскаля

# Перебирать каждую строку

# и распечатать записи в нем

for line in range ( 0 , n) :

# Каждая строка имеет номер

# целые числа равны строке

for i in range ( 0 , line + 1 ) :

print (binomialCoeff(line, i),

def binomialCoeff(n, k) :

for i in range ( 0 , k) :

res = res / / (i + 1 )

# Этот код предоставлен Никитой Тивари.

// код C # для треугольника Паскаля

// Функция для печати первой

// n линий треугольника Паскаля

static void printPascal( int n)

// перебираем каждую строку

// и печатаем записи в нем

for ( int line = 0; line

// Каждая строка имеет номер

// целые числа равны номеру строки

for ( int i = 0; i

// Ссылка на детали этой функции

static int binomialCoeff( int n, int k)

for ( int i = 0; i

public static void Main()

/ * Этот код предоставлен vt_m. * /

// Реализация PHP для
// Треугольник Паскаля

// для деталей этой функции

function binomialCoeff( $n , $k )

for ( $i = 0; $i $k ; ++ $i )

// Функция для печати первой
// n строк Паскаля
// Треугольник

function printPascal( $n )

// перебираем каждую строку и

// печатаем записи в нем

for ( $line = 0; $line $n ; $line ++)

// Каждая строка имеет номер

// целые числа равны строке

for ( $i = 0; $i $line ; $i ++)

echo «» .binomialCoeff( $line , $i ). » » ;

// Этот код предоставлен Митхун Кумар
?>

Выход :

Временная сложность этого метода O (n ^ 3). Ниже приведены оптимизированные методы.

Метод 2 (O (n ^ 2) время и O (n ^ 2) дополнительное пространство)
Если мы подойдем ближе к треугольнику, мы увидим, что каждая запись является суммой двух значений над ней. Таким образом, мы можем создать 2D-массив, в котором хранятся ранее сгенерированные значения. Чтобы сгенерировать значение в строке, мы можем использовать ранее сохраненные значения из массива.

// C ++ программа для треугольника Паскаля
// AO (n ^ 2) время и O (n ^ 2) дополнительное пространство
// метод для треугольника Паскаля
#include

using namespace std;

void printPascal( int n)

// Вспомогательный массив для хранения

// генерируемые значения треугольника пскала

// перебираем каждую строку и

// напечатать в нем целое число

for ( int line = 0; line

// Каждая строка имеет количество целых чисел

// равно номеру строки

for ( int i = 0; i

// Первое и последнее значения в каждой строке равны 1

if (line == i || i == 0)

// Другие значения являются просто суммой значений

// вверху и слева вверху

arr[line][i] = arr[line — 1][i — 1] +

// Этот код предоставлен Code_Mech.

// C программа для треугольника Паскаля
// AO (n ^ 2) время и O (n ^ 2) дополнительное пространство
// метод для треугольника Паскаля

void printPascal( int n)

<
// Вспомогательный массив для хранения
// генерируемые значения треугольника пскала

// Перебираем каждую строку и печатаем в ней целые числа

for ( int line = 0; line

// Каждая строка имеет количество целых чисел

// равно номеру строки

for ( int i = 0; i

// Первое и последнее значения в каждой строке равны 1

if (line == i || i == 0)

// Другие значения являются просто суммой значений

// вверху и слева вверху

arr[line][i] = arr[line-1][i-1] + arr[line-1][i];

printf ( «%d » , arr[line][i]);

// Java-программа для треугольника Паскаля
// AO (n ^ 2) время и O (n ^ 2) дополнительно
// космический метод для треугольника Паскаля

public static void main (String[] args) <

public static void printPascal( int n)

<
// Вспомогательный массив для хранения сгенерированных значений треугольника Паскаля

int [][] arr = new int [n][n];

// Перебираем каждую строку и печатаем в ней целые числа

for ( int line = 0 ; line

// Каждая строка имеет число целых чисел, равное номеру строки

for ( int i = 0 ; i

// Первое и последнее значения в каждой строке равны 1

if (line == i || i == 0 )

else // Другие значения являются суммой значений чуть выше и выше слева

arr[line][i] = arr[line- 1 ][i- 1 ] + arr[line- 1 ][i];

# Python3 программа для треугольника Паскаля

# AO (n ^ 2) время и O (n ^ 2) дополнительно
# космический метод для треугольника Паскаля

def printPascal(n: int ):

# Вспомогательный массив для хранения

# генерируемые значения треугольника Паскаля

arr = [[ 0 for x in range (n)]

for y in range (n)]

# Перебирать каждую строку

# и выведите в нем целое число

for line in range ( 0 , n):

# Каждая строка имеет номер

# целые числа, равные номеру строки

for i in range ( 0 , line + 1 ):

# Первое и последнее значения

# в каждом ряду 1

if (i is 0 or i is line):

print (arr[line][i], end = » » )

# Другие значения являются суммой значений

# чуть выше и выше слева

arr[line][i] = (arr[line — 1 ][i — 1 ] +

print (arr[line][i], end = » » )

# Этот код добавлен
# Санджу Мадерна

// C # программа для треугольника Паскаля
// AO (n ^ 2) время и O (n ^ 2) дополнительно
// космический метод для треугольника Паскаля

public static void printPascal( int n)

// Вспомогательный массив для хранения
// сгенерированные значения треугольника Паскаля

int [,] arr = new int [n, n];

// перебираем каждую строку
// и вывести в нем целое число

for ( int line = 0; line

// Каждая строка имеет номер

// целые числа равны номеру строки

for ( int i = 0; i

// Первые и последние значения

// в каждом ряду 1

if (line == i || i == 0)

else // Другие значения являются суммой значений

// чуть выше и выше слева

arr[line, i] = arr[line — 1, i — 1] +

public static void Main ()

// Этот код добавлен
// Аканкша Рай (Abby_akku)

// PHP программа для треугольника Паскаля
// AO (n ^ 2) время и O (n ^ 2) дополнительное пространство
// метод для треугольника Паскаля

function printPascal( $n )

// Вспомогательный массив для хранения

// генерируемые значения треугольника пскала

$arr = array ( array ());

// перебираем каждую строку и

// напечатать в нем целое число

for ( $line = 0; $line $n ; $line ++)

// Каждая строка имеет количество целых чисел

// равно номеру строки

for ( $i = 0; $i $line ; $i ++)

// Первое и последнее значения в каждой строке равны 1

if ( $line == $i || $i == 0)

$arr [ $line ][ $i ] = 1;

// Другие значения являются просто суммой значений

// вверху и слева вверху

$arr [ $line ][ $i ] = $arr [ $line — 1][ $i — 1] +

echo $arr [ $line ][ $i ] . » » ;

// Этот код добавлен
// Аканкша Рай
?>

Этот метод может быть оптимизирован для использования O (n) дополнительного пространства, так как нам нужны значения только из предыдущей строки. Таким образом, мы можем создать вспомогательный массив размера n и перезаписать значения. Ниже приведен другой метод, использующий только O (1) дополнительное пространство.

Метод 3 (O (n ^ 2) время и O (1) дополнительное пространство)
Этот метод основан на методе 1. Мы знаем, что i- я запись в строке номера строки является биномиальным коэффициентом C (line, i), и все строки начинаются со значения 1. Идея состоит в том, чтобы вычислить C (line, i), используя C ( линия, я-1) . Его можно рассчитать за время O (1), используя следующее.

// C ++ программа для треугольника Паскаля
// AO (n ^ 2) время и O (1) дополнительное пространство
// функция для треугольника Паскаля
#include

using namespace std;

void printPascal( int n)

for ( int line = 1; line

int C = 1; // используется для представления C (line, i)

Видео:#26. Треугольник Паскаля как пример работы вложенных циклов | Python для начинающихСкачать

Программа Python для печати треугольника Паскаля

В этом руководстве мы обсудим, как напечатать треугольник Паскаля с помощью программы Python. Но сначала давайте разберемся, что такое треугольник Паскаля.

Видео:Несколько красивых свойств треугольника ПаскаляСкачать

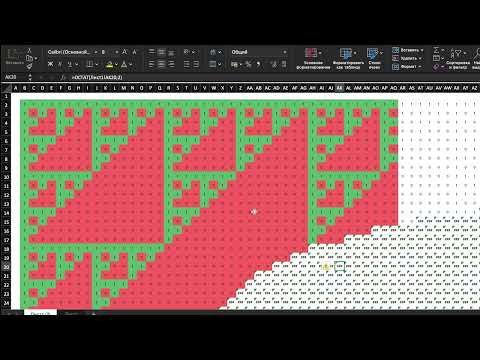
Вступление

Треугольник Паскаля – это захватывающая математическая концепция, в которой треугольный массив формируется путем суммирования смежных элементов в предыдущей строке. Проще говоря, каждое число генерируется путем суммирования соседней строки, а внешние края треугольника всегда равны 1. Он назван в честь известного французского математика Блеза Паскаля. Ниже представлен треугольник Паскаля.

На изображении выше первая строка равна 1. Вторая строка содержит 2 единицы, а третья строка – 1 2 1, которая формируется путем суммирования указанной выше строки. Таким образом, он следует альтернативному шаблону во всем треугольнике и так далее.

Видео:Числа сочетаний. Треугольник Паскаля | Ботай со мной #059 | Борис Трушин |Скачать

Алгоритм печати треугольника Паскаля в Python

Ниже приведен шаг, используемый для печати треугольника Паскаля.

Шаг – 1: Получение данных от пользователя для определения количества строк.
Шаг – 2: Объявление пустого списка, в котором будут храниться значения.
Шаг – 3: Используя цикл for, который будет перебирать от 0 до n – 1, добавить подсписки в список.
Шаг – 4: Теперь добавить 1 в список.
Шаг – 5: Используя цикл for, определить значение числа внутри соседней строки треугольника.
Шаг – 6: Распечатать треугольник Паскаля в соответствии с форматом.
Шаг – 7: Выход.

Давайте разберемся с реализацией алгоритма в программе Python:

Запускаем программу еще раз.

В приведенной выше программе мы взяли несколько строк от пользователя в качестве входных. Мы объявили пустой список. Затем мы использовали цикл for, который добавлял подсписок в пустой список. Следующий добавляется ко всем подспискам. Внутренний цикл for определил, что число внутри треугольника является суммой соседней строки выше. В конце концов, мы использовали цикл for для печати треугольника Паскаля в соответствии с форматом.

Способ 2

Мы можем использовать другой метод, следуя биномиальному коэффициенту, вся строка начинается с 1, а i-я запись в строке номера строки – это биномиальный коэффициент C(строка, i). Формула приведена ниже.

Временная сложность указанного выше метода равна 0(N2).

Способ 3

Этот метод является оптимизированным способом печати треугольника Паскаля. Этот метод основан на степени 11.

Как мы можем видеть в приведенном выше коде, когда мы вводим количество строк пять. Это дало неверный результат. Это означает, что он работает только до n