Kd и mc хорды одной окружности причем e точка

Геометрия | 10 — 11 классы

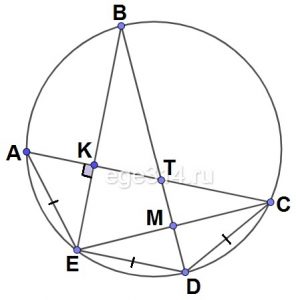
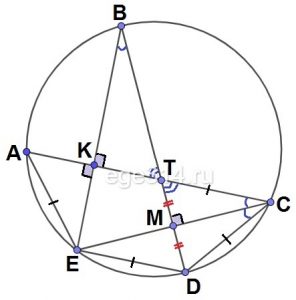
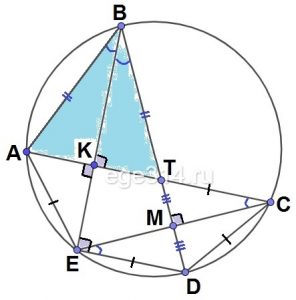
KD и MC — хорды одной окружности, причём Е — точка их пересечения .

Найдите угол CDE , если угол DEM в 4 раза больше DEC , а угол CMK на 26 градусов больше угла DEC .

Решение во вложении

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Дано : AC и BD — хорды одной окружности, причем E — точка их пересечения?

Дано : AC и BD — хорды одной окружности, причем E — точка их пересечения.

Угол CED в 9 раз больше угла DEC, а угол DAE на 61градус больше угла DEC.

Найдите угос CBE.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

В треугольнике CDE угол D в 4, 5 раза больше угла С, а угол Е на 20 градусов больше угла D?

В треугольнике CDE угол D в 4, 5 раза больше угла С, а угол Е на 20 градусов больше угла D.

Найдите углы треугольника.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

В треугольнике CDE угол C в 4, 5 раза меньше угла D, а угол E на 20 градусов больше угла D?

В треугольнике CDE угол C в 4, 5 раза меньше угла D, а угол E на 20 градусов больше угла D.

Найдите углы треугольника.

Видео:Окружность, касательная, секущая и хорда | МатематикаСкачать

В треугольнике CDE угол D в 2, 5 раза больше угла C , а угол E на 24 градуса меньше угла D ?

В треугольнике CDE угол D в 2, 5 раза больше угла C , а угол E на 24 градуса меньше угла D .

Видео:Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

О — точка пересечения биссектрис углов С и D в треугольнике CDE?

О — точка пересечения биссектрис углов С и D в треугольнике CDE.

Угол С = 54 * , угол D = 94 * Найдите угол C1OD1.

Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

На продолжении стороны АDпаралелограмма ABCD за точкой D отмечена точка Е так, чтоСD = DE?

На продолжении стороны АDпаралелограмма ABCD за точкой D отмечена точка Е так, чтоСD = DE.

Найдите больший угол параллелограмма ABCD, если угол DEC = 53 градуса.

Видео:№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

О — точка пересечения биссектрис углов С и Д в треугольнике СДЕ?

О — точка пересечения биссектрис углов С и Д в треугольнике СДЕ.

Угол С = 54 градуса, угол Д = 94 градуса.

Найдите угол С1ОД1.

Видео:Условие принадлежности четырёх точек одной окружностиСкачать

Определи величины углов равнобедренного треугольника DEC, если внешний угол угла D при основании DC равен 114°?

Определи величины углов равнобедренного треугольника DEC, если внешний угол угла D при основании DC равен 114°.

Надо найти угол каждого угла помогите быстро надо.

Видео:Угол между хордой и касательной. 9 класс.Скачать

На продолжении стороны АD параллелограмма АВСD за точкой D отмечена точка Е так , что DC = DE?

На продолжении стороны АD параллелограмма АВСD за точкой D отмечена точка Е так , что DC = DE.

Н найдите больший угол параллелограмма ABCD , если угол DEC = 53°.

Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Дан равнобедренный треугольник ABC с основанием AC?

Дан равнобедренный треугольник ABC с основанием AC.

На сторонах AB и AC поставлены точки D и E , чтобы DE || AC.

Найдите угол BDE и угол DEC , если угол C = 48 градусов!

На этой странице сайта, в категории Геометрия размещен ответ на вопрос KD и MC — хорды одной окружности, причём Е — точка их пересечения ?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Сумма углов треугольника 180° 5 : 1 : 3 Т. Е. всего частей 5 + 1 + 3 = 9 частей 180° : 9 = 20° одна часть Углы треугольника соотносятся как 5 * 20° : 20° : 20° * 3 100° : 20° : 60°.

Cos B = Bc AB = 8 10 = 0. 8.

Полупериметр (сумма двух сторон) равен 16 / 2 = 8 см ; 3х + 5х = 8 х = 1 см — одна часть длины стороны ; 1 * 3 = 3 см — одна пара сторон ; 1 * 5 = 5 см — другая пара сторон.

Держи) я полагаю, достаточно подробно.

X — y = 12x * y = — 32x = 12 + yx = — 32 / y12 + y = — 32 / yотсюда y = — 4тогда x = 8.

1)Средняя линия трапеции равна полусумме оснований = > (ВС + АD) / 2 = 10 ВС + АD = 20 — сумма оснований 2)36 — 20 = 16 — 2 боковые стороны, а т. К. трапеция равнобедренная, то 16 : 2 = 8 — одна боковая сторона Ответ : 8см.

Извини я не знаю этот язык (.

1. вид треугольника невозможно определить. 2. ответ : 123°.

АВСD — параллелограмм, зн. АВ = CD. Рассмотрим треугольники АВD и BDC : AB = CD, BD — общая, угол ABD = углуСDВ (по рисунку). Значит по двум сторонам и углу между ними (1 — ый признак равенства треугольников) треугольники равны. Ч. т. Д. .

Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм. Значит, АВ = ДС, диагональ ВД — общая сторона этих тре — ков, углы равны (на черт обозначены), след — но тре — ки равны по ..

Видео:Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать

Kd и mc хорды одной окружности причем e точка

Вопрос по геометрии:

KD и MC — хорды одной окружности, причём Е -точка их пересечения . Найдите угол CDE , если угол DEM в 4 раза больше DEC , а угол CMK на 26 градусов больше угла DEC .

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

решение во вложении
_______________________

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:11 класс, 40 урок, Угол между касательной и хордойСкачать

Kd и mc хорды одной окружности причем

Видео:Радиус и диаметрСкачать

Kd и mc хорды одной окружности причем

Вопрос по геометрии:

KD и MC — хорды одной окружности, причём Е -точка их пересечения . Найдите угол CDE , если угол DEM в 4 раза больше DEC , а угол CMK на 26 градусов больше угла DEC .

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

решение во вложении
_______________________

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Kd и mc хорды одной окружности причем

БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3

3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3

4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности.
б) Найдите A₁ H, если BC = 2√3.

5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10

6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4

7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6

8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.

9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.

11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88

12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.

13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.

14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .}

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65

18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4

19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .

б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2

20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3

21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1

22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36

23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4

24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.

25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.

26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.

28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.

Видео:№666. Хорды АВ и CD пересекаются в точке Е. Найдите ED, если: а) АЕ = 5, ВЕСкачать

Решение №2311 Точки A, B, C, D и E лежат на окружности в указанном порядке, причем AE = ED = CD, а прямые AC и BE перпендикулярны.

Точки A, B, C, D и E лежат на окружности в указанном порядке, причем AE = ED = CD, а прямые AC и BE перпендикулярны. Отрезки AC и BD пересекаются в точке T.

а) Докажите, что прямая EC пересекает отрезок TD в его середине.
б) Найдите площадь треугольника ABT, если BD = 6, АЕ = sqrt .

Источник: Ященко ЕГЭ 2022 (36 вар)

AE = ED = CD, AC⊥BE, Т – точка пересечения АС и ВD.
Обозначим: К – точка пересечения АС и ВЕ, М – точка пересечения СЕ и DT.

а) Доказать: DM = МТ .

∠ЕВК = ∠АСЕ = ∠ECD = ∠CED = ∠α – как вписанные углы окружности опирающиеся на равные дуги ‿ED = ‿AE = ‿CD (равны хорды стягивающие дуги).
Т.к. AC⊥BE, то ∠ВКТ = 90°.
Рассмотрим ΔКВТ и ΔТСМ, в них ∠КТВ = ∠СТМ – вертикальные, ∠КВТ = TCM – совпадающие с вписанными углами. Сумма углов в треугольнике равна 180°, значит и третьи углы равны ∠ВКТ = ∠ТМС = 90°.
В ΔТСD МС является медианой и высотой, значит треугольник равнобедренный, МС медиана, тогда DM = МТ.
Что и требовалось доказать.

б) ВD = 6, АЕ = sqrt . Найти: S_ΔАВТ .

В ΔАВТ ВК биссектриса (∠АВЕ = ∠КВТ, как совпадающие с вписанными опирающимися на равные дуги) и высота (∠ВКТ = 90°), значит и медиана, треугольник равнобедренный, боковые стороны равны АВ = ВТ.
Площадь ΔАВТ будем искать как половину произведения его сторон на синус угла между ними:

Прямая ЕС пересекает прямые АС и ЕD, образованные накрест лежащие углы равны ∠АСЕ = ∠СЕD (как вписанные опирающиеся на равные дуги), значит АС||ED. КЕ секущая к этим же прямым, накрест лежащие углы равны ∠АКЕ = ∠КЕD = 90°.
Треугольник ВЕD – прямоугольный (∠КЕD = 90°) вписан в окружность, значит его гипотенуза является диаметром окружности D = 2R = BD = 6.
По теореме синусов найдём sin α :

Найдём cos α :

cos 2 α + sin 2 α = 1

Найдём sin∠AВТ = sin 2α (∠AВТ = ∠АВК + ∠КВТ = α + α = 2α):

ТС = DC = AE = sqrt . Из прямоугольного ΔМТС найдём МТ:

6·MT = sqrt · sqrt
6·MT = 6
MT = 1

Найдём DT:

DT = 2·МТ = 2·1 = 2

Найдём ВТ = ВА:

ВТ = ВА = BD – DT = 6 – 2 = 4

Найдём площадь треугольника АВТ:

S_ =frac cdot ABcdot BTcdot sin angle ABT=frac cdot 4cdot 4cdot frac > =frac >

🎬 Видео

Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Угол между касательной и хордойСкачать

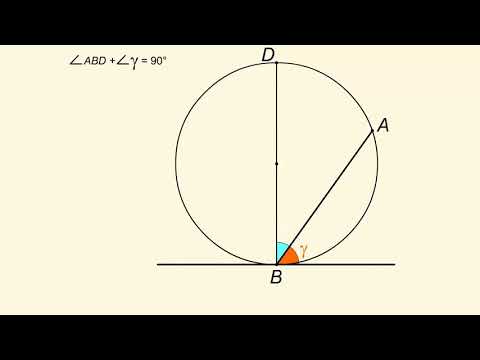
Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Угол между касательной и хордой | Задачи 1-10 | Решение задач | Волчкевич|Уроки геометрии 7-8 классыСкачать

Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать