Касательные к окружности образуют угол 122

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Ваш ответ

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

решение вопроса

Видео:ЕГЭ Математика Задание 6#27880Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,909
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Касательные к окружности образуют угол 122

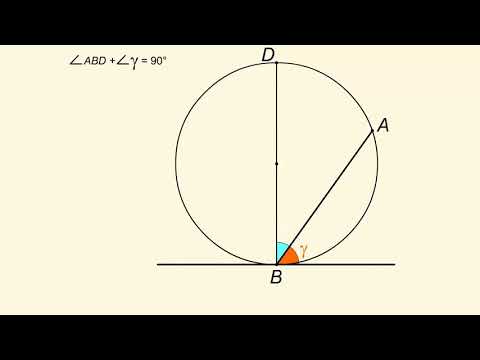
Касательные CA и CB к окружности образуют угол ACB, равный 122°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Треугольник АВС равнобедренный, так как отрезки касательных, проведенных к окружности из одной точки, равны. Следовательно, угол ВAC равен 0,5(180° − 122°) = 29°. Угол между касательной и хордой, проведенной через точку касания, равен половине заключенной между ними дуги, поэтому искомая дуга равна 2 · 29° = 58°.

Приведем другое решение.

Пусть искомая длина меньшей дуги АВ равна х, тогда длина большей дуги АВ равна 360° − х. Угол между двумя касательными, проведенными из одной точки, равен половине высекаемых ими дуг, откуда имеем: 0,5(360° − 2x) = 122°. Тогда x = 58°.

Видео:ЗАДАНИЕ 1 ЕГЭ (ПРОФИЛЬ). ХОРДА, КАСАТЕЛЬНАЯ И СЕКУЩАЯ.Скачать

Презентация по математике на отработку навыков решения задач ГИА по теме «Окружность»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Углы с вершинами внутри и вне круга <

Теорема 1 Угол между двумя пересекающимися хордами измеряется полусуммой заключенных между ними дуг..

Теорема 2 Угол между двумя секущими, проведенными из одной точки, измеряется полуразностью заключенных внутри него дуг.

Теорема 3 Угол между касательной и секущей, проведенными из одной точки, измеряется полуразностью заключенных внутри него дуг.

Теорема 4 Угол между двумя касательными, проведенными из одной точки, равен 180° минус величина заключенной внутри него дуги, меньшей полуокружности

Упражнение 1 Вписанные углы ACB и CAD равны соответственно 36о и 20о. Найдите угол AQB, образованный пересекающимися хордами AC и BD. Ответ: 56о.

Упражнение 2 Угол AQB, образованный пересекающимися хордами AC и BD окружности, равен 54о. Вписанный угол ACB равен 34о. Найдите вписанный угол CAD. Ответ: 20о.

Упражнение 3 Дуги AB и CD окружности составляют соответственно 72о и 38о. Найдите угол AQB, образованный пересекающимися хордами AC и BD. Ответ: 55о.

Упражнение 4 Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 118о и 38о. Ответ: 40о.

Упражнение 5 Угол ACB равен 42о. Градусная величина дуги AB окружности равна 124о. Найдите угол DAE. Ответ: 40о.

Упражнение 6 Угол ACB равен 42о. Градусная величина дуги DE окружности равна 38о. Найдите угол ADB. Ответ: 61о.

Упражнение 7 Найдите угол ACB, если вписанный угол ADB равен 62о, а угол AQB равен 80о. Ответ: 44о.

Упражнение 8 Хорда AB стягивает дугу окружности в 92о. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ: 46о.

Упражнение 9 Угол между хордой AB и касательной BC к окружности равен 32о. Найдите градусную величину дуги, стягиваемую хордой AB. Ответ: 64о.

Упражнение 10 Через концы A, B дуги окружности в 62о проведены касательные AC и BC. Найдите угол ACB. Ответ: 118о.

Упражнение 11 Касательные CA и CB к окружности образуют угол ACB, равный 122о. Найдите градусную величину дуги AB, стягиваемую точками касания. Ответ: 58о.

Упражнение 12 Хорда АВ стягивает дугу окружности в 44о. Найдите углы, которые образует эта хорда с касательными к окружности, проведенными через ее концы. Ответ: 22о.

Упражнение 13 Найдите угол ACB, если его стороны CA и CB касаются окружности, а дуга ADB окружности, заключенная внутри этого угла, равна 132о. Ответ: 48о.

Упражнение 14 Угол ACB равен 52о. Его стороны CA и CB касаются окружности. Найдите градусную величину дуги ADB окружности, заключенной внутри этого угла. Ответ: 128о.

Упражнение 15 Найдите угол ACB, если его стороны CA и CB касаются окружности, а дуга ADB окружности, заключенная внутри этого угла, равна 232о. Ответ: 52о.

Упражнение 16 Угол ACB равен 48о. Его стороны CA и CB касаются окружности. Найдите градусную величину дуги ADB окружности, заключенной внутри этого угла. Ответ: 228о.

Упражнение 17 В угол АВС вписана окружность. Точки касания делят окружность на дуги, градусные величины которых относятся как 5:4. Найдите величину угла АВС. Ответ: 20о.

Упражнение 18 Окружность разделена точками А, В, С на дуги, градусные величины которых относятся как 11 : 3 : 4. Через точки А, В, С проведены касательные до их взаимного пересечения. Найдите углы образовавшегося треугольника. Ответ: 80о, 60о, 40о.

Упражнение 19 Найдите величину угла ACB. Ответ: 45о.

Упражнение 20 Найдите величину угла ACB. Ответ: 45о.

Упражнение 21 Найдите геометрическое место точек, из которых данный отрезок АВ виден под данным углом, т. е. таких точек С, для которых угол АСВ равен данному углу.

Упражнение 22 Найдите геометрическое место вершин C прямоугольных треугольников АВС с данной гипотенузой АB.

Упражнение 23 Ответ: а) ГМТ, лежащих вне окружности с диаметром AB и не принадлежащих прямой AB; Для данных точек А и В найдите геометрическое место точек С, для которых угол АСВ: а) острый; б) тупой.

Упражнение 24 На прямой c отметьте точку C, из которой отрезок AB виден под наибольшим углом.

Упражнение 25 На прямой c отметьте точку C, из которой отрезок AB виден под наибольшим углом.

Упражнение 26 В треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы A1AC и B1BC равны. Для доказательства равенства углов можно было бы воспользоваться тем, что стороны данных углов перпендикулярны.

Упражнение 27 В треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы AA1B1 и ABB1 равны.

Упражнение 28 В треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы BAC и B1A1C равны. Доказательство. Угол BAC равен 90о минус угол ABB1. Угол B1A1C равен 90о минус угол AA1B1. Так как углы AA1B1 и ABB1 равны (см. предыдущую задачу), то равны и углы BAC и B1A1C.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 944 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 318 человек из 68 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 694 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 485 611 материалов в базе

Видео:#59. Олимпиадная задача о касательной к окружности!Скачать

Дистанционные курсы для педагогов

Другие материалы

• 26.09.2015
• 1983

• 26.09.2015
• 14156

• 26.09.2015
• 804

• 26.09.2015
• 11099

• 26.09.2015
• 1966

• 26.09.2015
• 679

• 26.09.2015
• 663

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 26.09.2015 5375 —> —> —> —>
• PPTX 4.1 мбайт —> —>
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Викторова Елена Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 11654
• Всего материалов: 6

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Построение касательной к окружностиСкачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Число иностранных студентов в РФ увеличилось за три года

Время чтения: 1 минута

Ускоренный просмотр онлайн-лекций не мешает их пониманию

Время чтения: 3 минуты

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📹 Видео

Угол между хордой и касательной. 9 класс.Скачать

Секретная теорема из учебника геометрииСкачать

Окружность, касательная, секущая и хорда | МатематикаСкачать

Касательные к окружностиСкачать

Построение касательной к окружности.Скачать

Углы, связанные с окружностьюСкачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

ВЕБИНАР № 2. Планиметрия. Касательная к окружности.Скачать

Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Угол между касательной и хордойСкачать