Касательная окружности вписанной в треугольник abc пересекает стороны

Видео:Решение задачи №1 из ЕГЭ математикаСкачать

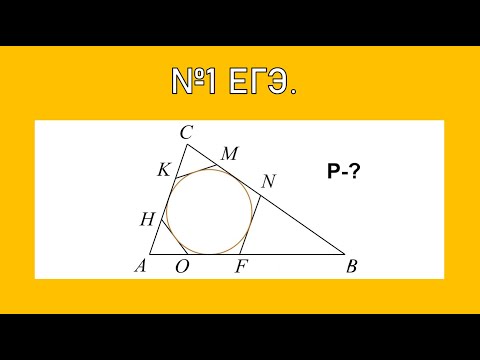
Условие

К окружности, вписанной в правильный треугольник ABC , проведена касательная, пересекающая стороны AC и BC в точках M и N соответственно и касающаяся окружности в точке T .

а) Докажите, что периметр треугольника MNC равен стороне треугольника ABC .

б) Найдите MT:TN, если известно, что CM: MA=1:4.

Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Решение

а) Пусть K и L — точки касания окружности и сторон BC и AC соответственно.

Так как MT=ML и NK=NT как отрезки касательных, проведенных из одной точки, то

P_= CM+MT+TN+NC= CM+ML+KN+NC= CL+KC.

Так как ABC — правильный треугольник, то CL=KC=frac. Следовательно, P_=AC, что и требовалось доказать.

б) 1 . Обозначим TN=x, CM=a. Так как CM:MA=1:4 по условию, то MA=4a и AC=5a.

Тогда CL=frac=fraca и ML=CL-CM=fraca-a=fraca. Так как ML=MT, то MT=fraca. Тогда MN=MT+TN=fraca+x.

Так как NT=NK, то NK=x. Тогда CN=CK-NK=frac-x=fraca-x.

2. По теореме косинусов для треугольника MNC

MN^2=CN^2+CM^2- 2 cdot CN cdot CM cdot cos angle NCM. Подставляя в это уравнение выражения для сторон треугольника MNC , получим:

left ( fraca+xright )^2= left ( fraca-xright )^2+a^2-2left ( fraca-xright )a cos 60^circ;

fraca^2+2 cdot fracax+x^2= fraca^2-2 cdot fracax+x^2+a^2- 2left ( fraca-x right )a cdot frac;

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

КАСАТЕЛЬНАЯ К ОКРУжНОСТИ , ВПИСАННОЙ В ТРЕУГОЛЬНИК ABC ПЕРЕСЕКАЕТ СТОРОНЫ ВС

КАСАТЕЛЬНАЯ К ОКРУжНОСТИ , ВПИСАННОЙ В ТРЕУГОЛЬНИК ABC ПЕРЕСЕКАЕТ СТОРОНЫ ВС И АС СООТВЕТСТВЕННО В ТОЧКАХ А1 И В1 . НАЙДИТЕ ПЕРИМЕТР ТРЕУГОЛЬНИКА А1В1С1 ЕСЛИ ВС =5, АС=6 И АВ=7

МОЖНО ТОЛЬКО ОТВЕТ БЕЗ РЕШЕНИЯ!

• Мирослава Вахрущева
• Геометрия 2018-12-16 16:06:54 4 1

Ответ без решения 4 :))))))))))))

Да хорошо, напишу решение.

По свойству отрезков касательных из одной точки сходу ясно, что периметр А1В1С (без 1) равен УДВОЕННОМУ отрезку от верхушки С до точки касания АС с вписанной окружностью. Это на самом деле теснее ВСЁ решение, но я продолжу :))

Надобно отыскать r — вписанной окружности и угол С (поточнее, надобно отыскать ctg(C/2));

По формуле Герона считаем площадь треугольника, она одинакова 6* 6; полупериметр 9; отсюда r = 2* 6/3;

по аксиоме косинусов

7^2 = 5^2 + 6^2 — 2*5*6*cos(C); откуда cos(C) = 1/5; ctg(C/2) = 6/2;

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно?

Геометрия | 5 — 9 классы

К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно.

Известно, что AB = 33, а периметр треугольника ABC равен 103.

НАйти периметр треугольника CPQ.

Нашел чему равно PQ.

К. PN = PK и KQ = QM (по свойству касательных), то СN + CM = P треуг.

AN = AL и MB = BL, то AN + NB = AB (по св — ву касательных)

ABC = AB + BC + AC, где BC = CM + MB ; AC = CN + AN

Получим : AB + CM + MB + CN + AN = 103 (выделенные величины равно, поэтому их складываем)

AB + 2CM + MB + AN = 103 (см.

Отсюда CM = 51, 5 — 33 = 18, 5

CN + CM = P треуг.

СPQ и CN = CM (по св — ву касат.

CPQ = 2CM = 2 * 18, 5 = 37.

Видео:Геометрия К окружности, вписанной в треугольник ABC, проведены три касательные (см. рис.)Скачать

Через середину P стороны AB треугольника ABC проведена прямая, параллельная стороне AC и пересекающая сторону BC в точке Q?

Через середину P стороны AB треугольника ABC проведена прямая, параллельная стороне AC и пересекающая сторону BC в точке Q.

Найдите длину стороны AC, если известно, что периметр треугольника ABC равен 54см, QC = 12см, а PQ в два раза больше, чем BP.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

КАСАТЕЛЬНАЯ К ОКРУжНОСТИ , ВПИСАННОЙ В ТРЕУГОЛЬНИК ABC ПЕРЕСЕКАЕТ СТОРОНЫ ВС И АС СООТВЕТСТВЕННО В ТОЧКАХ А1 И В1 ?

КАСАТЕЛЬНАЯ К ОКРУжНОСТИ , ВПИСАННОЙ В ТРЕУГОЛЬНИК ABC ПЕРЕСЕКАЕТ СТОРОНЫ ВС И АС СООТВЕТСТВЕННО В ТОЧКАХ А1 И В1 .

НАЙДИТЕ ПЕРИМЕТР ТРЕУГОЛЬНИКА А1В1С1 ЕСЛИ ВС = 5, АС = 6 И АВ = 7 МОЖНО ТОЛЬКО ОТВЕТ БЕЗ РЕШЕНИЯ!

Видео:ЕГЭ по математике. Задание №16 #11Скачать

Периметр треугольника ABC равен 8?

Периметр треугольника ABC равен 8.

В треугольник вписана окружность и к ней проведена касательная, параллельная стороне AB.

Отрезок этой касательной, заключённый между сторонами AC и CB, равен 1.

Найдите сторону AB.

Видео:✓ Простое решение красивой геометрии | Планиметрия | Физтех-2021. Математика | Борис ТрушинСкачать

В равнобедренный треугольник ABC вписана окружность, касающаяся боковых сторон треугольника в точках K и E?

В равнобедренный треугольник ABC вписана окружность, касающаяся боковых сторон треугольника в точках K и E.

Найдите периметр треугольника ABC, если хорда KE равна 12 см, а отрезок касательной, заключенной между боковыми сторонами и параллельный основанию, равен 10 см.

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Периметр треугольника ABC равен 12см, а длина диаметра окружности , вписанной в него , равна 6 см?

Периметр треугольника ABC равен 12см, а длина диаметра окружности , вписанной в него , равна 6 см.

Вычислите площадь треугольника ABC.

Видео:Задание 26 Две окружности, внешнее касаниеСкачать

Периметр треугольника abc равен 12 окружность касающаяся стороны AB и продолжение сторон AC и BC касается прямой АС в точке Р?

Периметр треугольника abc равен 12 окружность касающаяся стороны AB и продолжение сторон AC и BC касается прямой АС в точке Р.

К этой окружности проведена касательная параллельная прямой AB и пересекающая продолжение сторон АС и ВС в точках M и N так что MN = 3 НАйдите длину отрезка PQ где Q точка касания вписаной окружности треугольника ABC со стороной AC.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

К окружнности, вписанной в треугольник ABC, проведены три касательные?

К окружнности, вписанной в треугольник ABC, проведены три касательные.

Периметры отсеченных треугольников равны 10, 12, 7.

Найдите периметр данного треугольника.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Окружность радиуса 2, вписанная в треугольник ABC, касается средней линии треугольника, параллельной стороне BC?

Окружность радиуса 2, вписанная в треугольник ABC, касается средней линии треугольника, параллельной стороне BC.

Периметр треугольника ABC равен 24.

Найти стороны треугольника.

Видео:Планиметрия (№16) из работы Статград от 30 марта 2023 года (МА2210409)Скачать

Точки T и O — соответственно середины AB и BC треугольника ABC?

Точки T и O — соответственно середины AB и BC треугольника ABC.

В треугольник BTO вписана окружность.

Вычислите длину радиуса окружности, если известно, что площадь треугольника TBO равна 12 см², а периметр треугольника ABC равен 16.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Треугольник ABC – равносторонний?

Треугольник ABC – равносторонний.

Окружность, вписанная в этот треугольник, касается его сторон в точках M и N .

Длина дуги этой окружности равна 1.

Какой периметр имеет треугольник ABC?

На странице вопроса К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

🌟 Видео

ОГЭ по математике. Задача 26Скачать

Задание 26 Свойство касательной и секущей Подобные треугольникиСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

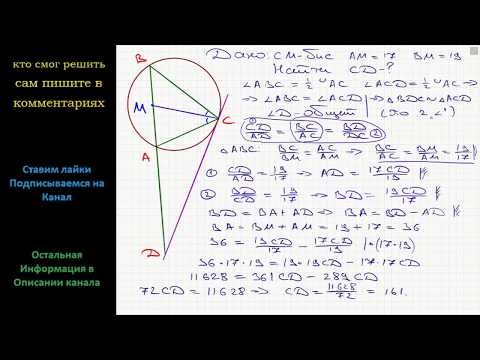
Геометрия Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 17 и MB = 19. КасательнаяСкачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать