Построение касательных к двум окружностям
При вычерчивании контуров предметов сравнительно часто приходится строить общие касательные к двум дугам окружностей. Общая касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон касательной.
Построение общей внешней касательной к двум окружностям радиусов R и r (рис. 180). Из центра окружности большего радиуса – точки O1 описывают окружность радиусом R – r (рис 180 а). Находят середину отрезка O2O1 – точку O3 и из нее проводят вспомогательную окружность радиусом O3O2 или O3O1. Обе проведенные окружности пересекаются в точках A и В. Точки O1 и B соединяют прямой и в пересечении ее с окружностью радиуса R определяют точку касания D (рис. 180 б). Из точки O2 параллельно прямой O1D проводят линию до пересечения с окружностью радиуса r и получают вторую точку касания C. Прямая CD является искомой касательной. Так же строится вторая общая внешняя касательная к этим окружностям (прямая EF).
Построение общей внутренней касательной к двум окружностями радиусов R и r (рис. 48). Из центра любой окружности, например: точки O1, описывают окружность радиусом R + r (рис. 181 а). Разделив отрезок O2O1 пополам, получают точку O3. Из точки O3, как из центра, описывают вторую вспомогательную окружность радиусом O3O2 = O3О1 и отмечают точки A и В пересечения вспомогательных окружностей. Соединив прямой точки A и O1 (рис. 181 б), в пересечении ее с окружностью радиуса R получают точку касания D. Через центр окружности радиуса r проводят прямую, параллельную прямой O1D, и в пересечении ее с заданной окружностью определяют вторую точку касания С. Прямая CD – внутренняя касательная к заданным окружностям. Аналогично строится и вторая касательная EF.
СОПРЯЖЕНИЯ С ПОМОЩЬЮ ДУГИ ОКРУЖНОСТИ
Сопряжение двух прямых дугой окружности
Все задачи на сопряжение дугой могут быть сведены к двум видам. Сопряжение осуществляется либо заданным радиусом сопрягающей дуги, либо через точку, заданную на одной из сопрягаемых линий. В том и другом случае необходимо построить центр сопрягающей дуги.
Сопряжение двух пересекающихся прямых дугой заданного радиуса Rc (рис. 182 а). Так как сопрягающая дуга должна касаться заданных прямых, то центр ее должен быть удален от каждой прямой на величину равную радиусу Rc. Сопряжение строят так. Проводят две прямые, параллельные заданным и удаленные от них на величину радиуса Rc и в пересечении этих прямых отмечают точку O – центр сопрягающей дуги. Из точки О опускают перпендикуляр на каждую из заданных прямых. Основания перпендикуляров – точки A и B – являются точками касания сопрягающей дуги. Такое построение сопряжения справедливо для двух пересекающихся прямых, составляющих любой угол. Для сопряжения сторон прямого угла можно воспользоваться также способом указанным на рисунке 182 б.
Сопряжение двух пересекающихся прямых, на одной из которых задана точка касания А сопрягающей дуги (рис. 183). Известно, что геометрическим местом центров дуг, сопрягающих две пересекающиеся прямые, является биссектриса угла, образованного этими прямыми. Поэтому построив биссектрису угла, из точки касания A восставляют перпендикуляр к прямой до пересечения его с биссектрисой и отмечают точку O – центр сопрягающей дуги. Опустив из точки О перпендикуляр на другую: прямую, получают вторую точку касания В и радиусом Rc = OA = OB осуществляют сопряжение двух прямых, на одной из которых была задана точка касания.
Сопряжение двух параллельных прямых дугой, проходящей через заданную точку касания А (рис. 183). Из точки A восставляют перпендикуляр к заданным прямым и на пересечении его со второй прямой отмечают точку B. Отрезок AB делят пополам и получают точку О – центр сопрягающей дуги радиуса .
Рис. 183 Рис. 184
Сопряжение дуги и прямой дугой окружности заданного радиуса
Могут встретиться два случая такого сопряжения: внешнее касание сопрягающей дуги с заданной и внутреннее касание. В обоих случаях задача сводится к определению центра сопрягающей дуги и точек касания.
При внешнем касании (рис. 185 а) из центра заданной дуги – точки O1 проводят вспомогательную дугу радиусом R + Rс. На расстоянии, равном радиусу Rc сопрягающей дуги, параллельно заданной прямой проводят прямую. Точка О пересечения вспомогательной дуги и прямой есть центр сопрягающей дуги. На пересечении прямой, соединяющей точки О и O1 с заданной дугой, отмечают точку касания A. Вторую точку касания В определяют как точку пересечения заданной прямой с перпендикуляром, опущенным на нее из точки О.
При внутреннем касании (рис. 185 б) определение центра сопрягающей дуги и точек касания аналогичны предыдущему случаю с той лишь разницей, что радиус вспомогательной дуги равен Rc – R,
Сопряжение двух дуг дугой окружности заданного радиуса
Различают три вида такого сопряжения:
1) внешнее сопряжение при внешнем касании сопрягающей дуги с двумя заданными;
2) внутреннее сопряжение при внутреннем касании сопрягающей дуги с двумя заданными;
3) смешанное сопряжение при внешнем касании сопрягающей дуги с одной заданной и внутреннем касании с другой.
При внешнем сопряжении (рис. 186 а) центр сопрягающей дуги точка O располагается в точке пересечения вспомогательных дуг радиусов r + Rc и R + Rc, проведенных соответственно из центров сопрягаемых дуг – точек O2 и O1. Точки касания A и B определяются как точки пересечения заданных дуг с прямыми OO1 и OO2.
Внутреннее сопряжение дуг радиусов r и R дугой радиус Rc показано на рисунке 186 б. Для определения центра сопрягающей дуги – точки О проводят вспомогательные дуги радиусами Rc – r и Rc – R соответственно из центров заданных дуг – точек O2 и O1. Точка О пересечения этих дуг и явится центром сопрягающей дуги. Из точки О через точки O1 и O2 проводят прямые до пересечения с заданными дугами и получают соответственно две точки касания – A и B.
При смешанном сопряжении центр сопрягающей дуги – точка О определяется как точка пересечения двух вспомогательных дуг радиусов Rc + R и Rс – r (рис. 186 в) или Rс – R и Rс + r, проведенных соответственно из центров заданных дуг – точек O1 и O2. Для определения точек касания сопрягающей дуги с заданными проводят две прямые: одну через точки О и O1, другую через точки О и O2. Точки пересечения каждой из них с заданными дугами дают искомые точки касания A и B.
Сопряжения Очертания многих предметов представляют собой сочетание ряда: линий, в большинстве своем плавно переходящих одна в другую. Примером плавных переходов могут служить контуры различных видов художественных изделий, посуды, рисунки орнаментов и т.п.
Вычерчивание контуров деталей Последовательность вычерчивания контуров деталей, в основном, зависит от их формы. Поэтому можно указать только на некоторые общие положения, справедливые для всех случаев.
Плоские кривые Кривые, у которых все точки расположены в одной плоскости, называют плоскими. Часть плоских кривых, состоящих из дуг окружностей, образует группу циркульных кривых. Дуги циркульных кривых касаются друг друга, поэтому построение их основано на правилах сопряжения и выполняется при помощи циркуля.
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Love Soft
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Навигация
- Связь
- Содержание
- Вписанный и центральный углы. Касательная
- Касательная
- Построение касательной
- Касательная к двум окружностям
- Касательные прямые и бильярд
- Угол между касательной и хордой
- Теорема о секущей и касательной
- Угол между секущими
- Свойства дуг, хорд и углов окружности
- 🎥 Видео
Видео:Внешняя касательная к двум окружностямСкачать
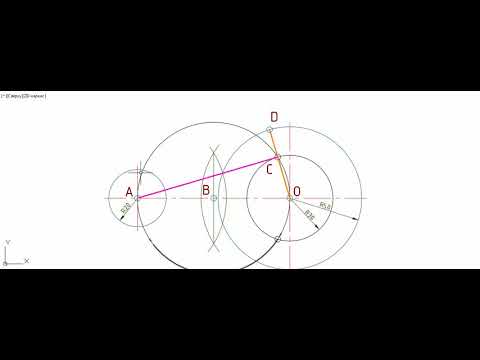
Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:Построение касательной к окружностиСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Построение касательной к окружности.Скачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать  Love SoftИнструменты пользователяИнструменты сайтаБоковая панельНавигация СвязьСодержаниеВидео:8 класс, 32 урок, Касательная к окружностиСкачать  Вписанный и центральный углы. КасательнаяУгловой мерой дуги окружности является величина центрального угла, опирающегося на эту дугу. Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается (по определению). Если провести два радиуса, то образуется два центральных угла (сумма которых 360°) и две дуги окружности (сумма длин которых 2πR). Большему центральному углу соответствует большая дуга. Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Когда говорят, что вписанный угол опирается на дугу — имеют в виду часть окружности, не содержащую вершину угла. Проще говоря, угол (и центральный и вписанный) опирается на ту дугу, которая принадлежит части плоскости между сторонами угла. Радианы — отношение длины s стягивающей дуги к её радиусу r. Таким образом, на единичной окружности величина центрального угла в радианах равна длине стягивающей дуги. Любой конкретной дуге окружности можно сопоставить единственный центральный и бесконечное множество вписанных углов. Теорема. Вписанный угол равен половине градусной меры дуги, на которую он опирается, или иначе говоря, равен половине центрального угла, опирающегося на ту же дугу. Следствия: Следствие из 2-го следствия: Гипотенуза прямоугольного треугольника является диаметром описанной около него окружности. Видео:1 2 4 сопряжение окружностейСкачать  КасательнаяКасательная прямая к окружности в евклидовой геометрии на плоскости — прямая, которая имеет с окружностью ровно одну общую точку. Также можно определить касательную как предельное положение секущей, когда точки пересечения её с окружностью бесконечно сближаются. англ Tangent line (танго — касаться)
Две секущие образуют угол, в который попадают две дуги окружности. В этом случае говорят, что секущие высекают эти дуги. Построение касательной
Соединить данную точку P и центр окружности O. На отрезке OP нужно «восстановить» прямоугольный треугольник. Воспользуемся тем, что если вписанный угол опирается на диаметр окружности, то этот угол прямой. Разделим отрезок OP пополам — получили точку H. Радиусом OH проводим еще одну окружность. Точка пересечения окружностей и есть точка касания. Касательная к двум окружностямОбщая касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон касательной.
Построение общей внешней касательной к двум окружностям радиусами R и r Из центра окружности большего радиуса – точки O1 описывают окружность радиусом R – r (рисунок 47, а). Находят середину отрезка O2O1 – точку O3 и из нее проводят вспомогательную окружность радиусом O3O2 или O3O1. Обе проведенные окружности пересекаются в точках A и В. Точки O1 и B соединяют прямой и в пересечении ее с окружностью радиусом R определяют точку касания D (рисунок 47, б). Из точки O2 параллельно прямой O1D проводят линию до пересечения с окружностью радиусом r и получают вторую точку касания C. Прямая CD является искомой касательной. Так же строится вторая общая внешняя касательная к этим окружностям (прямая EF). Построение общей внутренней касательной к двум окружностями радиусов R и r
Из центра любой окружности, например: точки O1, описывают окружность радиусом R + r (рисунок 48, а). Разделив отрезок O2O1 пополам, получают точку O3. Из точки O3 как из центра описывают вторую вспомогательную окружность радиусом O3O2 = O3О1 и отмечают точки A и В пересечения вспомогательных окружностей. Соединив прямой точки A и O1 (рисунок 48, б), в пересечении ее с окружностью радиуса R получают точку касания D. Через центр окружности радиуса r проводят прямую, параллельную прямой O1D, и в пересечении ее с заданной окружностью определяют вторую точку касания С. Прямая CD – внутренняя касательная к заданным окружностям. Аналогично строится и вторая касательная EF. Касательные прямые и бильярдСистема касательных прямых прицеливания битка использует прямую, проходящую через середину кия, для создания двух касательных прямых от битка в направлении прицельного шара. Две касательные прямые и прямая через середину битка пересекают прямую, проходящую через середину прицельного шара и центр лузы. Необходимо направить удар так, чтобы конечное положение битка (воображаемый шар на рисунке) касалось прицельного шара в точке касания прямой, перпендикулярной направлению на лузу (на рисунке эта касательная выделена зелёным цветом).
Видео:Касательные к окружностиСкачать  Угол между касательной и хордойУгол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Угол между касательной и хордой является вырожденным случаем вписанного угла, в котором вершина угла совпадает с одним из концов дуги. Касательная перпендикулярна радиусу, проведенному в точку касания. Пусть $angle MCA=varphi$. Тогда $angle OCA = 90 ^-varphi$. Треугольник $OCA$ – равнобедренный, $OA = OC$ (как радиусы окружности). Значит, $angle AOC= 180 ^-2left ( 90 ^ — varphi right )=2varphi$, что и требовалось доказать. Заметим, что $angle ABC = varphi$ – как вписанный, опирающийся на ту же дугу.
Видео:Построение внутренней касательной к двум дугам окружностей.Урок12.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  Теорема о секущей и касательнойКвадрат отрезка касательной равен произведению длин отрезков секущей. Квадрат касательной равен произведению секущей на ее внешнюю часть.
Мысленно сближать точки пересечения секущей с окружностью: тогда PN будет стремиться к PT с одной стороны, а PM — с другой стороны, а произведение их длин будет стремиться к $PT^2$ Доказательство следует из подобия треугольников PMT и PTN https://i.imgur.com/C5EMn1t.jpg Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать  Угол между секущимиЕсли точка пересечения двух секущих к окружности находится внутри окружности, то угол между секущими равен полусумме дуг, которые они высекают. Если точка пересечения двух секущих к окружности находится вне окружности, то угол между секущими равен половине разности дуг, которые они высекают.
Теорема выполняется, если заменить секущую на касательную к окружности. Видео:Секретная теорема из учебника геометрииСкачать  Свойства дуг, хорд и углов окружности
🎥 ВидеоВсё про углы в окружности. Геометрия | МатематикаСкачать  Касательная к двум окружностям разного диаметра.3 часть.Скачать  Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать  Угол между хордой и касательной. 9 класс.Скачать 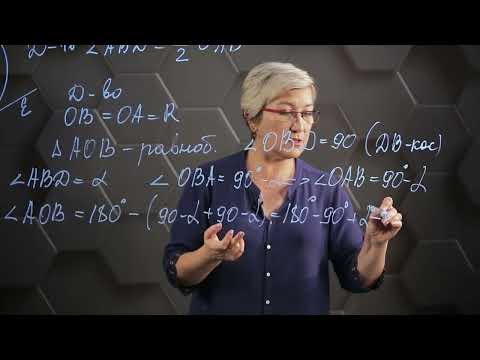 Строим касательную к окружности (Задача 3).Скачать  Сопряжение двух окружностей по касательной прямойСкачать  Взаимное расположение окружностей. 7 класс.Скачать  Внутренняя касательная к двум окружностямСкачать  Секущая и касательная. 9 класс.Скачать  |
Загрузки всякие
Доказательство. Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство α = π – γ. Далее получаем γ = 2π — β, значит, α = β — π. Складываем два выражения для α и делим пополам. α = (β-γ)/2