Касательная к описанной окружности треугольника klm проходящая через точку k

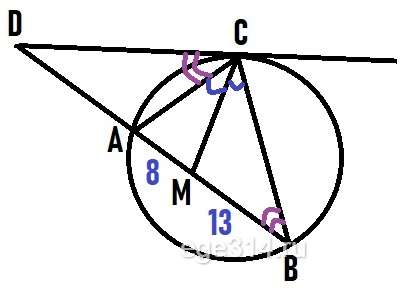
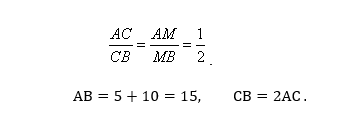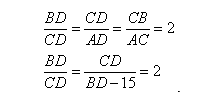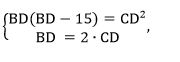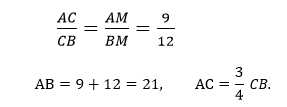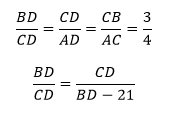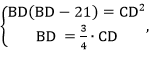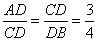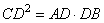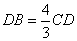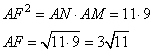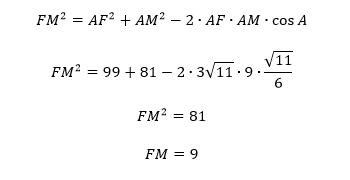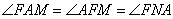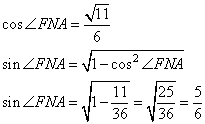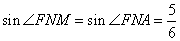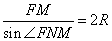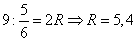Биссектриса СМ треугольника АВС делит сторону АВ на отрезки АМ = 8 и МВ = 13. Касательная к окружности, описанной около треугольника АВС, проходит через точку С и пересекает прямую АВ в точке D. Найдите СD.

CM – биссектриса, то по свойству биссектрисы:

Рассмотрим ΔDAC и ΔDBC, в них ∠D общий, ∠В вписанный, значит равен половине дуги на которую опирается:

∠В = ‿АС

∠DCA угол между касательной и хордой, равен половине дуги заключённой между ними:

∠DCA = ‿АС
∠В = ∠DCA

ΔDAC ∼ ΔDBC подобны по двум углам, отсюда получаем отношение для трёх сторон:

Выразим DA:

Всё подставим и найдём СD:

Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Ваш ответ

Видео:#3warmup. Разбор третьей разминкиСкачать

решение вопроса

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Похожие вопросы

• Все категории
• экономические 43,283
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,073
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Задание №26 ОГЭ по математике

Видео:Касательная к графику функции в точке. 10 класс.Скачать

Комплексная геометрическая задача

Разбор типовых вариантов заданий №26 ОГЭ по математике

Первый вариант задания

Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 5 и MB =10. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD.

Алгоритм решения:

1. Делаем чертеж.
2. Определяем равенство угла между касательной и хордой и угла АВС.
3. Определяем соотношение отрезков из свойства биссектрисы угла треугольника и найдем АВ.
4. Показываем, что треугольники DAC и DCB подобны.
5. Составляем соотношения сторон подобных треугольников.
6. Составляем систему равенств.
7. Решаем систему.
8. Записываем ответ.

Решение:

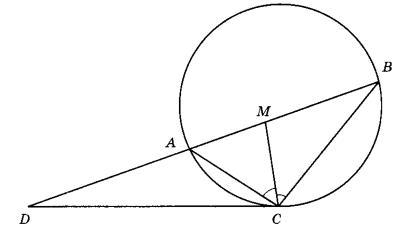
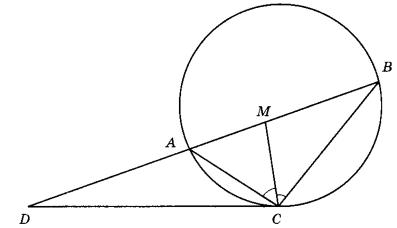
1. Выполняем чертеж данной задачи:

2. Рассматриваем АСD. В нем:

Согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,

4. Рассмотрим DAC и DCB. У них:

∠ DCA = ∠ DBC по доказанному выше,

Следовательно, DAC DCB по двум углам.

5. Из определения и свойств подобных треугольников имеем:

6. Составим систему равенств:

7. Решим систему:

Второй вариант задания

Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 9 и MB = 12. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD.

Алгоритм решения:

1. Сделаем чертеж.
2. Определим равенство углов CDB и АВС.
3. Определим соотношение отрезков, воспользовавшись свойством биссектрисы угла треугольника, и определим длину АВ.
4. Покажем, что треугольники DAC и DCB подобны.
5. Составим соотношения сторон подобных треугольников.
6. Составим систему равенств.
7. Решим систему.
8. Запишем ответ.

Решение:

1. Делаем чертеж.

2. Рассмотрим АСD. В нем, согласно свойству углов окружности, касательной и секущей,
угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла.
⇒∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, согласно которому она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,

4. Рассмотрим DAC и DCB. У них:

∠ DCA = ∠ DBC по доказанному выше,

Значит, DAC DCB по двум углам.

5. Из определения и свойств подобных треугольников имеем:

6. Составим систему равенств:

7. Решим систему:

Так как AD = DB-21, имеем:

Таким образом, искомая длина CD=36.

Четвертый вариант задания

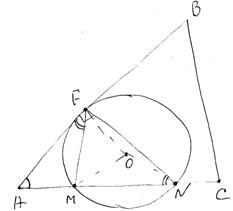
Точки М и N лежат на стороне АС треугольника ABC на расстояниях соответственно 9 и 11 от вершины А. Найдите радиус окружности, проходящей через точки М и N и касающейся луча АВ, если cos ∠BAC = √11 / 6

Алгоритм решения:

1. Сделаем чертеж.
2. Установим подобие треугольников AFM и ANF.
3. Определим сторону FM.
4. Определим ∠FNA.
5. Найдем .
6. Составим теорему синусов и найдем радиус окружности.
7. Запишем ответ.

Решение:

1. Рассмотрим треугольники AFM и ANF. У них:

Угол A является общим, а

по доказанному выше.

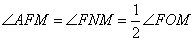
Следовательно, треугольник AFM подобен треугольнику ANF по двум углам. Отсюда вытекает:

3. В треугольнике AFM сторона AF=3, сторона AM=9. Воспользуемся теоремой косинусов для определения FM:

Полученное значение означает, что AFM является равнобедренным. У него основание AF.

4. По свойству равнобедренного треугольника ∠FAM=∠AFM. Отсюда

6. Из FMN по теореме синусов:

где R – радиус описанной окружности.

Отсюда получим значение радиуса окружности:

Демонстрационный вариант ОГЭ 2019

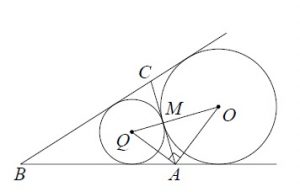
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC .

Решение:

Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC .

Точка касания M окружностей делит AC пополам по условию.

Лучи AQ и AO — биссектрисы смежных углов, так как касательные к окружностям равноудалены от центра. Так как AQ и AO — биссектрисы смежных углов, то угол OAQ прямой — смежные углы в сумме дают 180°, значит сумма их биссектрис:

Далее рассмотрим прямоугольный треугольник OAQ. По свойству высоты в прямоугольном треугольнике, получаем:

📸 Видео

Построение касательной к окружности.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Касательная к описанной окружности треугольника (Задача №324602)Скачать

8 класс, 32 урок, Касательная к окружностиСкачать

Задание 26 Свойство касательной и секущей Подобные треугольникиСкачать

Равнозвенная ломаная и касательная к описанной окружности | Готовимся ко ВсероссуСкачать

#59. Олимпиадная задача о касательной к окружности!Скачать

ЕГЭ по математике. Задание №16 #11Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ в точке ЗАДАЧИ 8 классСкачать

Строим касательную к окружности (Задача 3).Скачать

#4 Самое сложное задание 16 ОГЭ 2021. Углы в окружности. Касательная к окружности.Скачать

Касательная к окружности и её свойстваСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать