Касательная к окружности задачи 7 класс мерзляк самостоятельная

Геометрия 7 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 7 классе «Окружность и круг. Геометрические построения» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Ответов нет.

Геометрия 7 класс (УМК Мерзляк)
Контрольная работа № 4

Окружность и круг. Геометрические построения

Вариант 1

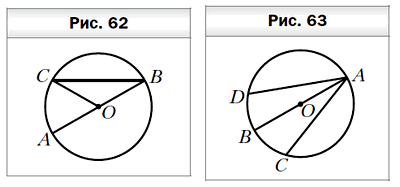
1. На рисунке 62 точка O — центр окружности, ∠ABC = 28°. Найдите угол AOC.
2. К окружности с центром O проведена касательная CD (D — точка касания). Найдите отрезок OC, если радиус окружности равен 6 см и ∠DCO = 30°.
3. В окружности с центром O проведены диаметр AB и хорды AC и AD так, что ∠BAC = ∠BAD (рис. 63). Докажите, что AC = AD. Постройте равнобедренный треугольник по боковой стороне и медиане, проведённой к ней.
4. Даны окружность и две точки вне её. Найдите на окружности точку, равноудалённую от этих двух точек. Сколько решений может иметь задача?

Вариант 2

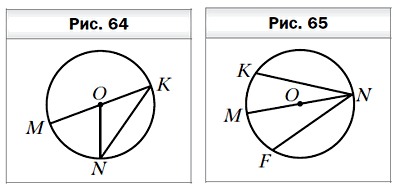
1. На рисунке 64 точка O — центр окружности, ∠MON = 68°. Найдите угол MKN.
2. К окружности с центром O проведена касательная AB (A — точка касания). Найдите радиус окружности, если OB = 10 см и ∠ABO = 30°.
3. В окружности с центром O проведены диаметр MN и хорды NF и NK так, что NF = NK (рис. 65). Докажите, что ∠MNK = ∠MNF.
4. Постройте треугольник по двум сторонам и медиане, проведённой к одной из них.
5. Даны прямая и две точки вне её. Найдите на этой прямой точку, равноудалённую от этих двух точек. Сколько решений может иметь задача?

Вариант 3

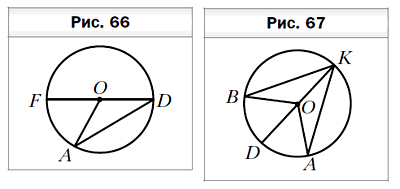
1. На рисунке 66 точка O — центр окружности, ∠OAD = 34°. Найдите угол FOA.
2. К окружности с центром O проведена касательная MN (M — точка касания). Найдите отрезок MN, если ON = 12 см и ∠NOM = 30°.
3. В окружности с центром O проведены диаметр DK и хорды KA и KB так, что ∠OAK = ∠OBK (рис. 67). Докажите, что AK = BK.
4. Постройте равнобедренный треугольник по основанию и медиане, проведённой к нему.
5. Даны угол и окружность. Найдите на окружности точку, принадлежащую углу и равноудалённую от его сторон. Сколько решений может иметь задача?

Вариант 4

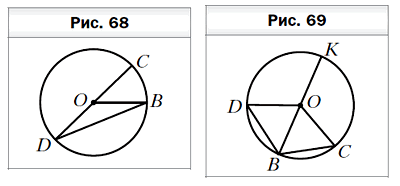
1. На рисунке 68 точка O — центр окружности, ∠BOC = 40°. Найдите угол OBD.
2. К окружности с центром O проведена касательная FK (K — точка касания). Найдите отрезок FK, если радиус окружности равен 14 см и ∠FOK = 45°.
3. В окружности с центром O проведены диаметр KB и хорды BC и BD так, что ∠BOC = ∠BOD (рис. 69). Докажите, что BC = BD.
4. Постройте равнобедренный треугольник по боковой стороне и высоте, проведённой к ней.
5. Даны угол и две точки. Найдите точку, принадлежащую углу, равноудалённую от его сторон и равноудалённую от двух данных точек. Сколько решений может иметь задача?

Вы смотрели: Геометрия 7 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 7 классе «Окружность и круг. Геометрические построения» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Цитаты из пособия «Геометрия 7 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Видео:НЕКОТОРЫЕ СВОЙСТВА ОКРУЖНОСТИ. КАСАТЕЛЬНАЯ к окружности. §20 геометрия 7 классСкачать

Геометрия 7 Контрольная 4 (Мерзляк): 2 комментария

Ит ис реал вариант, который будет на кр?))))

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Предметы

Видео:МЕРЗЛЯК-7 ГЕОМЕТРИЯ. СВОЙСТВА ОКРУЖНОСТИ. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ. ПАРАГРАФ-20Скачать

Новые работы

Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Найти контрольную:

Видео:МЕРЗЛЯК-7. ПАРАГРАФ-3. САМОСТОЯТЕЛЬНАЯ РАБОТА. ВАРИАНТ-1Скачать

Авторы работ и УМК

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Предметы

Видео:МЕРЗЛЯК-7. ГЕОМЕТРИЯ ПАРАГРАФ-4. САМОСТОЯТЕЛЬНАЯ РАБОТАСкачать

Важные страницы

Соглашение о конфиденциальности

(с) 2021. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru

Видео:Некоторые свойства окружности касательная к окружности - 7 класс геометрияСкачать

Популярное

Видео:7 класс. Касательная к окружностиСкачать

Предупреждение

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Видео:Касательная к окружности. Геометрия 7 классСкачать

Самостоятельная работа по геометрии «Некоторые свойства окружности. Касательная к окружности» 7 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:7 класс "Касательная к окружности"Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Некоторые свойства окружности. Касательная к окружности.
Вариант I.

№ 1. К окружности с центром О проведена касательная CD (D- точка касания). Найдите отрезок ОС, если радиус окружности равен 6 см и ∠ DCO=30°.

№ 2. На рис 1 прямая ВС касается окружности с центром О в точке В. Найдите ∠АОВ, если ∠АВС = 63°.

№ 3. На рис 2 прямые АС и АВ касаются окружности с центром О в точках С и В соответственно. Найдите ∠АСВ, если ∠ВАС = 72°.

Некоторые свойства окружности. Касательная к окружности.
Вариант II .

№ 1. К окружности с центром О проведена касательная AB (A- точка касания). Найдите
радиус окружности, если ОВ=10 см и ∠ АВO=30°.

№ 2. На рис 1 прямая АС касается окружности с центром О в точке А. Найдите ∠ВАС,
если ∠АОВ=108°.

№ 3. На рис 2 прямые АС и АВ касаются окружности с центром О в точках С и В соответственно. Найдите ∠ВАС, если ∠СОВ = 122°.

Некоторые свойства окружности. Касательная к окружности.
Вариант I .

№ 1. К окружности с центром О проведена касательная CD (D- точка касания). Найдите отрезок ОС, если радиус окружности равен 6 см и ∠ DCO=30°.

№ 2. На рис 1 прямая ВС касается окружности с центром О в точке В. Найдите ∠АОВ, если ∠АВС = 63°.

№ 3. На рис 2 прямые АС и АВ касаются окружности с центром О в точках С и В соответственно. Найдите ∠АСВ, если ∠ВАС = 72°.

Некоторые свойства окружности. Касательная к окружности.
Вариант II .

№ 1. К окружности с центром О проведена касательная AB (A- точка касания). Найдите
радиус окружности, если ОВ=10 см и ∠ АВO=30°.

№ 2. На рис 1 прямая АС касается окружности с центром О в точке А. Найдите ∠ВАС,
если ∠АОВ=108°.

№ 3. На рис 2 прямые АС и АВ касаются окружности с центром О в точках С и В соответственно. Найдите ∠ВАС, если ∠СОВ = 122°.

Некоторые свойства окружности. Касательная к окружности.
Вариант II .

№ 1. К окружности с центром О проведена касательная AB (A- точка касания). Найдите
радиус окружности, если ОВ=10 см и ∠ АВO=30°.

№ 2. На рис 1 прямая АС касается окружности с центром О в точке А. Найдите ∠ВАС,
если ∠АОВ=108°.

№ 3. На рис 2 прямые АС и АВ касаются окружности с центром О в точках С и В соответственно. Найдите ∠ВАС, если ∠СОВ = 122°.

Некоторые свойства окружности. Касательная к окружности.
Вариант I .

№ 1. К окружности с центром О проведена касательная CD (D- точка касания). Найдите отрезок ОС, если радиус окружности равен 6 см и ∠ DCO=30°.

№ 2. На рис 1 прямая ВС касается окружности с центром О в точке В. Найдите ∠АОВ, если ∠АВС = 63°.

№ 3. На рис 2 прямые АС и АВ касаются окружности с центром О в точках С и В соответственно. Найдите ∠АСВ, если ∠ВАС = 72°.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:МЕРЗЛЯК-7. САМОСТОЯТЕЛЬНАЯ РАБОТА, ПАРАГРАФ-1Скачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 513 053 материала в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 20. Некоторые свойства окружности. Касательная к окружности

Другие материалы

• 17.06.2019
• 361
• 17

• 14.06.2019
• 629
• 6

• 11.06.2019
• 1371
• 0

• 11.06.2019
• 1962
• 365

• 11.06.2019
• 681
• 2

• 09.06.2019
• 220
• 0

• 01.06.2019
• 244
• 3

• 01.06.2019
• 235
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 20.06.2019 5141
• DOCX 463.4 кбайт
• 415 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Кутузова Елена Игоревна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет
• Подписчики: 1
• Всего просмотров: 21959
• Всего материалов: 11

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Окружность. 7 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Большинство российских вузов используют смешанный формат обучения

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

Все школы Оренбурга переводят на дистанционное обучение с 28 января

Время чтения: 1 минута

В Новосибирской области школьников переведут на удаленку

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Урок «Некоторые свойства окружности. Касательная к окружности»
презентация к уроку по геометрии (7 класс)

Презентация к уроку геометрии для 7 класса, УМК Мерзляк А.Г.

Видео:Геометрия. 7 класс. Касательная к окружности /20.04.2021/Скачать

Скачать:

Предварительный просмотр:

Видео:Касательная к окружности | Геометрия 7-9 класс #69 | ИнфоурокСкачать

Подписи к слайдам:

Некоторые свойства окружности. Касательная к окружности

Повторение Окружность ( O;R ) AB – диаметр ОС = ОА = ОВ – радиусы АС — хорда А B O C

Теорема 20.1 Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам. Дано: Окр .( O; R) АВ – хорда CD – диаметр CD АВ Доказать: CD делит АВ пополам. Доказательство: 1 случай Если хорда АВ – диаметр, то CD пересекает АВ в точке О, значит, АО = ВО. А O C D В

Теорема 20.1 Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам. Дано: Окр .( O; R) АВ – хорда CD – диаметр CD АВ Доказать: CD делит АВ пополам. Доказательство: 2 случай Если хорда АВ – не диаметр, то CD пересекает АВ в точке М. Докажем, что АМ = МВ. Д. п. Проведем радиусы ОА и ОВ . Рассмотрим треугольник АОВ – равнобедренный ( ОА = ОВ ). ОМ – высота и медиана (по свойству р/б треугольника), значит, АМ = МВ. А O C D В М

Теорема 20.2 Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде. А O C D М В

Рассмотрим взаимное расположение прямой и окружности. Вспомним , что называется расстоянием от точки до прямой? Расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки к этой прямой. СН а C а H

Рассмотрим взаимное расположение прямой и окружности. Обозначим ОН – расстояние от центра окружности О до некоторой прямой а . O r Если ОН > r , то прямая а и окружность не имеют общих точек. Н r Если ОН Мне нравится

📸 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ. СВОЙСТВО КАСАТЕЛЬНОЙ. Видеоурок | ГЕОМЕТРИЯ 7 классСкачать