Калькулятор вписанной и описанной окружности

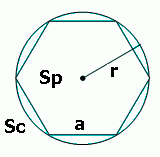
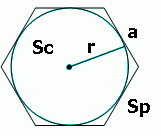
Расчет параметров вписанной в правильный многоугольник и описанной вокруг него окружности.

На самом деле у меня уже были сделаны калькуляторы для правильных многоугольников — Длина стороны правильного многоугольника. Один из первых запросов пользователей, между прочим. Эти калькуляторы находили параметры правильного многоугольника, исходя из величины радиуса описанной или вписанной в него окружности.

Калькуляторы ниже решают обратную задачу — исходя из параметров многоугольника, находят параметры вписанной и описанной окружностей.
Радиус вписанной окружности (incircle):

Площадь правильного многоугольника:

Радиус описанной окружности (circumcircle):

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Радиус вписанной и описанной окружности

В немногие из многоугольников можно вписать окружность. Окружность будет называться вписанной в многоугольник, если она касается всех его сторон. При этом, поскольку каждая сторона является касательной к окружности, то из свойств последней следует, что она находится под прямым углом к радиусу вписанной окружности. Радиусы, проведенные к сторонам многоугольника из центра окружности, имеют первостепенное значение, так как они фигурируют во многих расчетах по данным фигурам, в том числе и без окружности, как таковой. Центр окружности, вписанной в многоугольник, можно найти, проведя две биссектрисы из любых углов, точка их пересечения и будет искомым центром. Для того чтобы различать в формулах радиусы вписанной и описанной окружностей их обозначают r и R соответственно длине.

Вокруг определенных геометрических фигур можно описать окружность. Если для каждой стороны провести срединный перпендикуляр, или медиатрису, то точка их пересечений (достаточно двух) будет центром описанной вокруг фигуры окружности. Такая окружность содержит все вершины углов многоугольника. Радиусы, соединяющие центр окружности с вершинами многоугольника, участвуют во многих вычислениях и решениях типовых задач на нахождение сторон, площадей и других параметров данных фигур. Радиусы описанных окружностей обозначаются R , а радиусы вписанных окружностей – r , для различия.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Окружность и круг. Онлайн калькулятор

С помощю этого онлайн калькулятора окружности можно найти радиус, диаметр, площадь окружности и т.д. по известным элементам. Для нахождения элементов окружности выберите требуемый элемент для вычисления, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

1. Определение окружности

Определение 1. Окружность − это геометрическая фигура состоящая из всех точек плоскости равноудаленных от данной точки O (Рис.1).

Точка O называется центром окружности. Отрезок, соединяющий центр окружности с какой-либо точкой окружности, называется радиусом окружности. Длина этого отрезка также называют радиусом окружности. Из определения 1 следует, что все радиусы окружности имеют одну и ту же длину.

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

2. Хорда

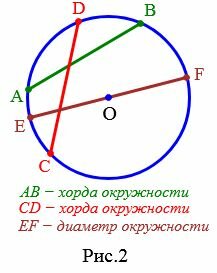
Отрезок, соединяющий две точки окружности, называется хордой (Рис.2). Хорда, проходящая через центр окружности, называется диаметром.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

3. Дуга окружности

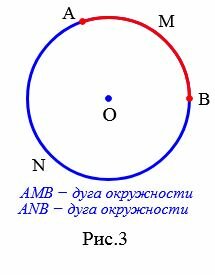
Отметим на окружности любые две точки A и B. Эти точки делят окружность на две части. Каждая из которых называется дугой окружности (Рис.3). Чтобы различать эти дуги, на каждой из них отмечают промежуточную точку. Например M и N (Рис.3). Обозначают эти дуги так: ◡AMB и ◡ANB. Иногда в обозначении промежуточную точку пропускают, если известно о какой дуге идет речь.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

4. Полуокружность

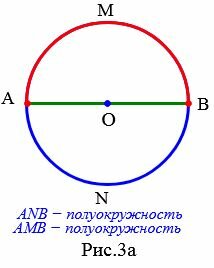
Дуга называется полуокружностью, если отрезок, соединяющий ее концы является диаметром окружности. На рисунке 3a изображены две полуокружности: AMB и ANB.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

5. Определение круга

Определение 2. Круг − это геометрическая фигура состоящая из всех точек плоскости удаленных от данной точки O на рассояние не больше заданного неотрицательного числа R (Рис.4).

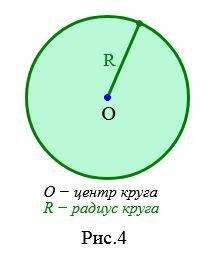O − называется центром круга. R− радиус круга. Из определения 2 следует, что окружность является частью круга. Такой круг называется замкнутым.

Представим другое определение круга.

Определение 3. Круг − это геометрическая фигура состоящая из всех точек плоскости удаленных от данной точки O на рассояние меньше заданного неотрицательного числа R (Рис.5).

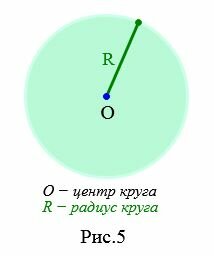В этом определении окружность не входит в круг. Такой круг называется открытым.

Еще одно определение круга.

Определение 4. Круг − это часть плоскости, которая лежит внутри окружности.

Обычно под понятием круг понимают замкнутый круг. Если имеется в виду открытый круг, то надо об этом объявить.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

6. Сектор круга

Определение 5. Часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга называется сектором круга.

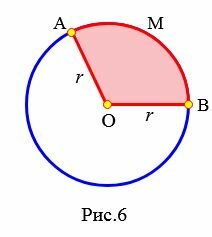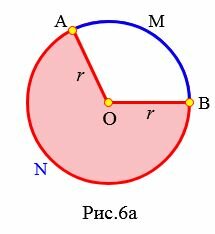На рисунке 6 окрашенная поверхность − это сектор окружности с центром O. Он находится между дугой AMB и двумя радиусами OA и OB. На рисунке 6a окрашенная поверхность − это сектор окружности с центром O. Он находится между дугой ANB и двумя радиусами OA и OB.

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

7. Сегмент круга

Определение 6. Часть круга, ограниченная дугой и ее хордой называется сегментом круга.

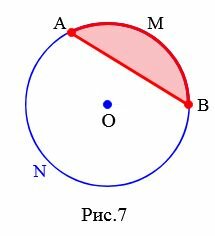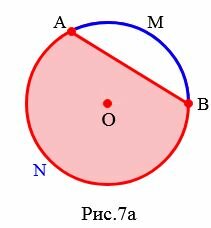На рисунке 7 окрашенная поверхность − это сегмент окружности с центром O. Он находится между дугой AMB и ее хордой AB. На рисунке 7a окрашенная поверхность − это сегмент окружности с центром O. Он находится между дугой ANB и ее хордой AB.

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

8. Полукруг

Определение 7. Сегмент круга, хордой которого является диаметр этого круга называется полукругом.

На рисунке 8 окрашенная поверхность − это полукруг. Он находится между дугой AMB и ее хордой AB, которая является диаметром данной окружности.

🔥 Видео

Вписанная и описанная окружности. ЗадачиСкачать

Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

8 класс, 39 урок, Описанная окружностьСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Какие калькуляторы можно использовать на ЕГЭ по физике?Скачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать