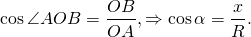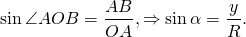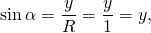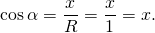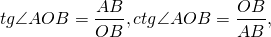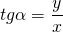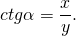Какую точку единичной окружности называют точкой соответствующей углу альфа (2 видео)

Информационные технологии на уроках математики

Разделы: Математика

Тема урока: Определение синуса и косинуса угла.

Цели урока:

ввести определение синуса и косинуса любого угла; отработать алгоритм нахождения синуса и косинуса на числовой окружности;
развивать логическое мышление, умение обобщать.
воспитывать самостоятельность, ответственность, творческое отношение к деятельности.

Тип урока: объяснения нового материала сопровождается показом презентации. (Приложение 1)

Формы работы: фронтальный опрос, фронтальное обсуждение и решение у доски.

Оборудование: компьютер, проектор, экран, шарнирная модель с изображением на миллиметровой бумаге окружности большого радиуса, на которой нанесены градусные меры с шагом в 30 градусов, и с подвижным радиусом, чертежные инструменты.

1. Приветствие

Сообщение темы и целей урока.

2. Введение в атмосферу урока

Показ учебной презентации с помощью видеопроектора. (Слайд 1)
Запишите тему урока: «Определение синуса и косинуса угла». Как называется раздел математики, зашифрованный в ребусе. (Слайд 2)
Ответ: Тригонометрия.
Слово “тригонометрия” (от греческих слов “тригонон” – треугольник и “метрео” – измеряю) означает “измерение треугольников”. Возникновение тригонометрии связано с развитием астрономии – науки о движении небесных тел, о строении и развитии Вселенной. (Слайд 3)

3.Фронтальный опрос

Вы уже знакомы с понятием синус и косинус и можете найти синус и косинус углов, радианная мера которых заключена между 0 и . (Слайд 4). Найдите cos150 о ; sin45 о ; sin0 о ; sin30 о ; sin120 о ; cos135 о ; cos90 о ; cos60 о .

4. Объяснение нового материала

А как найти значение sin240 о и cos240 о ? Как определить синус и косинус любого угла? (Слайд 5)
Для этого рассмотрим прямоугольную систему координат и окружность единичного радиуса с центром в начале координат. Пусть подвижный вектор, совершив поворот от вектора ОА до вектора ОВ, образовал угол АОВ, радианная мера которого равна радиан. Точку В назовем точкой, соответствующей углу , или коротко, точкой . Заметим, что если точка В соответствует числу , то она соответствует и всем числам вида + 2к, где к – целое число. Положение точки В будет определяться углом поворота с одной стороны, с другой стороны координатами (X; Y) в прямоугольной системе координат. (Слайд 6)
Какая связь между координатами (X; Y) и углом поворота А?

Учащиеся делают вывод: X = cos А; Y = sin ?. (Слайд 7)

Определение: Число, равное ординате точки единичной окружности, соответствующей углу , называют синусом угла . Число, равное абсциссе точки единичной окружности, соответствующей углу , называют косинусом угла . (Слайд 8)

Из сказанного выше следует, что для любого угла существует и притом единственный синус и косинус, значит синус и косинус являются функциями угла.

Пример 1: Найдем значение sin240 о и cos 240 о . Для этого:

1. На числовой окружности найдем точку, соответствующую углу поворота 240 о .
2. Найдем координаты этой точки.
3. X = cos240 о ; Y = sin240 о . (Слайды 9, 10)

5. Закрепление

Учащиеся на доске. № 7.31. Найдите cos0 о ; sin0 о ; cos270 о ; sin270 о .

Показать, как заполняется таблица значений тригонометрических функций аргументов от 0 до 2 о . Для этого рассмотреть прямоугольный треугольник с гипотенузой, равной 1. Для точки /4 все сводится к рассмотрению равнобедренного прямоугольного треугольника. Его катеты равны 2/2, 2/2; значит, координаты точки /4 (2/2, 2/2) Аналогично обстоит дело с точками 3/4, 5/ 4, 7/4, но разница лишь в знаках абсциссы и ординаты. Запомните, что модули абсциссы и ординаты у середин всех четвертей равны 2/2, а знаки определяются по чертежу. (Слайд 11). Для точки /6 все сводится к рассмотрению прямоугольного треугольника с гипотенузой 1 и углом 30 о . Тогда катет, противолежащий углу 30 о будет равен 1/2 , а прилежащий катет равен 3/2 . Значит, координаты точки /6 (3/2, 1/2) . Для точки /3 (1/2, 3/2). (Слайд 12)

6. Беседа по вопросам

1. Какую окружность в тригонометрии называют единичной окружностью?
Ответ: Единичной окружностью в тригонометрии называют окружность радиуса 1 с центром в начале координат.

2. Какую точку единичной окружности называют точкой, соответствующей углу ?
Ответ: точку В назовем точкой, соответствующей углу , если подвижный вектор, совершив поворот от вектора ОА до вектора ОВ, образовал угол АОВ, радианная мера которого равна радиан.

3. Какая связь между координатами (X; Y) и углом поворота ?
Ответ: Абсциссу х называют косинусом числа , а ординату y называют синусом числа .

4. Почему синус и косинус являются функциями угла?
Ответ: Синус и косинус являются функциями угла, потому что для любого угла существует и притом единственный синус и косинус.

5. Какие значения могут принимать синус и косинус?
Ответ: Синус и косинус принимают значения от –1 до 1.

6. Синус и косинус имеют одинаковые знаки, в какой четверти находится угол?
Ответ: Синус и косинус положительны в первой четверти и отрицательны в третьей четверти.

7. Подведение итогов, домашнее задание: П.7.3. № 7.33–7.35.

Содержание

Единичная окружность
One Comment
Алгебра
Числовая и единичная окружность
Откладывание углов на единичной окружности
🎦 Видео

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Единичная окружность

Что такое единичная окружность и как с ее помощью вводятся определения синуса, косинуса, тангенса и котангенса?

Рассмотрим в прямоугольной декартовой системе координат окружность с центром в начале координат — точке O.

Отметим на окружности точку P, лежащую на оси абсцисс справа от точки O.

Осуществим поворот радиуса OP около точки O на угол α в верхнюю полуплоскость.

При этом радиус OP займет положение OA. Говорят, что при повороте на угол альфа радиус OP переходит в радиус OA, а точка P переходит в точку точку A(x;y).

Опустив перпендикуляр AB из точки A на ось Оx, получим прямоугольный треугольник OAB, в котором гипотенуза OA равна радиусу окружности, катеты AB и OB — ординате и абсциссе точки A: OA=R, AB=y, OB=x.

Катет AB — противолежащий углу AOB, равному α, катет OB — прилежащий.

По определению косинуса острого угла в прямоугольном треугольнике,

Таким образом, на окружности косинус угла α — это отношение абсциссы точки A окружности к радиусу этой окружности.

Аналогично, по определению синуса острого угла в прямоугольном треугольнике,

Значит, синус угла α — это отношение ординаты точки A окружности к радиусу этой окружности.

Для окружности любого радиуса отношения x/R и y/R не зависят от величины радиуса, а зависят только от угла альфа. Поэтому удобно взять R=1. Для окружности единичного радиуса определение синуса и косинуса упрощаются:

Окружность с центром в начале координат и радиусом, равным единице, называется единичной окружностью.

Отсюда получаем определения синуса и косинуса на единичной окружности.

Синусом угла α называется ордината точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Косинусом угла α называется абсцисса точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Применив определения тангенса и котангенса острого угла в прямоугольном треугольнике в ∆AOB, получаем:

Приходим к определению тангенса и котангенса на единичной окружности.

Тангенсом угла α называется отношение ординаты точки A единичной окружности к абсциссе этой точки.

Котангенсом угла α называется отношение абсциссы точки A единичной окружности к ординате этой точки.

Видео:Как искать точки на тригонометрической окружности.Скачать

One Comment

Искала везде. Нигде нет такого подробного и понятного объяснения. Огромное Вам спасибо!

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Алгебра

План урока:

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Числовая и единичная окружность

В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.

Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.

Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:

Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.

Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.

Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:

В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.

Выглядит единичная окружность так:

Видео:Тригонометрическая окружность. Как выучить?Скачать

Откладывание углов на единичной окружности

Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:

Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.

Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:

Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:

Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:

В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.

Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:

Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:

Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:

Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.

Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:

С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:

Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:

Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:

Например, верны следующие равенства:

15° + 3•360° = 15° + 1080° = 1095°

100° + 10•360° = 100° + 3600° = 3700°

1000° = 1000° – 2•360° = 1000° – 720° = 280°

Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5