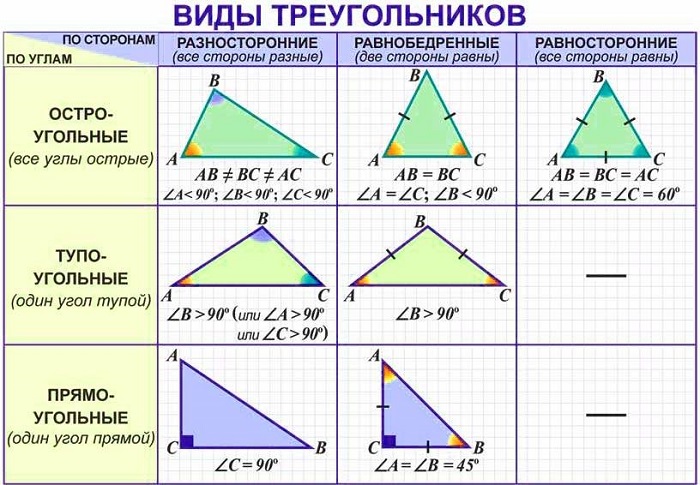
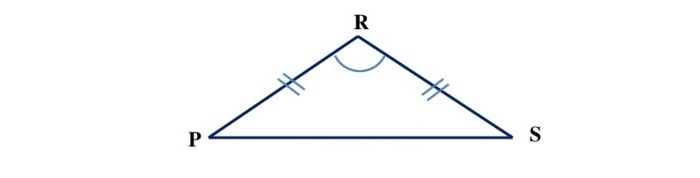
Какой треугольник называется остроугольным чертеж (7 видео)

Виды треугольников

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.

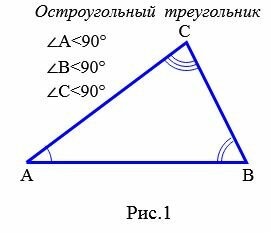
Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).

Какой треугольник называется остроугольным чертеж

Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).

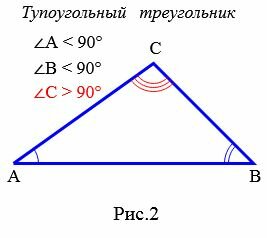Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).

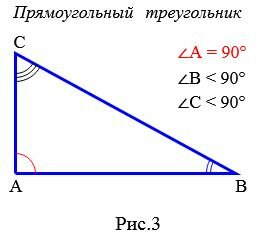Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

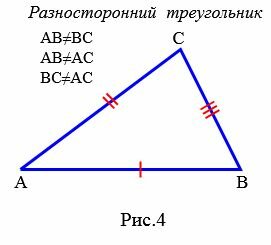
Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).

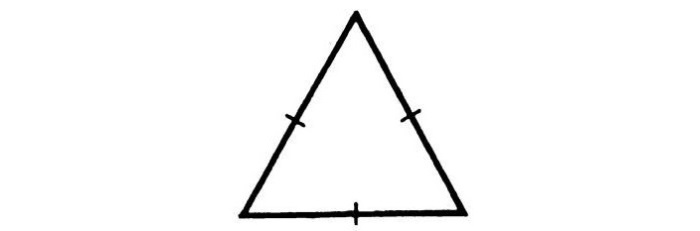
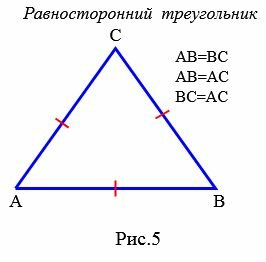
Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).

Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).

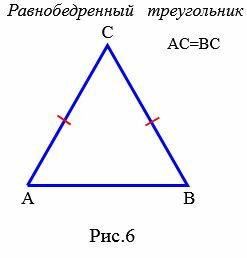В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.

Содержание

Остроугольный треугольник — виды, свойства и признаки
Виды, признаки и свойства остроугольных треугольников
Равносторонний треугольник
Разносторонний треугольник
Равнобедренный остроугольный треугольник
Равнобедренный тупоугольный треугольник
Виды треугольников (по сторонам)
💡 Видео

Видео:Виды треугольниковСкачать

Остроугольный треугольник — виды, свойства и признаки

Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.

Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Виды, признаки и свойства остроугольных треугольников

Трехсторонние фигуры разделяются на множество подвидов и категорий.

Общая классификация по наибольшему углу делит их на 3 группы:

Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.

3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;

сумма длин любых двух сторон больше оставшейся третьей.

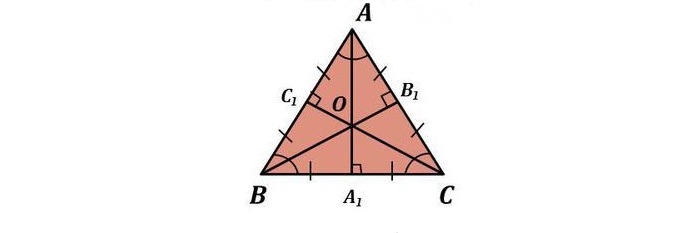
Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:

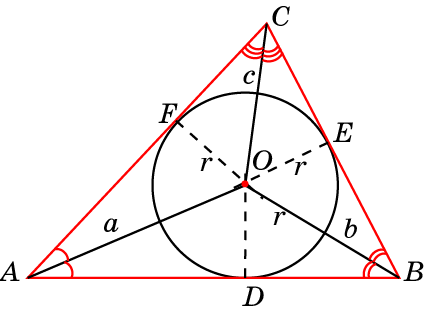
1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.

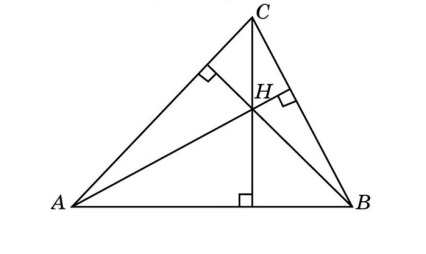
2. Высоты пересекаются в одной точке, образуя ортоцентр.

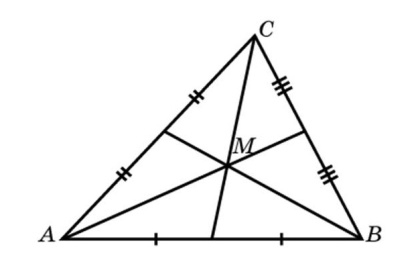
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).

Уникальные особенности зависят от разновидностей фигуры.

Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Равносторонний треугольник

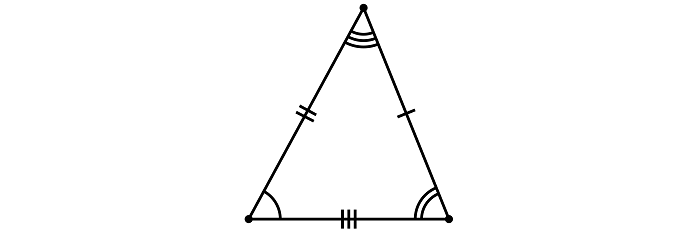
«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.

Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.

Видео:ТреугольникСкачать

Разносторонний треугольник

Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.

Уникальных отличий не имеет, только общие:

все параметры имеют разные значения;

совпадений между вспомогательными линиями нет.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Равнобедренный остроугольный треугольник

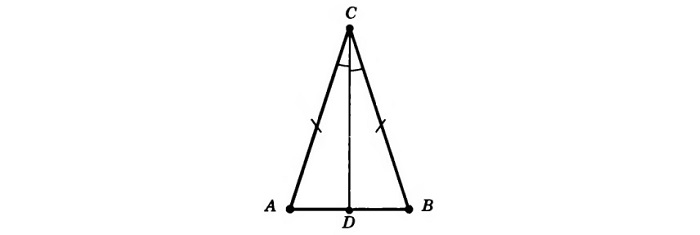
Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.

проведенная к основанию линия – и биссектриса, и высота, и медиана;

вспомогательные линии из крайних точек при основании совпадают.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Равнобедренный тупоугольный треугольник

Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.

Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.

Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.

В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.

Видео:Виды треугольников: остроугольный, прямоугольный ,тупоугольный. Как начертить треугольникСкачать

Виды треугольников (по сторонам)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке учащимся предоставляется возможность обобщить знания о названиях и изученных свойствах геометрических фигур, познакомиться с основными свойствами треугольника, узнать виды треугольников по величине угла, по числу равных сторон, потренироваться в распознавании названных видов.