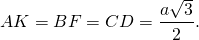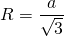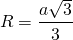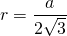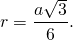В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Видео:№224. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60°Скачать
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Видео:как найти диагональ.Скачать
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Видео:Как найти диагональ... Диагональни топишСкачать

Свойства равностороннего треугольника
Основные свойства равностороннего треугольника непосредственно следуют из свойств равнобедренного треугольника, частным случаем которого он является.
Свойства равностороннего треугольника

AK — высота, медиана и биссектриса, проведённые к стороне BC;
BF — высота, медиана и биссектриса, проведённые к стороне AC;
CD — высота, медиана и биссектриса, проведённые к стороне AB.
Длины всех трёх высот (медиан, биссектрис) равны между собой:
Если a — сторона треугольника, то
3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:
5) Расстояние от точки пересечения высот, биссектрис и медиан
до любой вершины треугольника равно радиусу описанной окружности:
6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности:
7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.
8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности:
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Правильный треугольник. Площадь правильного треугольника
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Пусть сторона правильного треугольника равна .
Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Задача решается в одну строчку. Радиус вписанной окружности .
. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной вокруг правильного треугольника, равен .
📽️ Видео
Диагонали в многоугольниках. Есть ли зависимость между количеством вершин и диагоналей в n-угольникеСкачать

Диагонали правильных многоугольниковСкачать

Диагонали многоугольникаСкачать

Все о правильном шестиугольнике за 1 минуту! #егэ2023 #математикапрофиль2023 #школаСкачать
Геометрия - Построение правильного треугольникаСкачать

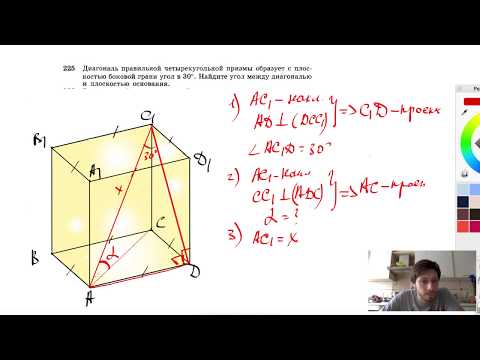
№225. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30°.Скачать
Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Задача о вычислении диагонали четырёхугольной призмыСкачать

Если в параллелограмме диагонали являются биссектрисами его угловСкачать

ЕГЭ Задание 8 Правильная шестиугольная призмаСкачать

Формулы равностороннего треугольника #shortsСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

8 класс, 2 урок, Выпуклый многоугольникСкачать

егэ векторы решу егэ все задания №2 профильСкачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать