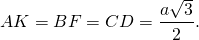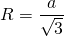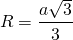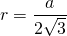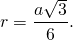В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Видео:Формулы равностороннего треугольника #shortsСкачать
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Видео:№576. Высота прямоугольного треугольника, проведенная из вершины прямого угла, делитСкачать
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать
Свойства равностороннего треугольника
Основные свойства равностороннего треугольника непосредственно следуют из свойств равнобедренного треугольника, частным случаем которого он является.
Свойства равностороннего треугольника
2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:
AK — высота, медиана и биссектриса, проведённые к стороне BC;
BF — высота, медиана и биссектриса, проведённые к стороне AC;
CD — высота, медиана и биссектриса, проведённые к стороне AB.
Длины всех трёх высот (медиан, биссектрис) равны между собой:
Если a — сторона треугольника, то
3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:
5) Расстояние от точки пересечения высот, биссектрис и медиан
до любой вершины треугольника равно радиусу описанной окружности:
6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности:
7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.
8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности:
Видео:Площадь равностороннего треугольникаСкачать
Какие вершины равностороннего треугольника
Ключевые слова: треугольник, сторона, угол, окружность вписанная, описанная
 |
 |
