Какие треугольники являются симметричными

О чем эта статья:

Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

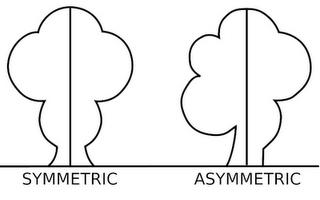
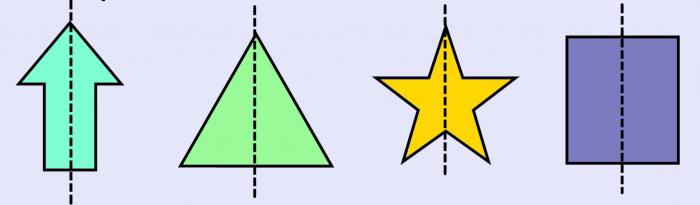
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

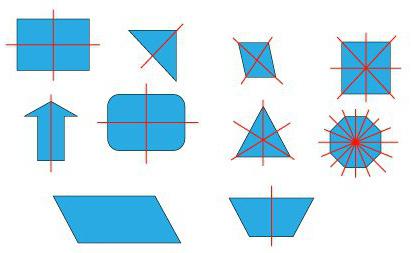
Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:Виды треугольниковСкачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Разбор фигуры Треугольник: технический анализ и правила торговлиСкачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Ось симметрииСкачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:Простая, но очень противная задача на окружности из ЕГЭ | Планиметрия 83 | mathus.ru #егэ2024Скачать

Что такое симметрия и асимметрия?

Симметрия ассоциируется с гармонией и порядком. И не зря. Потому что на вопрос, что такое симметрия, есть ответ в виде дословного перевода с древнегреческого. И получается, что она означает соразмерность и неизменность. А что может быть упорядоченней, чем строгое определение местоположения? И что можно назвать более гармоничным, чем то, что строго соответствует размерам?

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Что означает симметрия в разных науках?

Биология. В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии. Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.

Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.

Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.

Видео:Осевая симметрия. 6 класс.Скачать

Как определяют симметрию разные словари?

В какой бы из них мы ни заглянули, везде встретится слово «соразмерность». У Даля можно увидеть еще и такое толкование, как равномерие и равнообразие. Другими словами, симметричное — значит одинаковое. Здесь же говорится о том, что она скучна, интереснее смотрится то, в чем ее нет.

На вопрос, что такое симметрия, словарь Ожегова уже говорит об одинаковости в положении частей относительно точки, прямой или плоскости.

В словаре Ушакова упоминается еще и пропорциональность, а также полное соответствие двух частей целого друг другу.

Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Когда говорят об асимметрии?

Приставка «а» отрицает смысл основного существительного. Поэтому асимметрия означает то, что расположение элементов не поддается определенной закономерности. В ней отсутствует всякая неизменность.

В живой природе асимметрия играет важную роль. Причем она может быть как полезной, так и вредной. К примеру, сердце помещается в левую половину груди. За счет этого левое легкое существенно меньшего размера. Но это необходимо.

Видео:ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

О центральной и осевой симметрии

В математике выделяют такие ее виды:

• центральная, то есть выполненная относительно одной точки;
• осевая, которая наблюдается около прямой;
• зеркальная, она основывается на отражениях;
• симметрия переноса.

Что такое ось и центр симметрии? Это точка или прямая, относительно которой любой точке тела найдется другая. Причем такая, чтобы расстояние от исходной до получившейся делилось пополам осью или центром симметрии. Во время движения этих точек они описывают одинаковые траектории.

В ситуациях, когда необходимо найти центр симметрии, нужно поступать следующим образом. Если фигур две, то найти у них одинаковые точки и соединить их отрезком. Потом разделить пополам. Когда фигура одна, то помочь может знание ее свойств. Часто этот центр совпадает с точкой пересечения диагоналей или высот.

Видео:Треугольники: остро-, тупо- и прямоугольныеСкачать

Какие фигуры являются симметричными?

Геометрические фигуры могут обладать осевой или центральной симметрией. Но это не обязательное условие, существует множество объектов, которые не обладают ею вовсе. К примеру, параллелограмм обладает центральной, но у него нет осевой. А неравнобедренные трапеции и треугольники не имеют симметрии совсем.

Если рассматривается центральная симметрия, фигур, обладающих ею, оказывается довольно много. Это отрезок и круг, параллелограмм и все правильные многоугольники с числом сторон, которое делится на два.

Центром симметрии отрезка (также круга) является его центр, а у параллелограмма он совпадает с пересечением диагоналей. В то время как у правильных многоугольников эта точка тоже совпадает с центром фигуры.

Если в фигуре можно провести прямую, вдоль которой ее можно сложить, и две половинки совпадут, то она (прямая) будет являться осью симметрии. Интересно то, сколько осей симметрии имеют разные фигуры.

К примеру, острый или тупой угол имеет только одну ось, которой является его биссектриса.

Если нужно найти ось в равнобедренном треугольнике, то нужно провести высоту к его основанию. Линия и будет осью симметрии. И всего одной. А в равностороннем их будет сразу три. К тому же, треугольник обладает еще и центральной симметрией относительно точки пересечения высот.

У круга может быть бесконечное число осей симметрии. Любая прямая, которая проходит через его центр, может исполнить эту роль.

Прямоугольник и ромб обладают двумя осями симметрии. У первого они проходят через середины сторон, а у второго совпадают с диагоналями.

Квадрат же объединяет предыдущие две фигуры и имеет сразу 4 оси симметрии. Они у него такие же, как у ромба и прямоугольника.

Видео:ПАТТЕРН ТРЕУГОЛЬНИК В ТРЕЙДИНГЕ - ВСЯ СУТЬ!Скачать

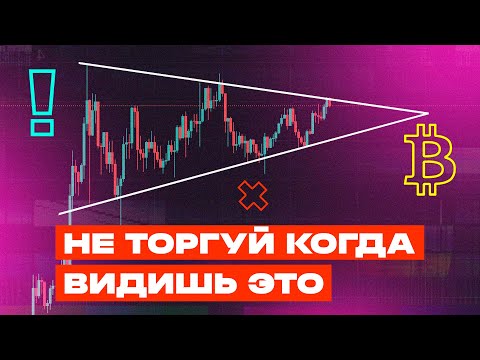
Технический анализ. Треугольники. Часть первая

Среди фигур технического анализа треугольники занимают почётное место. Есть несколько видов треугольников. Они достаточно часто встречаются на графиках и в основном служат признаками продолжения тенденции, но при определённых обстоятельствах указывают на разворот.

Фигуры продолжения обычно означают, что период коррекции является не более чем паузой в развитии основной тенденции и направление движения цен останется прежним после их завершения.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Симметричный треугольник

Этот тип треугольников образуется двумя сходящимися линиями, где верхняя линия опускается, а нижняя поднимается. В данном случае не стоит придавать слову «симметричный» такой же смысл, как в геометрии, то есть линии, образующие треугольник, не обязательно будут равны.

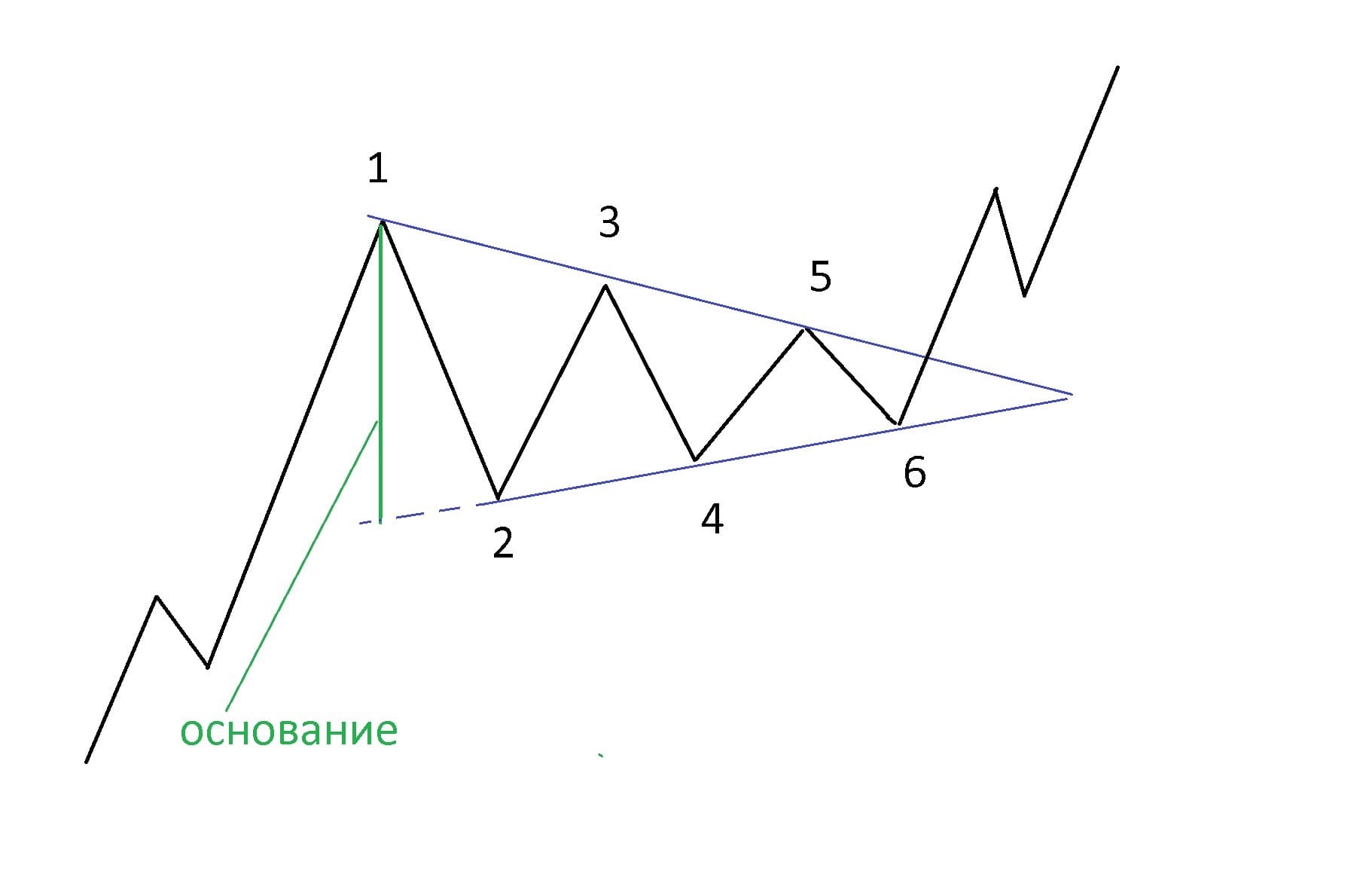
Минимальным требованием для построения любого треугольника является наличие четырёх точек — две сверху и две снизу. В действительности треугольники могут иметь шесть таких точек.

«Симметричный треугольник», как правило, является фигурой продолжения тенденции.

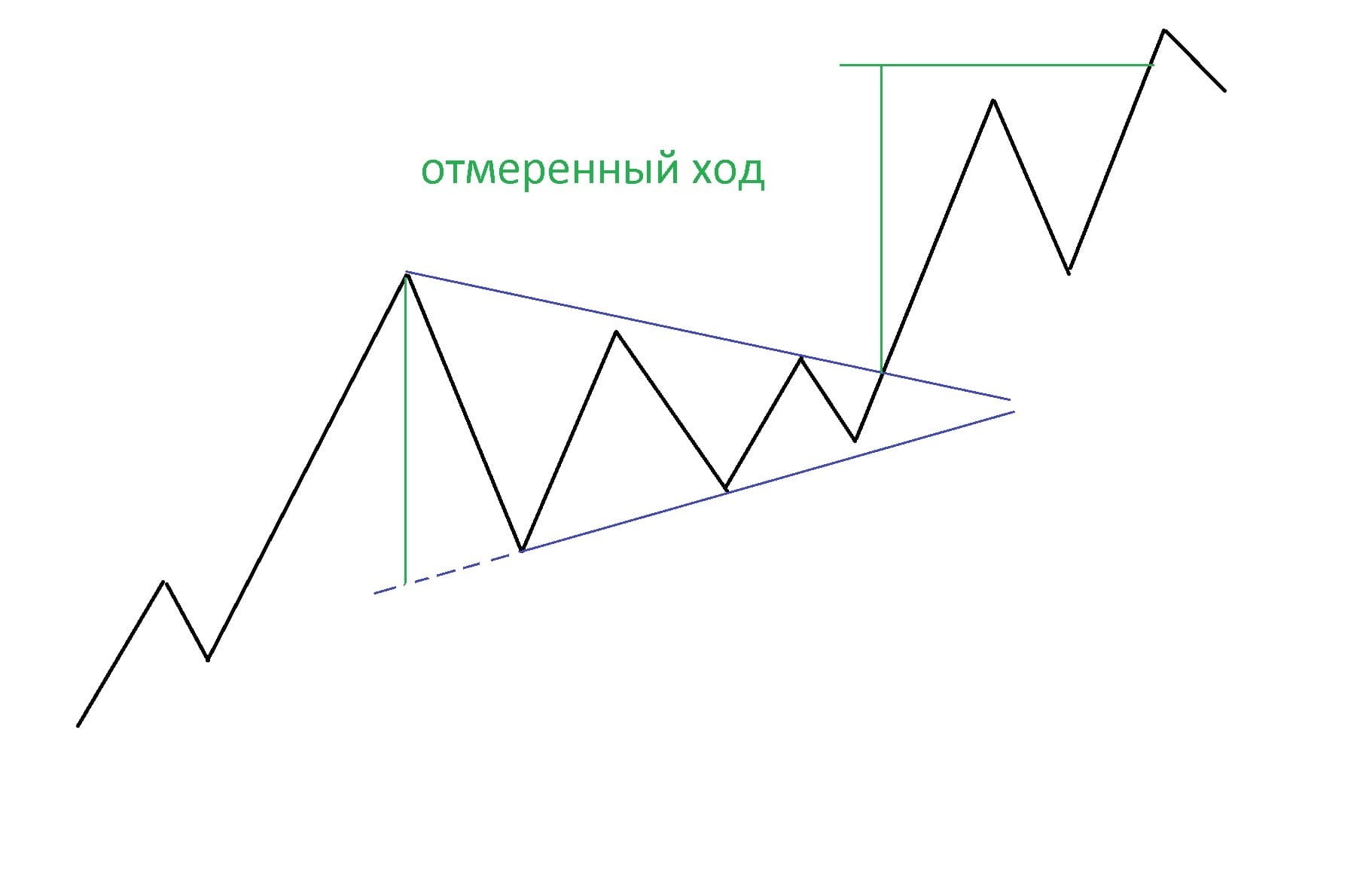
Высота, проведённая из точки 1 к продолжению нижней линии, называется основанием треугольника, а точка пересечения линий — это вершина. Фигура сохраняется до тех пор, пока цена не пробьёт одну из линий. При выходе нередко цена возвращается к пробитой линии, отбой от которой позволяет присоединиться к начавшемуся движению.

Выход цены из треугольника должен быть в пределах от 50% до 75% ширины треугольника по горизонтали.

Под шириной треугольника понимается расстояние от основания фигуры до её вершины.

Если цены не вышли из треугольника в этих пределах, фигура начинает терять свой потенциал.

Это означает, что цены продолжат движение к вершине треугольника, а затем — дальше, за её пределы. При этом боковая тенденция сохраняется и принимает иную форму, но опираться в анализе на эту фигуру уже не стоит.

Видео:Фигура тех анализа Симметричный треугольник | Обучение трейдингу #трейдингкриптовалютСкачать

Построение целевых ориентиров

Существует два способа определения цели для движения цены после пробоя. Один из них уже известен и состоит в измерении высоты основания, которая затем откладывается от точки пробоя.

Этот способ уже был описан ранее в статье про фигуру «Голова и плечи».

Другой способ позволяет построить цель, проводя параллельную линию из точки основания треугольника.

Этот способ аналогичен построению границ канала. Из вершины 1 проводится линия параллельно линии поддержки в треугольнике.

Оба способа построения цели равновесны, поэтому их можно использовать одновременно.

Не забываем о том, что построение цели на графиках — это лишь предположение и не обязывает цену поступать соответствующе.

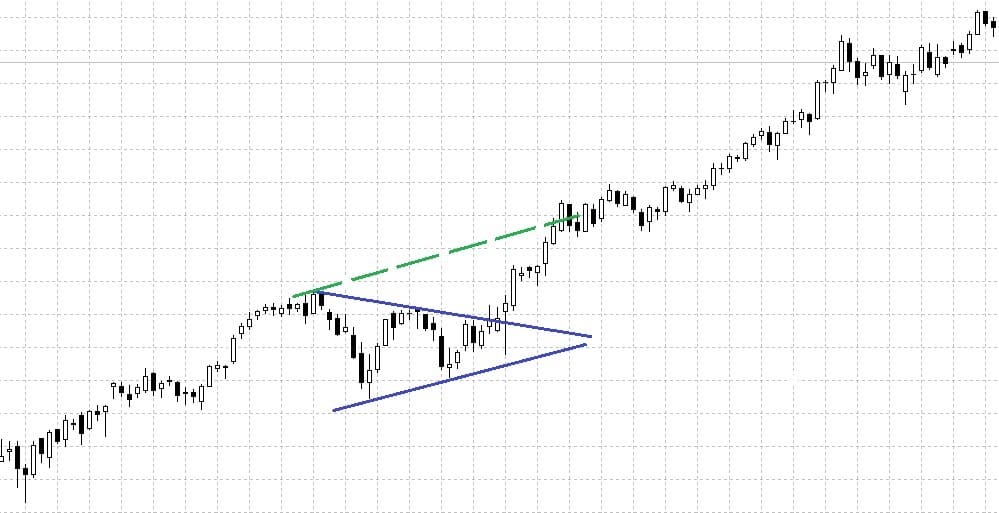
На восходящем движении образуется коррекция. Её форма соответствует фигуре «Симметричный треугольник», указывающей на продолжение роста. Ценовой ориентир получаем первым способом, измеряя высоту основания и откладывая её от точки пробоя.

В данном случае цель определена вторым способом. Из основания треугольника проведена линия параллельно нижней границе треугольника.

Симметричный треугольник на падающем рынке также выступает фигурой продолжения. Имеет аналогичные свойства и характеристики.

Видео:Осевая и центральная симметрия, 6 классСкачать

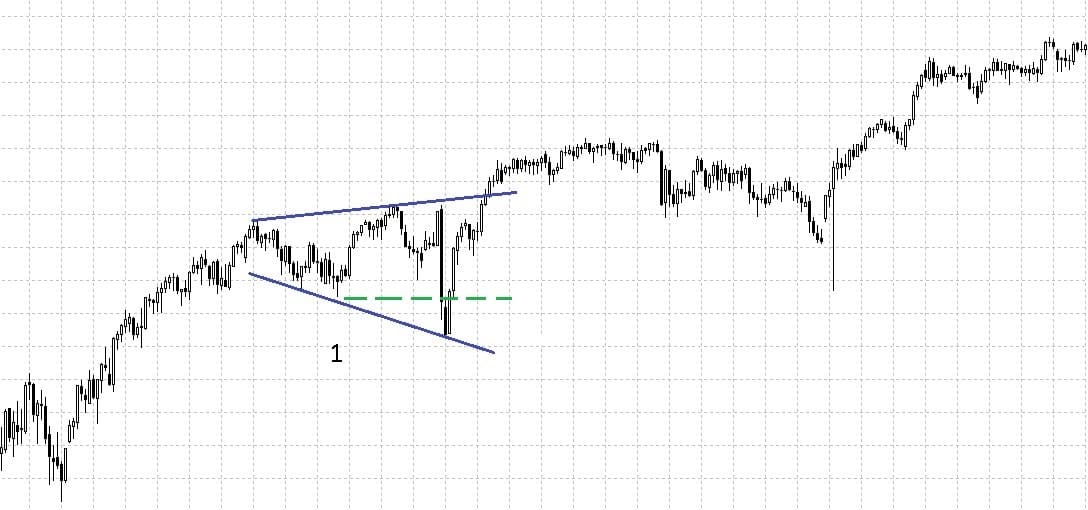
Расширяющийся треугольник

Этот вид треугольников отличается от симметричного тем, что начинается с вершины и движется к основанию, увеличивая размах колебания. Линии, ограничивающие его, как и у «Симметричного треугольника», расходятся в разные стороны.

Использование этих треугольников иное, нежели симметричных. Основная проблема этого вида коррекций именно в том, что размах колебания увеличивается. Новый максимум создаёт ложный сигнал на рост, а пробой уровня коррекции в точке 1 создаёт ложный ориентир на падение. Построить цель из фигуры проблематично.

Расширяющийся треугольник нередко становится фигурой разворота.

Спекулянты, торгующие с плечом, шутят, что расширяющийся треугольник — это пила, которая перепилит любой депозит.

В следующей статье мы рассмотрим другие виды треугольников.

Информация, представленная в статье, не является призывом или рекомендацией к действию. Принимая решение совершать торговые операции на финансовых рынках, вы в полной мере осознаёте и принимаете на себя все риски.

При подготовке данного цикла статей были использованы материалы из книг: Дж. Швагер «Технический анализ. Полный курс», Т. Р. Демарк «Технический анализ — новая наука», С. Нисон «Японские свечи», Г. Моррис «Японские свечи».

С теорией всё более-менее понятно, а что насчёт практики? Откройте брокерский счёт онлайн в «Открытие Брокер» и начинайте торговать прямо сейчас! А мы поможем советами и рекомендациями — всё самое полезное каждую неделю будет приходить прямо на ваш email, если подпишетесь на рассылку.

Без минимальной суммы, платы за обслуживание и скрытых комиссий

проект «Открытие Инвестиции»

Москва, ул. Летниковская, д. 2, стр. 4

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

🌟 Видео

Центральная симметрия. 6 класс.Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Сделка №7 Симметричный треугольник - "Курс молодого трейдера"Скачать

Технический анализ треугольник [Артём Звёздин]Скачать

Симметрия относительно точки (центральная симметрия). Пример 2Скачать

Виды треугольниковСкачать