Какие точки числовой окружности удовлетворяют неравенству x 2 1

Алгебра | 10 — 11 классы

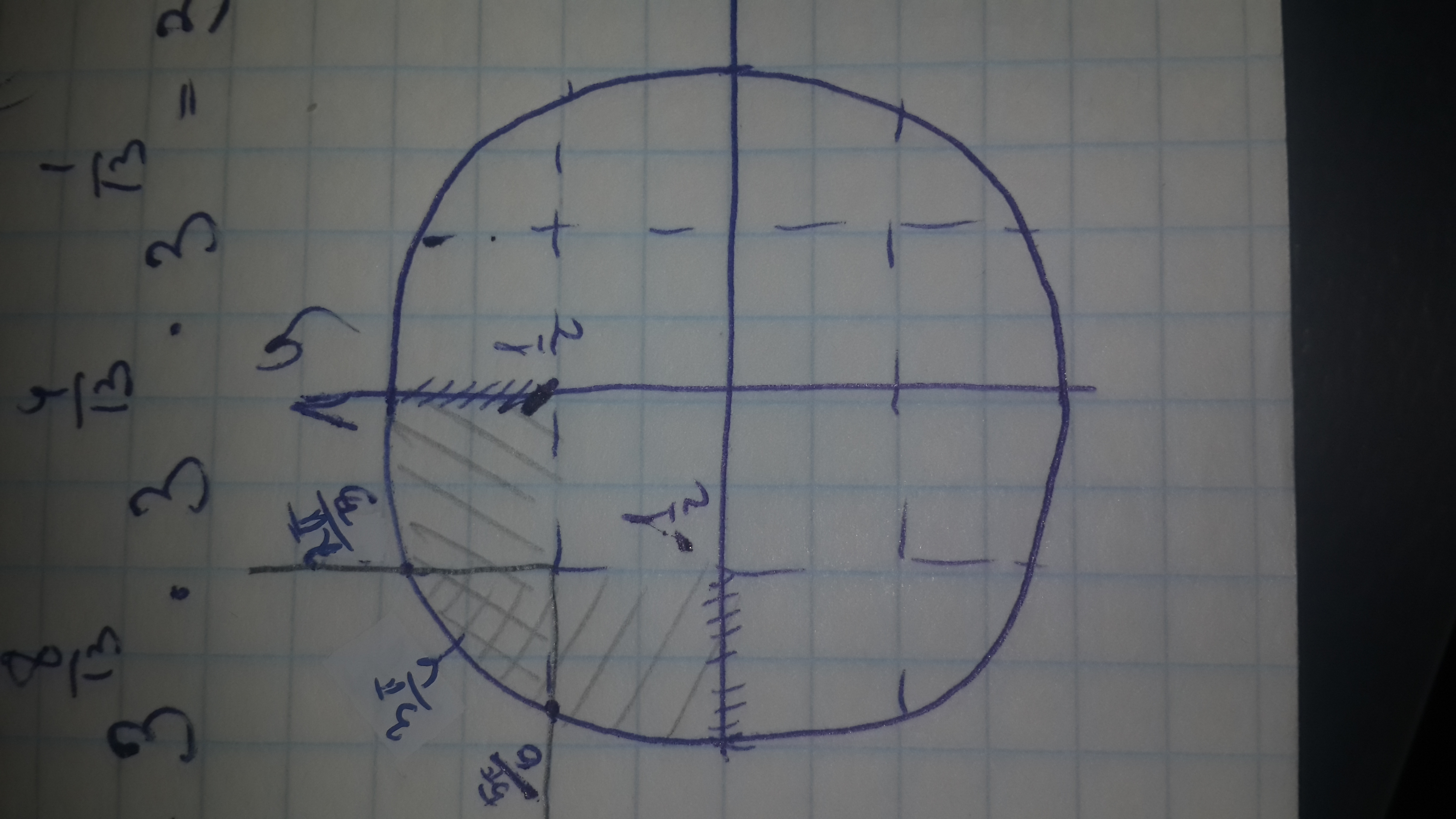
Найдите на числовой окружности все точки удовлетворяющие системе неравенств х&lt ; — 1 / 2 y&gt ; 1 / 2

запишите в виде двойного неравенства , каким числам t они соответствуют.

Видео:Как искать точки на тригонометрической окружности.Скачать

Между какими целыми числам располагается число (ответ запишите в виде двойного неравенства) √20 ; — √5?

Между какими целыми числам располагается число (ответ запишите в виде двойного неравенства) √20 ; — √5.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Между какими целыми числам располагается число (ответ запишите в виде двойного неравенства) √17 ; — √10?

Между какими целыми числам располагается число (ответ запишите в виде двойного неравенства) √17 ; — √10.

Видео:Точки на числовой окружностиСкачать

ПомогитееееНайдите наименьшее значение , удовлетворяющее системе неравенств?

Найдите наименьшее значение , удовлетворяющее системе неравенств.

Видео:Координаты точек на числовой окружности. Алгебра 10 класс.Скачать

Найдите наибольшее целое число, удовлетворяющее неравенству ?

Найдите наибольшее целое число, удовлетворяющее неравенству :

Видео:10 класс. Числовая окружность на координатной плоскости.Скачать

Найдите наибольшее значение икс, удовлетворяющие системе неравенств<5х + 12 = — 23?

Найдите наибольшее значение икс, удовлетворяющие системе неравенств

Видео:Отыскание решений уравнений и неравенств на числовой окружности (10 класс)Скачать

— 8≤5 — 13х≤8 найти наименьшее и наибольшее целое число удовлетворяющие двойному неравенству?

— 8≤5 — 13х≤8 найти наименьшее и наибольшее целое число удовлетворяющие двойному неравенству.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Найдите все целые числа удовлетворяющие двойному неравенству 2?

Найдите все целые числа удовлетворяющие двойному неравенству 2.

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Запишите в виде двойного неравенства х = 36, 6 + — 0?

Запишите в виде двойного неравенства х = 36, 6 + — 0.

Видео:Числовая окружностьСкачать

Запишите в виде двойного неравенства х = 36, 3 = + — 0, 1?

Запишите в виде двойного неравенства х = 36, 3 = + — 0, 1.

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Запишите в виде двойного неравенства х = 36, 3 = + — 0, 1?

Запишите в виде двойного неравенства х = 36, 3 = + — 0, 1.

На этой странице сайта вы найдете ответы на вопрос Найдите на числовой окружности все точки удовлетворяющие системе неравенств х&lt ; — 1 / 2 y&gt ; 1 / 2запишите в виде двойного неравенства , каким числам t они соответствуют?, относящийся к категории Алгебра. Сложность вопроса соответствует базовым знаниям учеников 10 — 11 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

1) В первой и второй четвертях т. К при x∈R y>, либо = 0 2)Во второй и четвертой четвертях, т. К если x>0, то y.

Видео:тригонометрические неравенства и их системыСкачать

Числовая окружность

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac, frac, frac, 10π, -frac)) разбирается в этой статье .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки — положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);

4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:

Длина числовой окружности равна (2π) или примерно (6,28).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.

Видео:Как решать тригонометрические неравенства?Скачать

Какие точки соответствуют числам (1), (2) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac),(-frac),(frac), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Видео:Числовая окружность на координатной плоскости | Алгебра 10 класс #10 | ИнфоурокСкачать

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .

В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .

Что надо запомнить про числовую окружность:

Видео:ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Решение тригонометрических неравенств с помощью единичной окружности

ГБОУ СОШ № 000 с углубленным изучением английского языка Адмиралтейского района Санкт-Петербурга

Решение тригонометрических неравенств с помощью единичной окружности

Тригонометрические неравенства одна из самых сложных тем в школьном курсе математики. При решении простейших тригонометрических неравенств удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и верно записать множества решений данного неравенства.

Цель данной разработки — сформировать у школьников умения использовать тригонометрический круг при решении простейших неравенств вида sin x > a, sin x a, cosx , называются тригонометрическими неравенствами.

Решить тригонометрическое неравенство — это значит, найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется.

Тригонометрические неравенства можно решать с помощью графиков функций y = sin x, y = cos x, y = tg x, y= ctg x или с помощью единичной окружности.

Решение тригонометрических неравенств, сводится, как правило, к решению простейших неравенств вида: sin x>a, sin xa, sin xa, sin x

Алгоритм решения тригонометрических неравенств

с помощью единичной окружности.

1) На оси ординат (абсцисс) отметить точку a и провести прямую y = a (x = a), перпендикулярную соответствующей оси.

2) Отметить на окружности дугу, состоящую из точек окружности, удовлетворяющих данному неравенству (эти точки расположены по одну сторону от построенной прямой).

3) Записать числовой промежуток, точки которого заполняют отмеченную дугу, и к обеим частям неравенства прибавить период функции ( для y = sin x и y = cos x ).

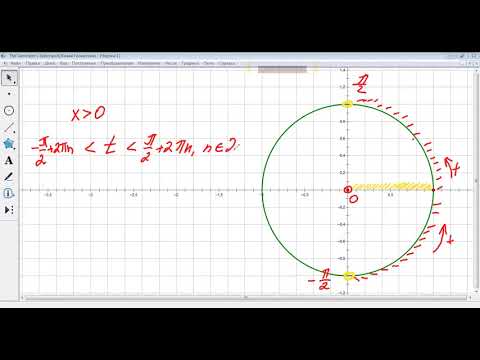
Решение простейших неравенств вида sin x>a, sin xa, sin xa, sin x

На единичной окружности проводим прямую y = , которая пересекает окружность в точках A и B.

Все значения y на промежутке NM больше , все точки дуги AMB удовлетворяют данному неравенству. При всех углах поворота, больших , но меньших , sin x будет принимать значения больше (но не больше единицы).

Таким образом, решением неравенства будут все значения на интервале , т. е. a, cos xa, cos xa, cos x

💥 Видео

Координаты точек на числовой окружности, часть 2. Алгебра 10 класс.Скачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

Решение неравенства методом интерваловСкачать

Изобразить область на комплексной плоскостиСкачать