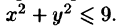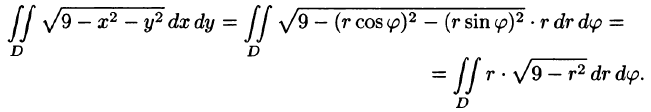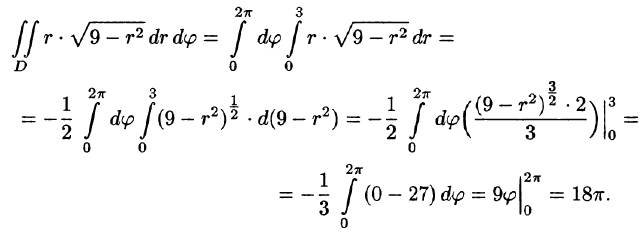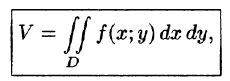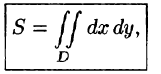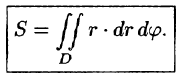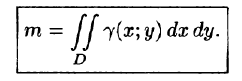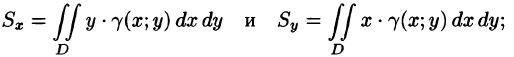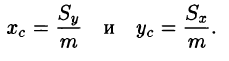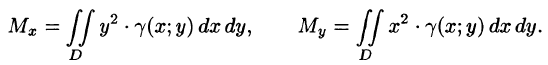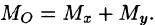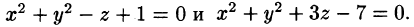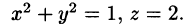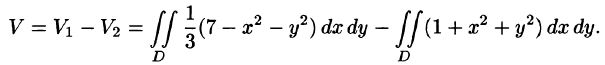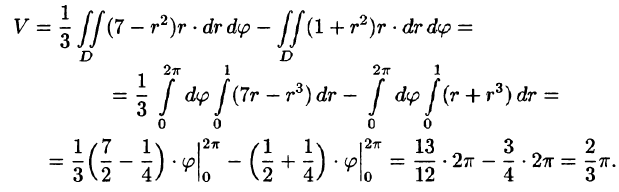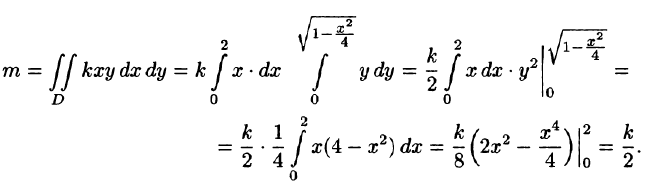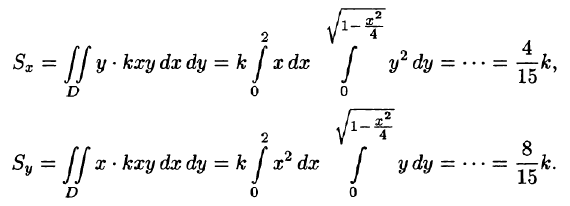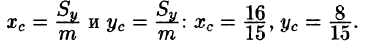- Что значит вычислить двойной интеграл?
- Сведение двойного интеграла к повторному
- Случай прямоугольной области
- Случай криволинейной или треугольной области
- Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
- x-правильная и неправильная, y-правильная и неправильная области интегрирования
- Смена порядка интегрирования
- Вычисление площади и объёма с помощью двойных интегралов
- Так что же такое двойной интеграл?
- Двойной интеграл с примерами решения и образцами выполнения
- Геометрический и физический смысл двойного интеграла
- Масса плоской пластинки
- Основные свойства двойного интеграла
- Вычисление двойного интеграла в декартовых координатах
- Вычисление двойного интеграла в полярных координатах
- Приложения двойного интеграла
- Объем тела
- Площадь плоской фигуры
- Масса плоской фигуры
- Статические моменты и координаты центра тяжести плоской фигуры
- Моменты инерции плоской фигуры
- Двойной интеграл
- Как взять двойной интеграл по окружности
- 💡 Видео
Видео:Двойной интеграл / Как находить двойной интеграл через повторный (двукратный) / Два способаСкачать
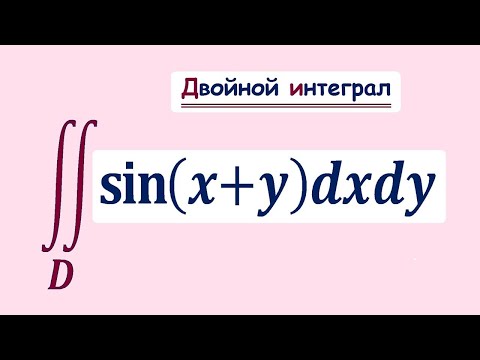
Что значит вычислить двойной интеграл?
Двойные интегралы – это обобщение понятия определённого интеграла для функции двух переменных, заданной как z = f(x, y) .
Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.
Вычислить двойной интеграл — значит найти число, равное площади упомянутой фигуры D .
Пока мы не касаемся определения двойного интеграла, а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .
В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D — криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.
Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.
Случай прямоугольной области:
Случай криволинейной области:
А это уже решение знакомых нам определённых интегралов, в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.
Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Сведение двойного интеграла к повторному
Случай прямоугольной области
Пусть дана функция двух переменных f(x, y) и ограничения для D : D = <(x; y) | a ≤ x ≤ b; c ≤ y ≤ d> , означающие, что фигуру D слева и справа ограничивают прямые x = a и x = b , а снизу и сверху — прямые y = c и y = d . Здесь a, b, c, d — числа.
Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Здесь пределы интегрирования a, b, c, d — числа, о которых только что упоминалось.
Сначала нужно вычислять внутренний (правый) определённый интеграл, затем — внешний (левый) определённый интеграл.
Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид

Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 1. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая игрек константой. Пользуемся формулой 7 из таблицы интегралов. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого), пользуясь для каждого слагаемого той же формулой 7:
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Случай криволинейной или треугольной области
Пусть снова дана функция двух переменных f(x, y) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области — прямые x = a и x = b , но снизу и сверху — кривые, которые заданы уравнениями 



Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Здесь пределы интегрирования a и b — числа, а 



Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем — левый определённый интеграл.
Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид

Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 3. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования и видим, что она треугольная:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

Вычисляем первое слагаемое:
Вычисляем второе слагаемое:
Вычисляем третье слагаемое:
Получаем сумму, которая и будет решением данного двойного интеграла:

Пример 4. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Видео:Двойной интеграл в полярных координатахСкачать

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
Пример 5. Вычислить двойной интеграл

если область D ограничена прямыми

Пример 6. Вычислить двойной интеграл

если область D ограничена прямыми

Видео:Вычислить двойной интеграл, перейдя к полярным координатамСкачать

x-правильная и неправильная, y-правильная и неправильная области интегрирования
Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:
1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;
2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.
Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x-правильной
Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.
До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.
Пример 7. Вычислить двойной интеграл 
Решение. Область интегрирования является y-неправильной, так как её нижнюю границу нельзя задать одной линией y = y(x) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части — 

Вычисляется этот двойной интеграл так:
Видео:Математика без ху!ни. Двойные интегралы. Часть1. Как вычислять.Скачать

Смена порядка интегрирования
Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.
Смена порядка интегрирования образно может быть описана следующими словами О’Генри: «Так ведёт себя обитатель джунглей — зверь, попав в клетку, и так ведёт себя обитатель клетки — человек, заблудившись в джунглях сомнений». Результат, так же по О’Генри один и тот же: «Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд». (О’Генри. Шехерезада с Мэдисон-сквера.)
Тогда, если левый интеграл у нас по переменной x, а правый — по y, то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для «нового» игрека нужно «позаимствовать» у «старого» икса, а пределы интегрирования для «нового» икса получить в виде обратной функции, разрешив относительно икса уравнение, задававшее предел для игрека.
Пример 8. Сменить порядок интегрирования для повторного интеграла

Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу — правым. Пределы интегрирования для «нового» игрека позаимствуем у «старого» икса, то есть нижний предел равен нулю, а верхний — единице. Пределы интегрирования для «старого» игрека заданы уравнениями 



Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.
Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.
Пример 9. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .
При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x/2 , что видно на рисунке ниже.
Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.
Пример 10. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми 

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.
Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Для 
Для 
Для 
Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:
Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.
И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге — расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла — таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и — почти на автомате — на разбиении области и опустим само решение.
Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:
Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:
Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y-неправильной, так как её верхнюю границу нельзя задать одной линией y = y(x) .
Поэтому разобьём область интегрирования на две части при помощи прямой x = 1 (на чертеже — чёрного цвета).
Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:

Видео:Объем через двойной интегралСкачать
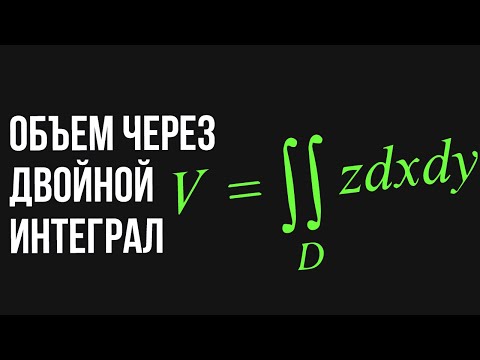
Вычисление площади и объёма с помощью двойных интегралов
В этом параграфе даны примеры, в которых двойной интеграл равен отрицательному числу. Но, как отмечалось в теоретической справке в начале урока, площадь области интегрирования равна самому двойному интегралу. А если двойной интеграл — отрицательное число, то площадь равна его модулю.
Вычисление площади плоской фигуры с помощью двойного интеграла имеет более универсальный характер, чем вычисление площади криволинейной трапеции с помощью определённого интеграла. С помощью двойного интеграла можно вычислять площади не только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к к координатным осям.
Пример 12. Вычислить площадь области, ограниченной линиями y² = x + 1 и x + y = 1 .
Решение. Область интегрирования представляет собой фигуру, ограниченную слева параболой y² = x + 1 , а справа прямой y = 1 — x . (рисунок ниже).
Решая как систему уравнения этих линий, получаем точки их пересечения: 

Вычисляем внутренний (правый) интеграл:

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Как видим, решение двойного интеграла — отрицательное число. За площадь данной плоской фигуры принимается модуль этого числа, то есть 4/9.
Объём криволинейного цилиндра, ограниченного сверху поверхностью 
Пример 13. Вычислить объём тела, ограниченного поверхностями x = 0 , y = 0 , z = 0 и x + y + z = 1 (рисунок ниже).
Расставляя пределы интегрирования, получаем следующий повторный интеграл:

Вычисляем внутренний (правый) интеграл:

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Вновь видим, что решение двойного интеграла — отрицательное число. За объём данного тела принимается модуль этого числа, то есть 1/6.
Видео:Изменение порядка интегрирования в повторном интегралеСкачать

Так что же такое двойной интеграл?
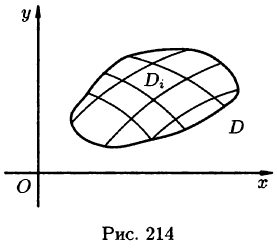
Мы уже знаем, что представляет собой область D. Пусть z = f(x, y) — некоторая функция двух переменных, определённая и ограниченная в этой области. Разобъём область D произвольно на n частей, не имеющих общих точек, с площадями 


которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.
Определение. Если интегральная сумма при неограниченном возрастании числа n разбиений области D и стремлении наибольшего из диаметров частичных областей к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. Обобщением понятия двойного интеграла для функции трёх переменных является тройной интеграл.
Видео:Математический анализ, 41 урок, Вычисление двойных интеграловСкачать

Двойной интеграл с примерами решения и образцами выполнения
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
Пусть в замкнутой облас
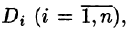

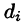
В каждой области 
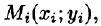
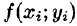

Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 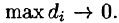
Таким образом, двойной интеграл определяется равенством
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
- Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям (см. рис. 215). При этом
равенство (53.2) можно записать в виде
Видео:18. Признаки сравнения несобственных интегралов 2 рода (первый признак)Скачать

Геометрический и физический смысл двойного интеграла
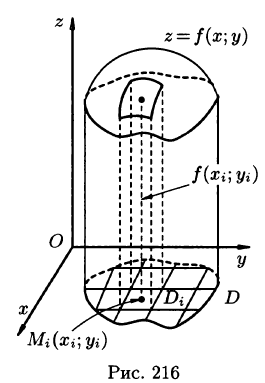
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
Рассмотрим тело, ограниченное сверху поверхностью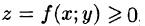

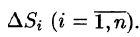

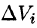
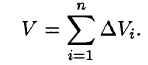
Возьмем на каждой площадке Di произвольную точку 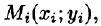

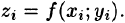
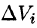
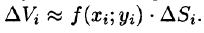
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей» 

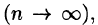
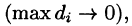
или, согласно равенству (53.2),
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 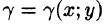
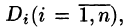


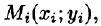
Если области D, достаточно малы, то плотность в каждой точке 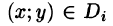
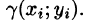

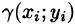
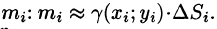
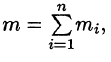
Точное значение массы получим как предел суммы (53.5) при условии
или, согласно равенству (53.2),
Итак, двойной интеграл от функции 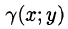
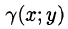
Видео:Топ метод вычисления интегралов. Формула интегрирования по частям. Высшая математикаСкачать

Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
3.Если область D разбить линией на две области 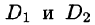
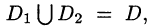
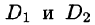
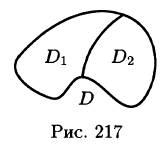
4.Если в области D имеет место неравенство 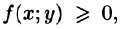
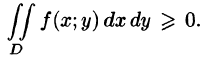
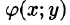
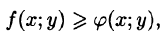
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 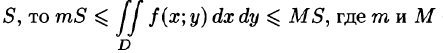
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка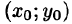
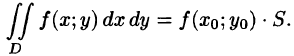
называют средним значением функции f(x; у) в области D.
Видео:Площадь круга через интегралСкачать

Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 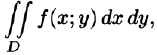
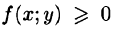
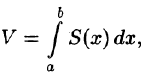
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
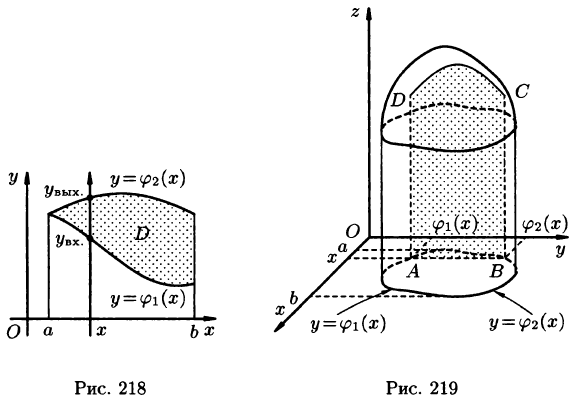
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми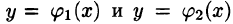
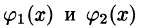
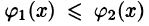
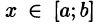
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
Площадь S(x) этой трапеции находим с помощью определенного интеграла
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 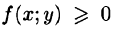
Это равенство обычно записывается в виде
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 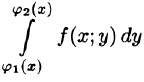
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми 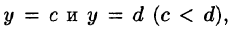
для всех 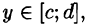
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
- Формулы (53.7) и (53.8) справедливы и в случае, когда
- Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
- Если область D не является правильной ни «по x», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении осиОх или оси Оу.
- Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример:
Вычислить 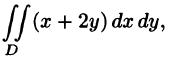
Решение:
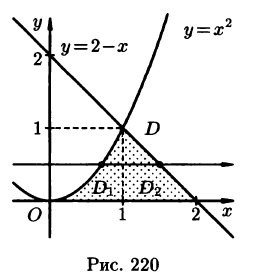
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
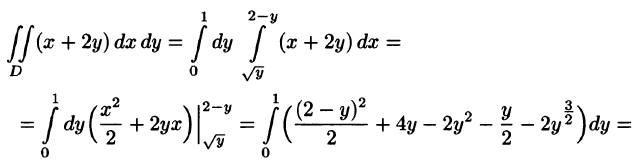
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: 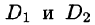
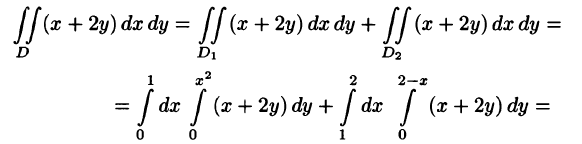
Ответ, разумеется, один и тот же.
Видео:Двойные интегралы в полярных координатахСкачать

Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель
а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
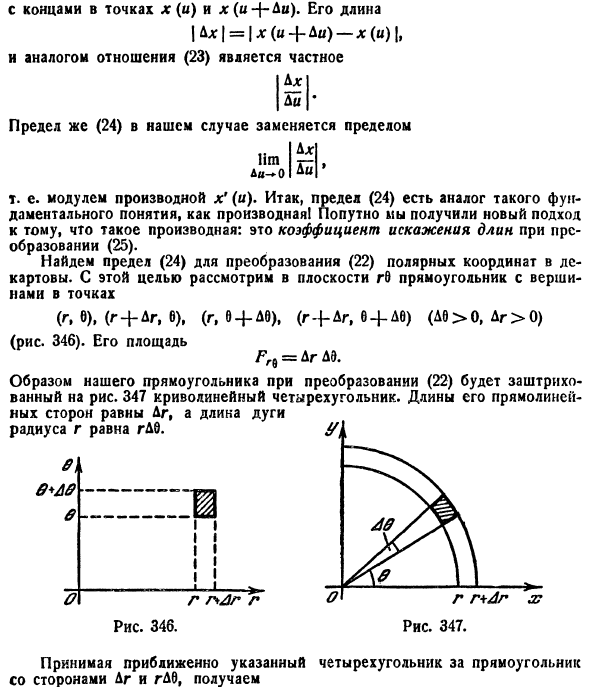
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами
В качестве инь возьмем полярные координаты 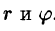
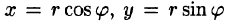
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
Формула замены переменных (53.11) принимает вид:
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
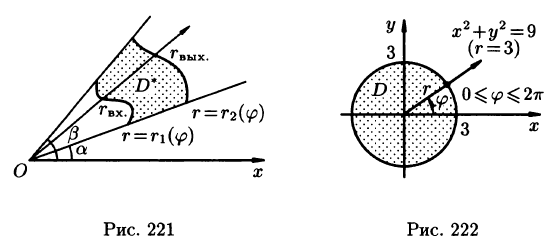
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами 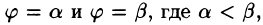
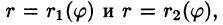
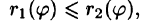
Внутренний интеграл берется при постоянном
Замечания:
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
область Dесть круг, кольцо или часть таковых.
- На практике переход к полярным координатам осуществляется путем замены
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
(исследуя закон изменения
точки
при ее отождествлении с точкой (х; у) области D).
Пример:
Вычислить 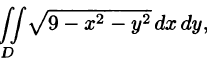
Решение: Применив формулу (53.12), перейдем к полярным координатам:
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 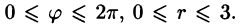
Видео:Перейти к полярным координатам в двойном интегралеСкачать

Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
или, в полярных координатах,
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 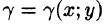
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
а координаты центра масс фигуры по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 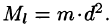
Момент инерции фигуры относительно начала координат — по формуле
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример:
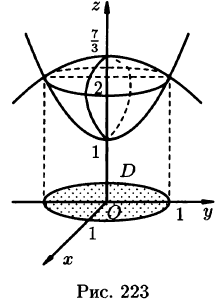
Найти объем тела, ограниченного поверхностями
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
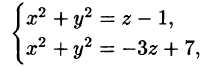
находим уравнение линии их пересечения:
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 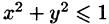
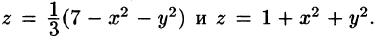
Переходя к полярным координатам, находим:
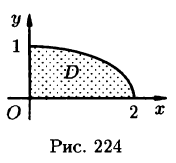
Пример:
Найти массу, статические моменты 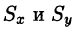
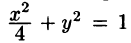
Решение: По формуле (53.6) находим массу пластинки. По условию, 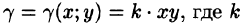
Находим статические моменты пластинки:
Находим координаты центра тяжести пластинки, используя формулы
Видео:Криволинейная трапеция и ее площадь. 11 класс.Скачать

Двойной интеграл












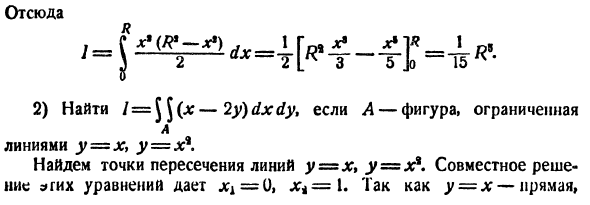

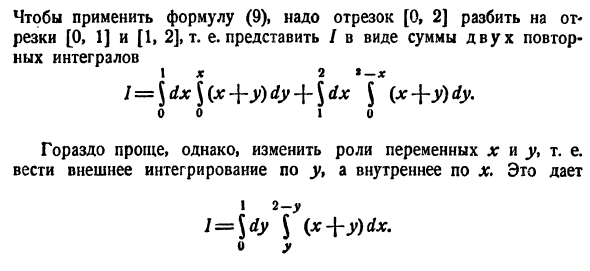

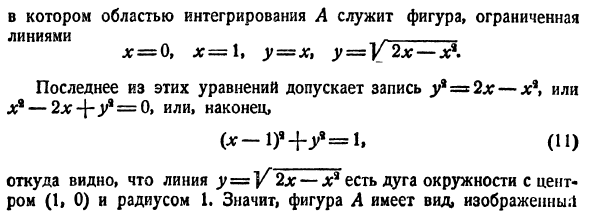














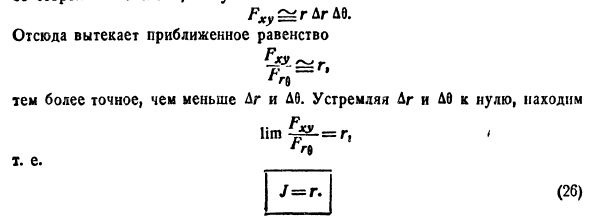


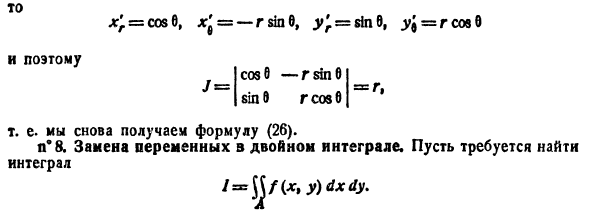

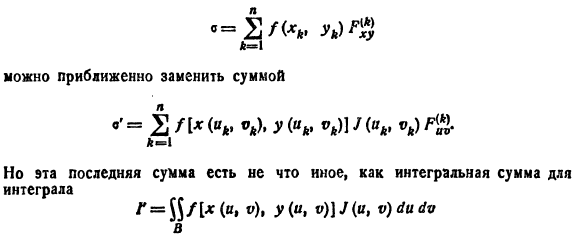








Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Вычислить двойной интеграл по области, ограниченной линиями ∫∫(5x+y)dxdy D: y=x^3, y=0, x=3.Скачать

Как взять двойной интеграл по окружности
В двойном интеграле , где G — круг, ограниченный окружностью x 2 + y 2 = 2x, перейти к полярным координатам с полюсом в точке O(0, 0) и вычислить полученный интеграл.
Круг G изображен на Рис. 1, а.
Уравнения, связывающие ( x, y) и полярные координаты ( ρ, φ) с полюсом в точке O(0, 0), имеют вид
причем наглядно видно, что в качестве промежутка изменения φ можно взять сегмент —π/2 ≤ φ ≤ π/2. Подставляя выражения (1) в уравнение окружности, получим ρ 2 = 2ρ cos φ, откуда ρ = 0 или ρ = 2 cos φ. Эти две кривые на плоскости (ρ, φ) при —π/2 ≤ φ ≤ π/2 ограничивают область g (см. Рис. 1, б), являющуюся прообразом области G при отображении (1). Якобиан отображения (1) равен ρ. Отметим, что
на границе ρ = 0 области g, однако формула
(2)
замены переменных применима. Подынтегральная функция x 2 + y 2 в новых переменных равна ρ 2 . По формуле (2) имеем
Полученный двойной интеграл по области g сводим к повторному:
(3)
и вычисляем повторный интеграл, применяя формулу Ньютона-Лейбница:
Замечание 1. Расстановку пределов интегрирования в повторном интеграле (3) можно произвести, рассматривая не область g, а изменение полярных координат в исходной области G. На Рис. 1(в) видно, что при каждом значении φ из промежутка [-π/2, π/2] переменная ρ изменяется от 0 (значение ρ в полюсе) до 2 cos φ (значение ρ на окружности, уравнение которой в полярных координатах имеет вид ρ = 2 cos φ). Таким образом, пределы интегрирования по φ — от —π/2 до π/2, а по ρ — от 0 до 2 cos φ.
Замечание 2. Обычно замена переменных в двойном интеграле производится с целью упрощения области интегрирования. Если в данном примере перейти к полярным координатам с полюсом не в точке O(0, 0), а в точке A(1, 0) (центре круга), т. е. по формулам x — 1 = ρ cos φ, y = ρ sin φ, то прообразом круга G окажется прямоугольник (наиболее простая область) σ = <(ρ, φ): 0 ≤ ρ ≤ 1, 0 ≤ φ ≤ 2π> (см. Рис. 1, г). Выражение для подынтегральной функции примет вид x 2 + y 2 = 1 + 2ρ cos φ + ρ 2 . В этом случае, используя формулу (2) и сводя двойной интеграл к повторному, получим
💡 Видео
Семинар 4. Двойной интеграл.Скачать

Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Двойной интеграл (ч.25). Вычисление в полярных координатах. Высшая математика.Скачать

Двойной интеграл. Вычисление в полярных координатахСкачать

ТФКП. ИНТЕГРАЛ ПО ДУГЕ ОКРУЖНОСТИ от неаналитической функции. Метод замены переменной.Скачать




























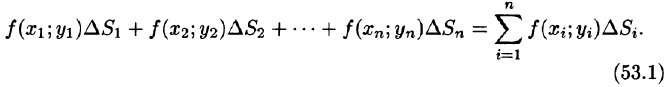
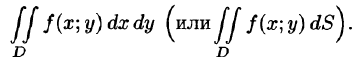
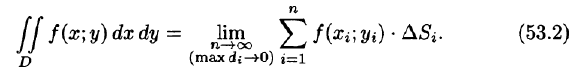
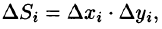 равенство (53.2) можно записать в виде
равенство (53.2) можно записать в виде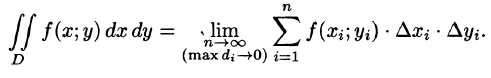
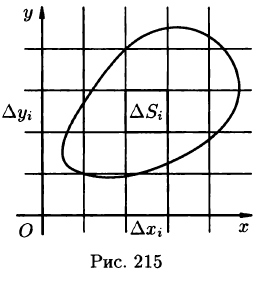

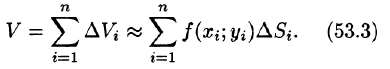
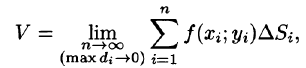
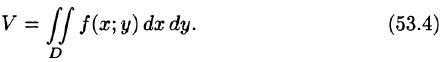
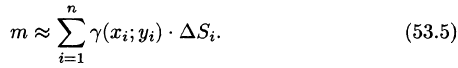
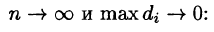
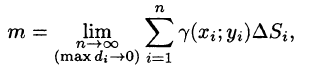
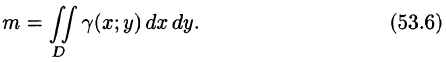
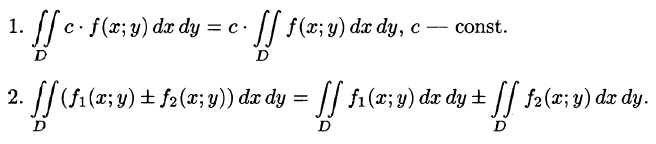
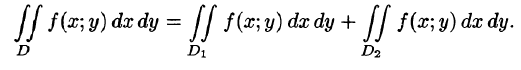
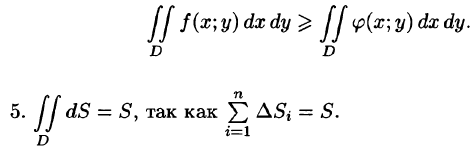
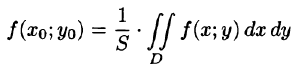
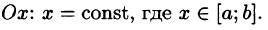
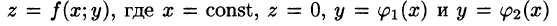
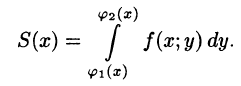
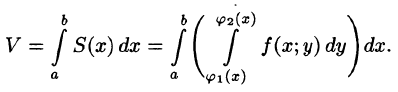
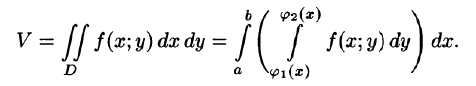
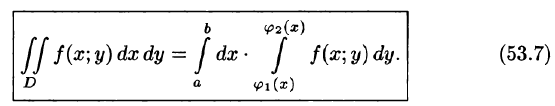
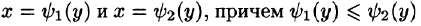
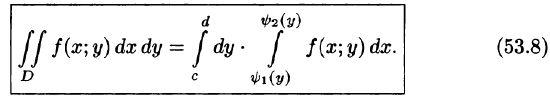
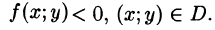
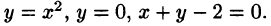
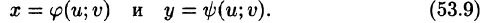

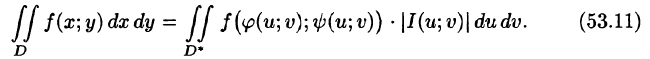
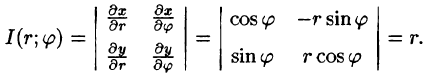
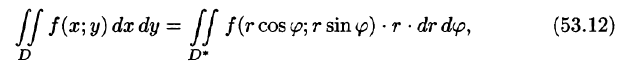
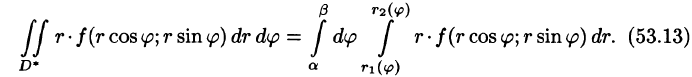
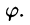
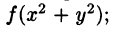 область Dесть круг, кольцо или часть таковых.
область Dесть круг, кольцо или часть таковых.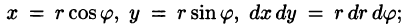 уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по 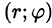 при ее отождествлении с точкой (х; у) области D).
при ее отождествлении с точкой (х; у) области D).