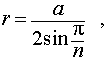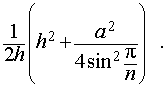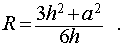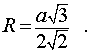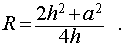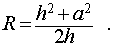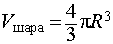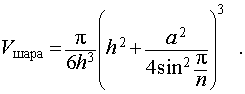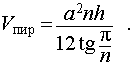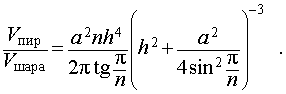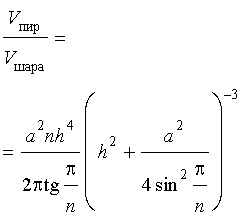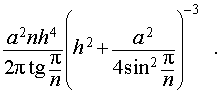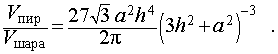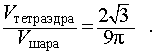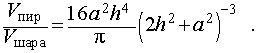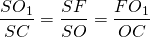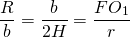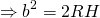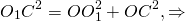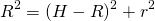Как вписать пирамиду в окружность

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

Радиус сферы, описанной около правильной n — угольной пирамиды

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

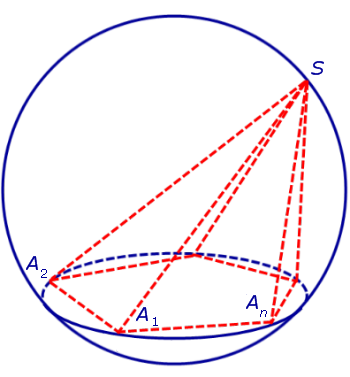
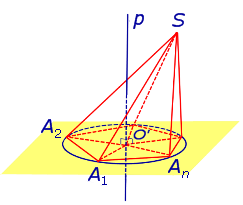
Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.

Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

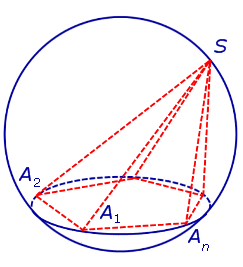
На рисунке 2 изображена пирамида SA₁A₂ . A_n , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A₁A₂ . A_n – основание пирамиды. Доказано.

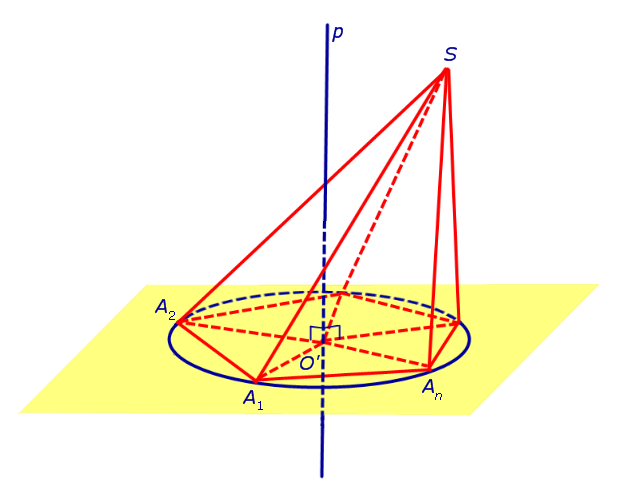
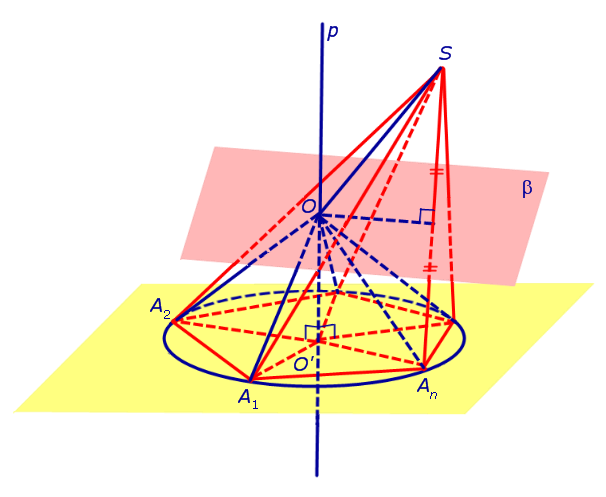
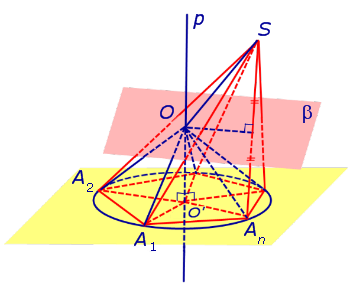
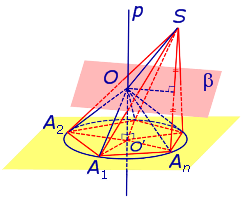
Теперь предположим, что около основания A₁A₂ . A_n пирамиды SA₁A₂ . A_n можно описать окружность. Докажем, что в этом случае около пирамиды SA₁A₂ . A_n можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A₁A₂ . A_n , символом O’ и проведем прямую p, проходящую через точку O’ и перпендикулярную к плоскости многоугольника A₁A₂ . A_n (рис. 3).

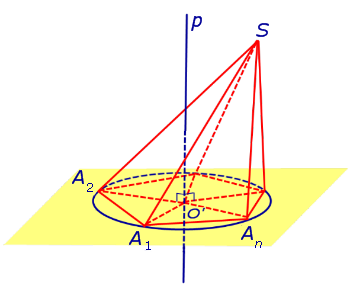
Рассмотрим плоскость β, проходящую через середину отрезка SA_n и перпендикулярную к этому отрезку. Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA₁A₂ . A_n . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.

Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA₁A₂ . A_n . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA₁A₂ . A_n .

Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A₁A₂ . A_n , что противоречит определению пирамиды.

Следствие 1. Около любой правильной пирамиды можно описать сферу.

Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.

Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.

Видео:Вычисление радиуса сферы, вписанной в правильную треугольную пирамидуСкачать

Радиус сферы, описанной около правильной n — угольной пирамиды

Задача 1. Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.

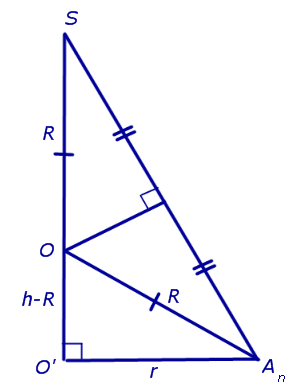
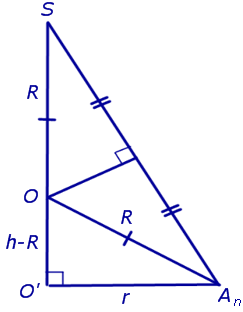
Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’A_n (рис. 5).

Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OA_n получаем

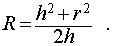(1)

из формулы (1) получаем соотношение

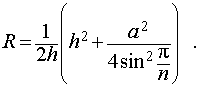(2)

Ответ.

Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен

Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен

Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен

Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен

Видео:Пирамида и шар. Практическая часть. 11 класс.Скачать

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Задача 2. Около правильной n — угольной пирамиды с высотой h и ребром основания a описана сфера. Найти отношение объемов пирамиды и шара, ограниченного сферой, описанной около данной пирамиды.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около пирамиды сферой, через высоту и ребро основания пирамиды:

Ответ.

Следствие 7. Отношение объема правильной треугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной пирамиды, равно

Следствие 8. Отношение объема правильного тетраэдр с ребром a к объему шара, ограниченного сферой, описанной около данного тетраэдра, равно

Следствие 9. Отношение объема правильной четырехугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 10. Отношение объема правильной шестиугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Видео:Шар, вписанный в пирамиду, или пирамида, описанная около шара.Скачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Вписанная в шар пирамида

Когда в задаче дана вписанная в шар пирамида, при ее решении будет полезна следующая теоретическая информация.

Если пирамида вписана в шар, то все ее вершины лежат на поверхности этого шара (на сфере), соответственно, расстояния от центра шара до вершин равны радиусу шара.

Каждая грань вписанной в шар пирамиды является вписанным в некоторую окружность многоугольником. Основания перпендикуляров, опущенных из центра шара на плоскости граней, являются центрами этих описанных окружностей. Таким образом, центр описанного около пирамиды шара — точка пересечения перпендикуляров к граням пирамиды, проведенных через центры описанных около граней окружностей.

Чаще центр описанного около пирамиды шара рассматривают как точку пересечения перпендикуляра, проведенного к основанию через центр описанной около основания окружности, и серединного перпендикуляра к боковому ребру (серединный перпендикуляр лежит в плоскости, проходящей через это боковое ребро и первый перпендикуляр (проведенный к основанию). Если около основания пирамиды нельзя описать окружность, то эта пирамида не может быть вписана в шар. Отсюда следует, что около треугольной пирамиды всегда можно описать шар, а вписанная в шар четырехугольная пирамида с параллелограммом в основании может иметь основанием прямоугольник либо квадрат.

Центр описанного около пирамиды шара может лежать внутри пирамиды, на поверхности пирамиды (на боковой грани, на основании), и вне пирамиды. Если в условии задачи не сказано, где именно лежит центр описанного шара, желательно рассмотреть, как могут повлиять на решение различные варианты его расположения.

Около любой правильной пирамиды можно описать шар. Его центр — точка пересечения прямой, содержащей высоту пирамиды, и серединного перпендикуляра к боковому ребру.

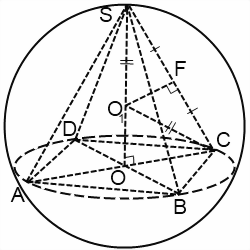
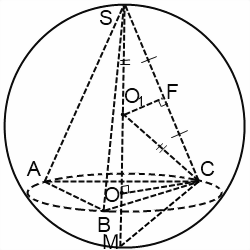
При решении задач на вписанную в шар пирамиду чаще всего рассматривают некоторые треугольники.

Начнем с треугольника SO1C. Он равнобедренный, поскольку две его стороны равны как радиусы шара: SO1=O1С=R. Следовательно, O1F — его высота, медиана и биссектриса.

Прямоугольные треугольники SOC и SFO1 подобны по острому углу S. Отсюда

SO=H — высота пирамиды, SC=b — длина бокового ребра, SF=b/2, SO1=R, OC=r — радиус окружности, описанной около основания пирамиды.

В прямоугольном треугольнике OO1C г гипотенуза O1C=R, катеты OC=r, OO1=H-R. По теореме Пифагора:

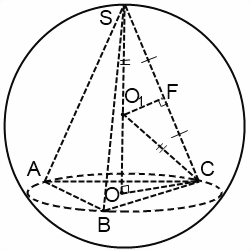
Если продолжить высоту SO, получим диаметр SM. Треугольник SCM — прямоугольный (так как вписанный угол SCM опирается на диаметр). В нем OC — высота, проведенная к гипотенузе, SO и OM — проекции катетов SC и CM на гипотенузу. По свойствам прямоугольного треугольника,

и еще раз, только другим путем:

Эти рассуждения верны не только для правильной пирамиды, но также для пирамиды , основание высоты которой является центром описанной около основания пирамиды окружности.

Видео:ПРАВИЛЬНЫЙ РАЗБОЙ ПИРАМИДЫ В РУССКОМ БИЛЬЯРДЕСкачать

Нахождение радиуса шара (сферы), вписанного в правильную пирамиду

В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.

Видео:Быстро находим радиус описанной сферыСкачать

Формулы расчета радиуса шара (сферы)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;

Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:

Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

Правильная четырехугольная пирамида

• a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
• EF – высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается так:

Правильная шестиугольная пирамида

• a – ребро основания пирамиды, т.е. AB, BC, CD, DE, EF, AF;
• GL – высота пирамиды (h).

Радиус (r) вписанного шара/сферы вычисляется по формуле:

📺 Видео

Шар, вписанный в усеченную пирамиду.A ball inscribed in a truncated pyramid.Скачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Решение C2 - сфера, вписанная в пирамиду. Подготовка к ЕГЭ по математике 2014Скачать

Развертка пирамидыСкачать

Как нарисовать пирамиду?Скачать

Построение пятиугольника циркулемСкачать

ПРАВИЛА БИЛЬЯРДА: Русский бильярд для начинающих - расстановка шаров, разбой пирамиды, штрафыСкачать

Урок-1 по Невке. Построение серий в динамичную пирамиду.Скачать

Пирамида, вписанная в шар, или, шар, описанный около пирамиды.Скачать

Шестиугольник в изометрииСкачать

Как создать ШАР \ ПИРАМИДУ \ КОНУС в Компас 3D v20 homeСкачать

Шар, вписанный в правильную треугольную пирамидуСкачать

ЕГЭ Задание 14 Пирамида вписана в сферуСкачать