Как сравнивать стороны треугольников (4 видео)

Геометрия. 7 класс

Конспект урока

Соотношения между сторонами и углами треугольника. Неравенство треугольника

Перечень рассматриваемых вопросов:

Установление соотношений между сторонами и углами треугольника.
Формулирование неравенства треугольника.
Теоремы о сравнении сторон и углов треугольника, их применение при решении задач.
Проведение исследования о существовании треугольника с заданными элементами.

Каждая сторона треугольника меньше суммы двух других сторон.

В треугольнике против большей стороны лежит больший угол. Против большего угла лежит большая сторона.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее, на уроках геометрии, вы познакомились с различными фигурами, в том числе и с треугольником.

Сегодня мы продолжим изучать треугольники и рассмотрим соотношение между его элементами.

Теорема: В треугольнике против большей стороны лежит больший угол.

Отложим на стороне AB отрезок, равный стороне AC.

Угол 2 – внешний угол треугольника BDC, поэтому ∠2 > ∠B (по свойству внешнего угла треугольника).

∠1 = ∠2 как углы при основании равнобедренного ∆ADC (по свойству равнобедренного треугольника).

Справедлива и теорема, обратная данной. Против большего угла лежит большая сторона.

Предположим, что АВ = АС или АВ ∠ В.

Поэтому наше предположение неверное → AB > AC.

Докажем два следствия из этих теорем.

1 следствие. В прямоугольном треугольнике гипотенуза больше катета.

Дано: ∆АВС – прямоугольный.

Доказательство: ∠В > ∠А, т. к. ∠В = 90° ( по условию), ∠А –острый → АС > СВ (по обратной теореме о соотношениях между сторонами и углами треугольника: против большего угла лежит большая сторона).

Что и требовалось доказать.

Докажем второе следствие из этих теорем.

Если два угла треугольника равны, то треугольник равнобедренный. Это следствие называется признак равнобедренного треугольника.

Доказать: ∆АВС – равнобедренный

Докажем, что АВ = ВС.

Пусть АВ > ВС →∠С > ∠А (по теореме доказанной выше: против большей стороны лежит больший угол), противоречит условию, т. к. ∠А = ∠С . → АВ = ВС →∆АВС – равнобедренный (по определению равнобедренного треугольника).

Что и требовалось доказать.

Докажем теорему по соотношению между сторонами треугольника.

Каждая сторона треугольника меньше суммы двух других сторон.

Доказать: АВ ∠1 (так как угол 1 часть угла АВD), →∠ABD > ∠2 (так как ∠1 = ∠2).

Так как против большего угла лежит большая сторона (по теореме о соотношениях между сторонами и углами треугольника) → AB ВН (по обратной теореме о соотношениях между сторонами и углами треугольника).

Рассмотрим ещё случай АВ = ВС → ∆АВС – равнобедренный (по определению равнобедренного треугольника). То ВМ = ВН (по свойству равнобедренного треуголника, высота и медиана совпадают, если проведены к его основанию)→ ВМ ≥ ВН.

Что и требовалось доказать.

Разбор заданий тренировочного модуля.

1 Дано: ABC, равнобедренный, вычислите чему равна третья сторона треугольника, если две других равны 8 см и 4 см?

Объяснение: По определению равнобедренного треугольника, две его боковые стороны равны, следовательно это будет сторона равная 4 см или 8см.

Сторона 4см не может быть, т. к. 8см = 4 см + 4 см., что противоречит теореме о соотношениях между сторонами треугольника: каждая сторона треугольника меньше суммы двух других сторон.

Предположим, что боковые стороны равны 8 см. Тогда, по теореме о соотношениях между сторонами треугольника, каждая сторона треугольника меньше суммы двух других сторон, получим следующее соотношение между сторонами треугольника:

Видео:Признаки равенства треугольников. 7 класс.Скачать

Треугольник. Соотношения между углами и сторонами треугольника.

Теорема.

Если любую сторону треугольника продолжить в одном направлении, то образовавшийся при этом внешний угол больше каждого внутреннего угла, не смежного с ним.

Следствие из теоремы.

Если в треугольнике один из углов прямой или тупой, то два других угла будут острые.

Теорема. В любом треугольнике:

1. Напротив равных сторон расположены одинаковые углы.

2. Напротив большей стороны расположен больший угол.

Следствия из теоремы.

2. В разностороннем треугольнике одинаковых углов нет.

Обратные теоремы. В каждом треугольнике:

1. Напротив одинаковых углов расположены одинаковые стороны.

2. Напротив большего угла расположена большая сторона.

Следствия

1. Равноугольный треугольник является и равносторонним.

2. В треугольнике сторона, расположенная напротив тупого или прямого угла, больше других сторон.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Математика

85. Построим равнобедренный ∆ABC (чер. 92), у которого AB = BC. Тогда мы знаем, что его углы при основании равны, т. е. ∠A = ∠C. Пронумеруем эти углы, – тогда ∠1 = ∠2. Станем теперь строить новые треугольники ABC’, ABC» и т. д. так, чтобы сторона AB и ∠B оставались неизменными, но сторона BC увеличивалась. Тогда угол A должен увеличиваться (что очевидно), а угол C станет уменьшаться: мы видим, что ∠3 ∠3 или ∠3 ∠4 или ∠4 1) Если в треугольнике две стороны равны, то против них лежат равные углы.

2) Если в треугольнике две стороны не равны, то против большей из них лежит и больший угол.

86. Теперь, наоборот, построим: 1) треугольник с двумя равными углами и 2) треугольник с двумя неравными углами и сравним стороны, противолежащие этим углам. Для решения вопросов, здесь возникающих, воспользуемся способом рассуждения, часто употребляемым в математике.

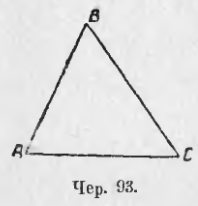
1) Пусть ∆ABC (чер. 93) постоен так, что ∠A = ∠C. Сравнить стороны BC и BA.

Пока, не зная ничего про стороны AB и BC, мы можем сделать об них 3 предположения: 1) AB = BC, 2) AB > BC и 3) AB BC должно, на основании предыдущего п., повлечь за собою следствие, что ∠C > ∠A, а у нас построено: ∠C = ∠A. Следовательно, это предположение должно быть вычеркнуто. Также из 3-го предположения, что AB ∠C, что также противоречит нашему построению. Следовательно, и это предположение должно быть вычеркнуто. Остается поэтому лишь одно предположение, что AB = BC, которое и должно быть верно, так как иных сделать нельзя. Поэтому имеем:

Если в треугольнике два угла равны, то против них лежат равные стороны.

2) Пусть ∆ABC (чер. 93) постоен так, что ∠A > ∠C. Сравнить стороны BA и BC.
Опять мы можем сделать 3 предположения: 1) AB = BC, 2) AB > BC и 3) AB BC не годится, так как из него вытекало бы, что ∠C > ∠A, что противоречит построению. Остается лишь 3-е предположение, что AB Если два угла в треугольнике неравны, то против большего из них лежит большая сторона.

Теперь легко решаются вопросы: 1) какая из сторон прямоугольного треугольника самая большая? 2) Какая из сторон тупоугольного треугольника самая большая?

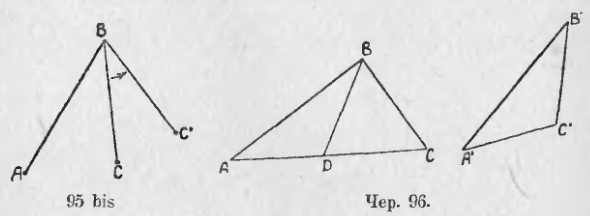
87. В двух предыдущих пп. мы имели дело с двумя положениями: 1) против большей стороны лежит больший угол и 2) против большего угла лежит большая сторона. Мы нашли, что эти мысли справедливы для одного треугольника. Возникает вопрос, справедливы ли они для двух треугольников ? Несомненно справедливы для двух равных треугольников , так как равные треугольники можно наложением слить в один треугольник. Но, вообще говоря, к двум различным (не равным) треугольникам эти положения не могут быть применимы: мы можем построить два таких треугольника ∆ABC и ∆A’B’C’ (чер. 94), чтобы ∠B был > ∠B’, но AC была бы Этот случай легко уясняется наглядно. Возьмем две палочки AB и BC (чер. 95 bis) и сложим их концами (в точке B). Если вращать палочку BC около точки B по стрелке, то ∠B станет увеличиваться: сторона BC будет менять свое положение (пусть одно из них есть BC’), но все время BC останется равным самому себе; не изменяется также и отрезок AB. Обратим внимание, что точками A и C определяется еще отрезок AC, на чертеже не изображенный. При вышеуказанном вращении точка C меняет свое место и нам ясно, что этот отрезок AC, не изображенный на чертеже, должен увеличиваться (напр. AC’ > AC), т. е., если 2 стороны треугольника не изменяются, а угол между ними увеличивается, то третья сторона так же увеличивается. В тексте этот случай выяснен без помощи такого наглядного представления.

Построим два таких треугольника, чтобы у них было по две равных стороны, но чтобы углы между ними не были равны. Пусть в ∆ABC и в ∆A’B’C’ (чер. 95) имеем AB = A’B’, BC = B’C’, но ∠B > ∠B’. Сравним стороны AC и A’C’, лежащие против неравных углов. Для этого наложим ∆A’B’C’ на ∆ABC так, чтобы сторона A’B’ совпала с равною ей стороною AB. Тогда сторона B’C’ должна пойти внутри ∠B, потому что ∠B’ отмеченного угла BDC при основании равнобедренного треугольника. Но ∠BCD = ∠BDC, следовательно, ∠ADC > ∠ACD. Поэтому на основании п. 86 (применяя его к ∆ACD) имеем AC > AD, но AD есть сторона A’C’, перенесенная в другое место, – следовательно, AC > A’C’.

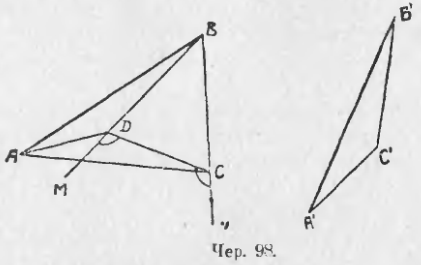
3) Пусть ∆A’B’C’ при наложении займет положение ∆ABD (чер. 98), т. е. точка C’ расположится внутри ∆ABC. Тогда, соединив точки C и D, получим равнобедренный ∆CBD (BD = BC, ибо BD есть сторона B’C’, перенесенная в другое положение, а B’C’ = BC по построению) и, следовательно, ∠BCD = ∠BDC. Если продолжить стороны BD и BC по направлениям DM и CN, то получим два внешних угла этого равнобедренного треугольника ∠MDC и ∠NCD, но ∠MDC = ∠NCD, следовательно, ∠ADC > ∠ACD, а поэтому, на основании п. 86, имеем AC > AD, или AC > A’C’ (AD есть сторона A’C’, перенаправленная в другое положение).

Итак, во всех трех случаях оказалось, что

т. е., если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, но углы между ними не равны, то против большого угла лежит большая сторона.

88. Разберем обратный вопрос. Пусть построены ∆ABC и ∆A’B’C’ (чер. 95) так, что AB = A’B’, BC = B’C’, но AC > A’C’, т. е. два треугольника имеют по две равных стороны, но третьи стороны их не равны. Сравнить ∠B и ∠B’.
Воспользуемся тем же способом рассуждения, как в п. 86.

Пока мы можем об углах B и B’ сделать три предположения: 1) ∠B = ∠B’, 2) ∠B > ∠B’ и 3) ∠B ∠B’, которое и должно быть верно. Итак:

Если две стороны одного треугольника равны соответственно двум сторонам другого, но третьи стороны этих треугольников не равны, то против большей стороны лежит и больший угол.