Как решать задачи с вписанной окружностью в квадрат (7 видео)

Радиус окружности, вписанной в квадрат. Теория и решение

В этой статье популярно объяснено, как найти радиус окружности, вписанной в квадрат. Теоретический материал поможет вам разобраться во всех связанных с темой нюансах. Прочитав этот текст, вы с легкостью сможете решать подобные задачи в дальнейшем.

Содержание

Базовая теория
Радиус вписанной в квадрат окружности
Радиусы описанной и вписанной окружностей в квадрат
Окружность вписанная в квадрат
Окружность описанная около квадрата
Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.
Как решать задачи с вписанной окружностью в квадрат
📽️ Видео

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Базовая теория

Перед тем как перейти непосредственно к нахождению радиуса вписанной в квадрат окружности, стоит ознакомиться с некоторыми фундаментальными понятиями. Возможно, они могут показаться слишком простыми и очевидными, но они необходимы для понимания вопроса.

Квадрат — четырехугольник, все стороны которого равны между собой, а градусная мера всех углов составляет 90 градусов.

Окружность — двумерная замкнутая кривая, расположенная на определенном расстоянии от некоторой точки. Отрезок, один конец которого лежит в центре окружности, а второй — на любой ее поверхности, называется радиусом.

С терминами ознакомились, остался лишь главный вопрос. Нам нужно найти радиус окружности, вписанной в квадрат. Но что означает последняя фраза? Здесь тоже ничего сложного. Если все стороны некоторого многоугольника касаются кривой линии, то ее считают вписанной в этот многоугольник.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Радиус вписанной в квадрат окружности

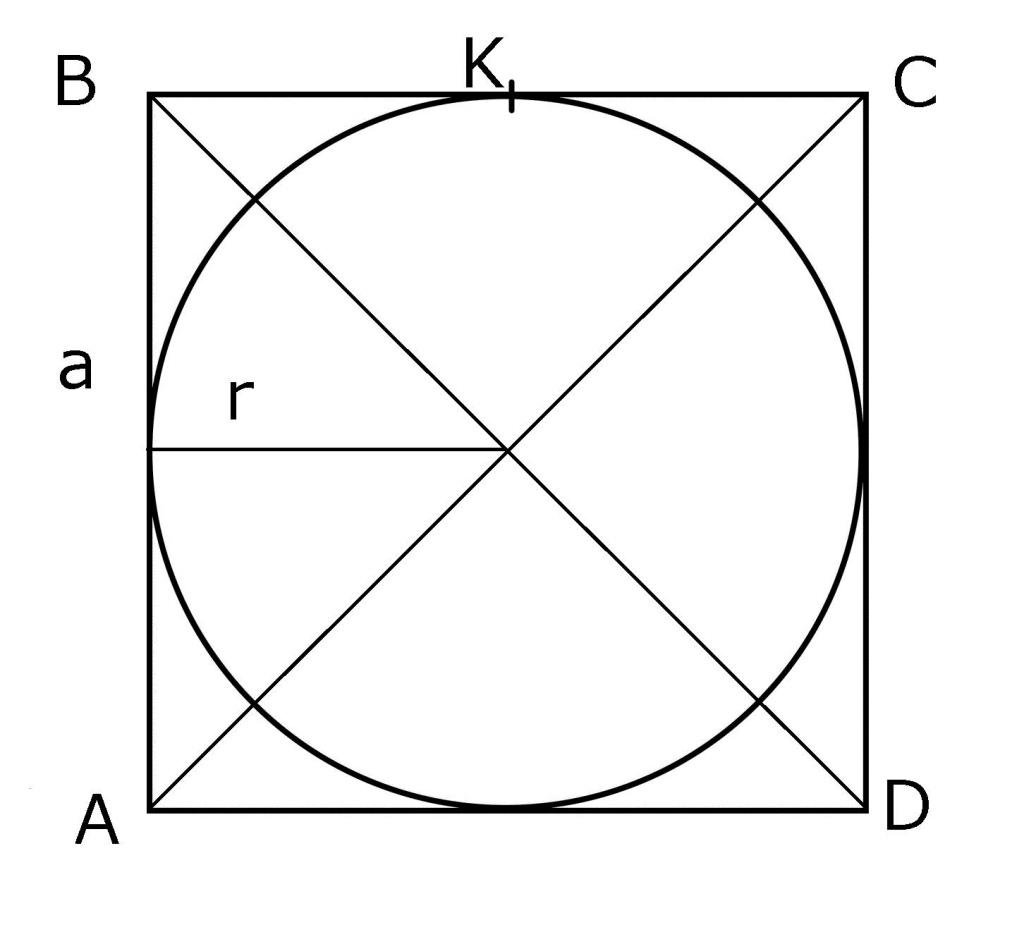
С теоретическим материалом закончили. Теперь необходимо разобраться в том, как применить его на практике. Воспользуемся для этого рисунком.

Радиус, очевидно, перпендикулярен AB. Это значит, что в то же время он параллелен AD и BC. Грубо говоря, можно «наложить» его на сторону квадрата, чтобы далее определить длину. Как видно, ей будет соответствовать отрезок BK.

Один из его концов r лежит в центре окружности, которая является точкой пересечения диагоналей. Последние по одному из своих свойств делят друг друга пополам. Используя теорему Пифагора, можно доказать, что они также делят и сторону фигуры на две одинаковых части.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Радиусы описанной и вписанной окружностей в квадрат

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Окружность вписанная в квадрат

Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:

все углы прямые, то есть, равны 90°;
все стороны, как и углы, равны;
диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.

При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.

Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:

Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Окружность описанная около квадрата

Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):

Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:

угол CDA=90°;
стороны AD=CD. Признак равнобедренного треугольника;
угол DAC равен ACD. Они равны по 45°.

Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:

Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.

треугольник ОСЕ – равнобедренный и прямоугольный;
ОЕ=ЕС=;
ОЕС=90°;
ЕОС=ОСЕ=45°;

Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Как решать задачи с вписанной окружностью в квадрат

Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Воспользуемся теоремой косинусов:

(здесь a и b — боковые стороны равнобедренного треугольника, c — основание.

Диаметр описанной окружности найдем по обобщенной теореме синусов:

Вместо того, чтобы искать основание треугольника, можно было найти угол при основании. Действительно, сумма углов при основании данного равнобедренного треугольника равна 60°. Эти углы равны, поэтому каждый из них равен 30°. Применяя обобщенную теорему синусов для боковой стороны и противолежащего ей угла, получаем: