Как решать треугольник авс

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные	Тупоугольные	Прямоугольные
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный.

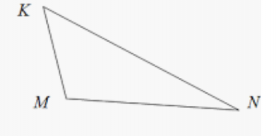Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Видео:ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:№1025. С помощью теорем синусов и косинусов решите треугольник ABC, если:Скачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:Геометрия ОГЭ задача Теорема синусовСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Видео:Решение задачи с применением теоремы синусовСкачать

Геометрия. 9 класс

Конспект
Элементами треугольника являются его стороны и углы.

Решить треугольник – это найти его неизвестные элементы, по каким-нибудь трём данным элементам.
Решим треугольник по двум сторонам и углу между ними.

Дано: a, b, ∠C
Найти: с, ∠А, ∠B
Зная две стороны и угол между ними, по теореме косинусов можно найти третью сторону треугольника.
Решение.
1) c 2 = a 2 + b 2 — 2ab cosC
с = √(a 2 + b 2 — 2ab cosC)
Запишем теорему косинуса для одной из известных сторон и выразим из этой формулы косинус противолежащего угла.
2) a 2 = b 2 + c 2 — 2bc cosA
cosA = (b 2 + c 2 — a 2 )/(2bc)
∠А находим по таблице или с помощью калькулятора.
Зная, что сумма углов треугольника равна 180°, можно вычислить третий угол.
3) ∠В = 180°- ∠А — ∠С.
Решение треугольника по стороне и двум прилежащим к ней углам.
Дано: с, ∠А, ∠B
Найти: a, b, ∠C
Решение.
Зная, что сумма углов треугольника равна 180°, вычислим третий угол.
1) ∠C = 180° — ∠А — ∠В.
Запишем теорему синусов данного треугольника и выразим неизвестные стороны треугольника.
2) b/sinB = c/sinC;
a/sinA = c/sinC
b = (c ∙ sinB)/sinC;
a = (c ∙ sinA)/sinC
Решение треугольника по трём сторонам.

Дано: a, b, с
Найти: ∠А, ∠B, ∠C
Решение.
Чтобы найти неизвестный угол треугольника, воспользуемся теоремой косинусов.
Вычислив косинус угла, сам угол находим по таблице или с помощью калькулятора.
1) a 2 = b 2 + c 2 — 2bc cosA
cosA = (b 2 + c 2 — a 2 )/(2bc)
∠А находим по таблице или с помощью калькулятора.
Так же, с помощью теоремы косинусов, найдём величину другого угла.
2) b 2 = a 2 + c 2 — 2ac cosB
cosB = (a 2 + c 2 — b 2 )/(2ac)
∠B находим по таблице или с помощью калькулятора.
Для вычисления третьего угла воспользуемся теоремой о сумме углов треугольника.
3) ∠А + ∠B + ∠C = 180°
∠C = 180° — ∠А — ∠B
С помощью тригонометрических формул можно определить высоту предмета, например, дерева.
Для этого отметим точку В на определённом расстоянии от точки Н, которая является основанием дерева, и измерим угол АВН. Из прямоугольного треугольника АВН, найдём высоту дерева.

AH = a tgα
Если основание дерева недоступно, то на прямой, проходящей через основание дерева – точку Н, отметим точки В и С на определённом расстоянии друг от друга. Измерим углы АВН и АСН. Решим треугольник АВС: найдём величину угла А и длину АВ.

В ∆ABC: ∠A = α — β,
AB/sin⁡C = BC/sin⁡A, тогда AB/sin⁡β = a/sin⁡(α — β).
AB = (a sin⁡β)/sin⁡(α — β).
Из прямоугольного треугольника АВН найдём высоту дерева – длину отрезка АН.
В ∆ABH : AH = AB ∙ sin⁡α.
Следовательно, AH = (a sin⁡β sin⁡α)/sin(α — β).
Предположим, что нам нужно найти расстояние от точки А до недоступного объекта С.
Выберем точку В и измерим длину отрезка АВ.
Измерим углы А и В, это можно сделать с помощью астролябии.

Зная сторону АВ треугольника АВС и значение двух углов, прилежащих к этой стороне, можно найти длину отрезка АС.
1) ∠C = 180° — α — β
sin⁡C = sin(180° — α — β) = sin⁡(α + β)
2) AC/sin⁡B = AB/sin⁡C;
AC = (AB sin⁡B)/sin⁡C = (c sin⁡β)/sin⁡(α + β)

📽️ Видео

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Найти площадь треугольника АВС. Задачи по рисункамСкачать

№1022. Площадь треугольника ABC равна 60 см2. Найдите сторону АВ, если АС= 15 см,Скачать

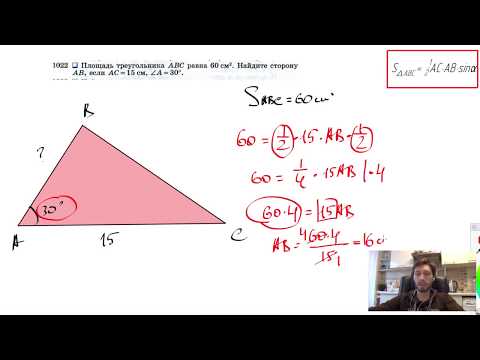
ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ПОДОБНЫЕ ТРЕУГОЛЬНИКИСкачать

9 класс, 15 урок, Решение треугольниковСкачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

9 класс, 13 урок, Теорема синусовСкачать

Задание 15 (В1) ОГЭ по математике ▶ №10 (Минутка ОГЭ)Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

№224. Найдите углы треугольника ABC, если ∠A:∠B:∠C= 2:3:4.Скачать

Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать