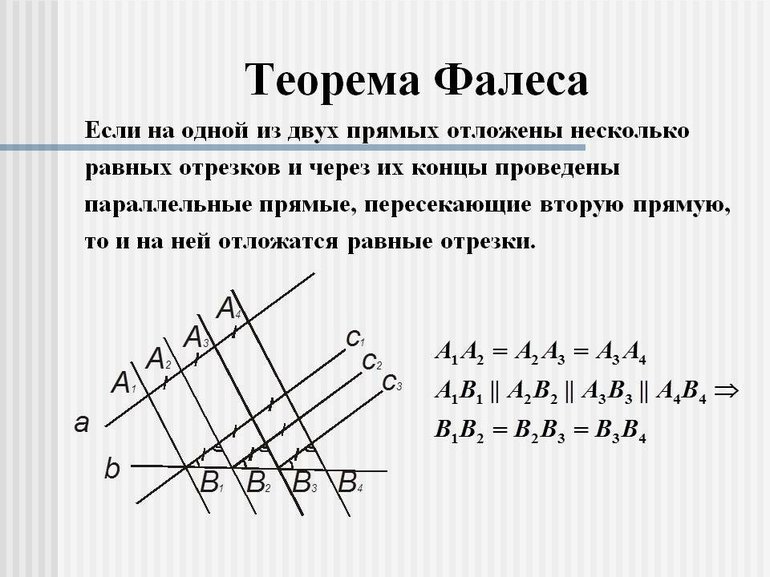
Как разделить отрезок при помощи окружностей (7 видео)

Делим отрезок на равные части

В школьные годы безумно полюбил геометрию на плоскости. Мечтал в будущем сделать яркие открытия и прослыть вторым Евклидом. Не помню уже в каком классе проходили метод деления отрезка на любое количество равных частей, однако он меня особо не вдохновил. Несмотря на универсальность. На рисунке а) наглядно показан. Показано, как разделить АВ на три равные части. Красными числами обозначил последовательность построений. На произвольном луче АС откладываем произвольные равные отрезки 1, 2, 3. Конец третьего отрезка соединяем с точкой В. Далее чертим параллельные линии 5 и 6. Они и разделят на три равные части искомый АВ.

А что я придумал в юношеские годы? Смотрим рисунок b). Ножку циркуля устанавливаем в точке А и радиусом АВ делаем две насечки 1 (наверху и внизу). Тем же радиусом, с центром в точке В, делаем две аналогичные насечки 2. Получим точки С и D. Третье действие: проводим прямую СВ и на ней находим середину — то есть точку К. Прямая КD пересекает наш отрезок АВ в точке N. И оказалось, что NB — это ровно треть всего АВ. Ну, а точка М легко строится циркулем. Задача красиво решена! Я тогда совершенно не был знаком с важными теоремами, которые сразу говорили бы о верности построений. Делал всё чисто эмпирически, рассматривая десятки разных вариантов. Думал, конечно, что родил величайшее открытие.

Содержание

ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ
Деление отрезка на равные части
Как разделить отрезок на равные части — формулы и способы
Два одинаковых значения
Получение четырех частей
Разложение при помощи циркуля
Теорема Фалеса
💡 Видео

Видео:Деление окружности на равные части с помощью циркуляСкачать

ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ

Знание основных геометрических построений дает возможность правильно и быстро чертить, выбирая для каждого случая наиболее рациональные приемы.

Видео:Деление отрезка на равные части, перпендикуляр к прямой.Урок 4.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление отрезка на равные части

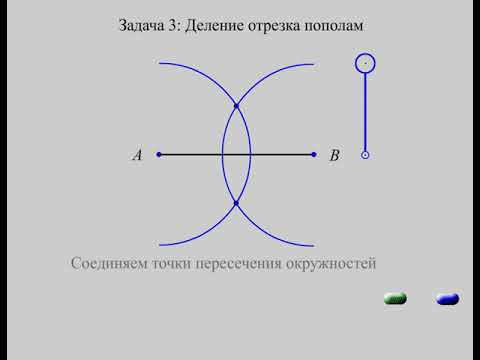
Разделить отрезок пополам можно при помощи циркуля, построив срединный перпендикуляр (рис. 14, а). Для этого берём радиус размером более половины длины отрезка и из его концов по обе стороны проводим дуги окружностей до их взаимного пересечения. Через точки пересечения дуг проводим срединный перпендикуляр.

Для деления на любое число равных частей используем теорему Фалеса: Если на одной стороне угла отложить равные между собой отрезки и через их концы провести параллельные прямые, то на другой стороне угла отложатся также равные между собой отрезки (рис. 14, б). Под произвольным углом к отрезку АВ проводим вспомогательный луч АС, на котором откладываем отрезок произвольной длины столько раз, на сколько частей следует разделить данный отрезок. Конец последнего отрезка соединяем с точкой В и через концы остальных отрезков проводим прямые, параллельные ВС.

Видео:Деление отрезка на 2,4,8 равных частей с помощью циркуля и линейкиСкачать

Как разделить отрезок на равные части — формулы и способы

Видео:1 2 2 деление окружности на 5 равных частейСкачать

Два одинаковых значения

Самый простой способ разделить на две равнозначные доли — воспользоваться линейкой. Необходимо отмерить общую длину от точки А до точки В и разделить это значение на два. Полученное число следует отметить на заданном интервале, совместив отметку 0 на линейке с точкой А.

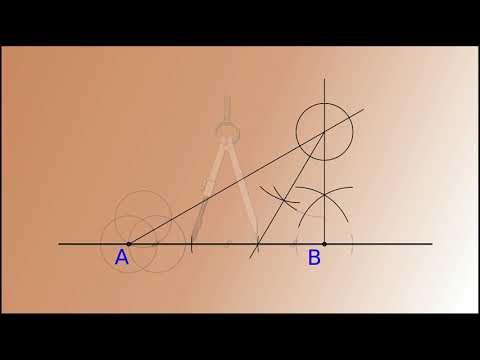
При делении на две идентичные доли можно воспользоваться циркулем. Для начала надо отмерить расстояние, которое будет несколько больше, чем предполагаемая половина исходной линии. Чертим две окружности, радиус которых мы определили циркулем. Одну окружность проводим из точки А, а другую — из В. Обе эти окружности между собой соединяются, образуя новые точки — С и D. Потом с помощью линейки и карандаша следует провести линию, соединяющую точки C и D. В том месте, где линия пересекает отрезок, образуется точка Е, которая является центром, а соответственно и делит его пополам.

Видео:Деление окружностей на равные частиСкачать

Получение четырех частей

В таком варианте деления можно в упрощённом виде воспользоваться линейкой. Здесь последовательно сначала отмеряется середина, то есть отрезок делится на две равные части, как указывалось выше, а затем каждый из осечённых секторов по отдельности разделяется пополам. Таким образом, получаются четыре равных отрезка.

Однако такой вариант оказывается удачным лишь на тех прямых, которые имеют целое числовое значение. Здесь следует воспользоваться циркулем.

Видео:Деление окружности на 3 частиСкачать

Разложение при помощи циркуля

Как и в первом описании, при помощи черчения двух окружностей заданный отрезок следует поделить пополам. Таким образом, на прямой образуется два отрезка — АЕ и ЕВ. Далее следует совершить аналогичные действия, но уже с двумя отрезками по отдельности. То есть, взяв отрезок АЕ, провести две окружности:

одну — из точки А;
вторую — из точки Е.

И снова в местах соединения этих двух дуг нужно провести прямую линию. Тот же самый алгоритм применяется и в отношении линии ЕВ. После проведённых манипуляций отрезок будет пересечён тремя перпендикулярными прямыми, а соответственно, разделён на четыре равные части.

Видео:ДЕЛЕНИЕ ОТРЕЗКА НА РАВНЫЕ ЧАСТИ 396 Атанасян 8 классСкачать

Теорема Фалеса

Если с делением на две или четыре равные части всё более или менее понятно, то деление отрезка на n равных частей вызывает определённые трудности. Здесь приходит на помощь формула параллельных прямых, описанная в теореме Фалеса.

Суть теоремы состоит в том, что при отложении одинаковых отрезков на одной прямой и проведении через концы этих отрезков параллельных прямых, пересекающих другую прямую, то и на второй прямой будут отложены равные между собой отрезки.

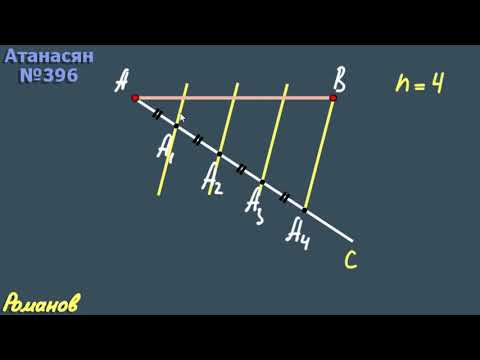
Например, на определённой прямой необходимо отмерить пять одинаковых отрезков. Для начала из точки А следует провести прямую линию, которая будет направлена в сторону противоположного конца отрезка (точки В) под острым углом относительно исходной прямой. Теперь при помощи циркуля на этой линии следует отложить пять равных отрезков. Из точки, отмерившей последний отсек, следует очертить линию в точку В. Затем провести прямые, параллельные той, которая проходит через точку В. Каждая линия должна проходить через отмеченные циркулем точки. При условии, что все линии будут строго параллельны друг другу, на исходной прямой будет отложено пять равных отрезков.

Зная, как производить деление на одинаковые части, можно, например, понять, как разделить треугольник на 4 равные части или более. По указанным вариантам деления на сегменты можно производить следующие действия: