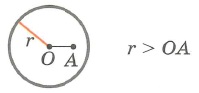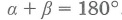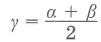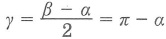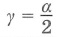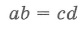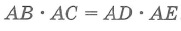Как расположена прямая относительно окружности если

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Взаимное расположение прямой и окружности

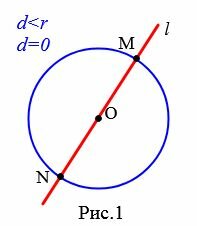
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.

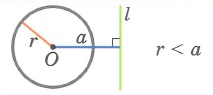
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.

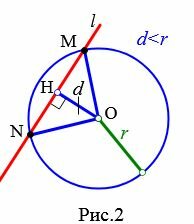Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

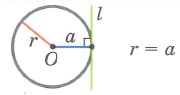
Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

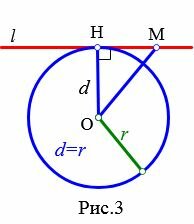Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.

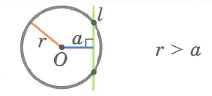
Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

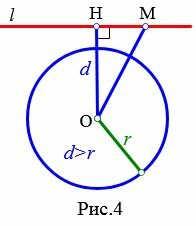Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Осевая и центральная симметрия

О чем эта статья:

Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:Уравнение окружности (1)Скачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности

Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.

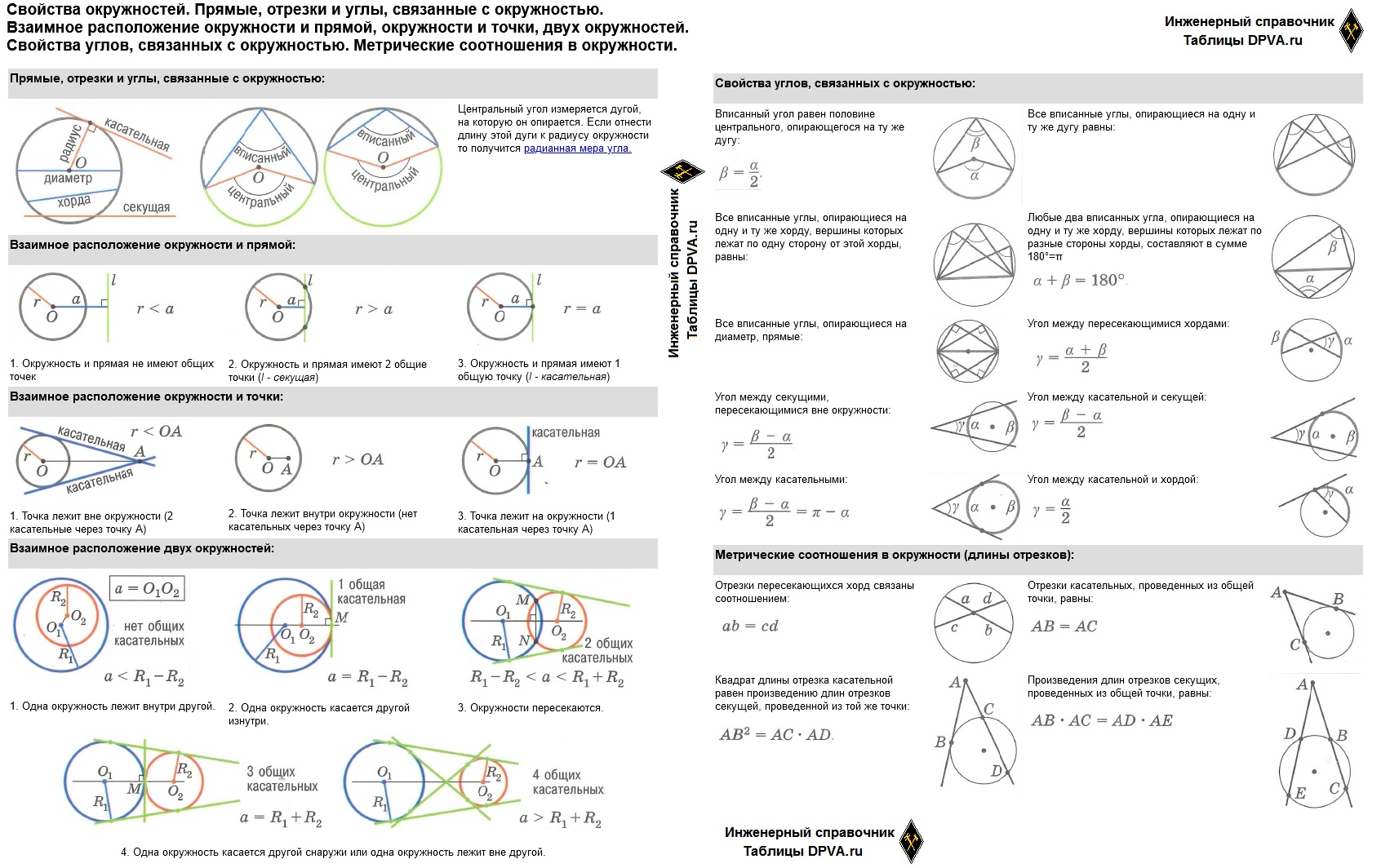
Прямые, отрезки и углы, связанные с окружностью:

Центральный угол измеряется дугой, на которую он опирается. Если отнести длину этой дуги к радиусу окружности то получится радианная мера угла.

Взаимное расположение окружности и прямой:

1. Окружность и прямая не имеют общих точек

2. Окружность и прямая имеют 2 общие точки (l — секущая)

3. Окружность и прямая имеют 1 общую точку (l — касательная)

Взаимное расположение окружности и точки:

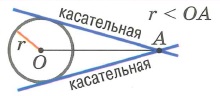
1. Точка лежит вне окружности (2 касательные через точку А)

2. Точка лежит внутри окружности (нет касательных через точку А)

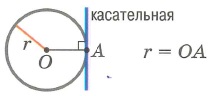
3. Точка лежит на окружности (1 касательная через точку А)

Взаимное расположение двух окружностей:

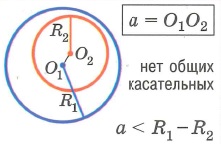
1. Одна окружность лежит внутри другой.

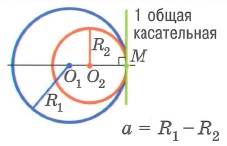
2. Одна окружность касается другой изнутри.

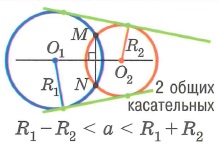
3. Окружности пересекаются.

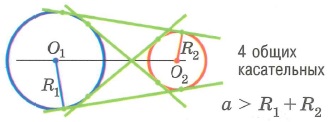
4. Одна окружность касается другой снаружи или одна окружность лежит вне другой.

Свойства углов, связанных с окружностью:

Вписанный угол равен половине центрального, опирающегося на ту же дугу:

Все вписанные углы, опирающиеся на одну и ту же дугу равны:Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны:

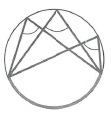
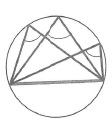
Любые два вписанных угла, опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°=π

Все вписанные углы, опирающиеся на диаметр, прямые:

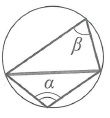
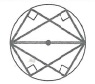
Угол между пересекающимися хордами:

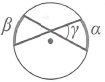
Угол между секущими, пересекающимися вне окружности:

Угол между касательной и секущей:

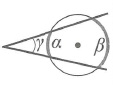
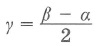
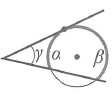
Угол между касательными:

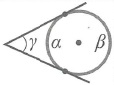
Угол между касательной и хордой:

Метрические соотношения в окружности (длины отрезков):

Отрезки пересекающихся хорд связаны соотношением:

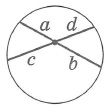
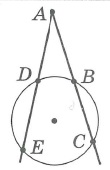
Отрезки касательных, проведенных из общей точки, равны:

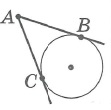
Квадрат длины отрезка касательной равен произведению длин отрезков секущей, проведенной из той же точки:

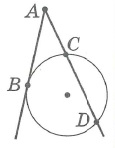
Произведения длин отрезков секущих, проведенных из общей точки, равны:

Консультации и техническая
поддержка сайта: Zavarka Team

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Как расположена прямая относительно окружности если

Вопрос по математике:

. Определить, как расположена прямая относительно окруж­ности (пересекает ли, касается или проходит вне её), если прямая и окружность заданы следующими уравнениями:
у = 2х – 3 и х 2 + у2 – 3 х + 2 у – 3 = 0
срочно надо решить

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

X^2+(2х-3)^2+2(2x-3)-3х-3=0
x^2+4х^2-12x+9+4x-12-3x-3=0
5х^2-11x-6=0,
D=(-11)^2-4•5•(-6)=121+120=241;D>0
Пересекаются в 2 точках

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:ТОП-5 ОШИБОК в математике | Математика | TutorOnlineСкачать

. Определить, как расположена прямая относительно окруж­ности (пересекает ли, касается или проходит вне её), если прямая и окружность заданы следующими уравнениями : у = 2х – 3 и х2 + у2 – 3х + 2у – 3?

Математика | 10 — 11 классы

. Определить, как расположена прямая относительно окруж­ности (пересекает ли, касается или проходит вне её), если прямая и окружность заданы следующими уравнениями : у = 2х – 3 и х2 + у2 – 3х + 2у – 3 = 0

срочно надо решить.

X ^ 2 + (2х — 3) ^ 2 + 2(2x — 3) — 3х — 3 = 0

x ^ 2 + 4х ^ 2 — 12x + 9 + 4x — 12 — 3x — 3 = 0

5х ^ 2 — 11x — 6 = 0,

D = ( — 11) ^ 2 — 4•5•( — 6) = 121 + 120 = 241 ; D&gt ; 0

Пересекаются в 2 точках.

Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

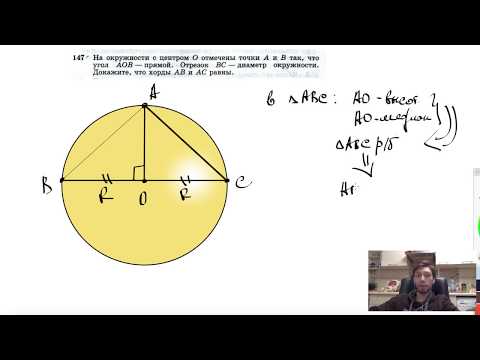
Постройте окружность радиусом 35 мм?

Постройте окружность радиусом 35 мм.

1) проведите прямую АВ, которая пересекает окружность.

2) проведите прямую СD, не пересекающую окружность.

3) проведите прямую прямую KL, которая касается окружности, т.

Е. имеет с окружностью единственную общую точку.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Начертите окружность и проведите три прямые её пересекающие?

Начертите окружность и проведите три прямые её пересекающие.

Как нужно провести прямую, чтобы расстояние между точками пересечение это прямой с окружностью было наибольшим?

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Начертите окружность диаметром 6 см и вне окружности отметьте точки C и D так , чтобы прямая CD не пересекалась с окружностью?

Начертите окружность диаметром 6 см и вне окружности отметьте точки C и D так , чтобы прямая CD не пересекалась с окружностью.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Начертите окружность и проведите три прямые её пересекающие?

Начертите окружность и проведите три прямые её пересекающие.

Как нужно провести прямую, чтобы расстояние между точками пересечение это прямой с окружностью было наибольшим?

Видео:Как Солнечная система движется по галактике?Скачать

Помогите пожалуйста?

Через точку В, отстаящую на 5 см от цента О окружности, проведена прямая, которая касается этой окружности в точке А.

Найдите расстояние от точки В до точки С.

В которой прямая Во пересекает окружность, учитывая, что АВ = 4 см.

Видео:Симметрия относительно точки. 6 классСкачать

Какая из прямых пересекает окружность?

Какая из прямых пересекает окружность?

Пересекаются ли прямые.

Видео:Стереометрия за МЕСЯЦ?! Решаем задачи с 0 до ЕГЭСкачать

Окружность касается другой окружности радиусом 12 см изнутри, и проходит через её центр?

Окружность касается другой окружности радиусом 12 см изнутри, и проходит через её центр.

Найти радиус меньшей окружности.

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Если расстояние от центра окружности до прямой меньше диаметра окружности то эта прямая и окружность пересекаются?

Если расстояние от центра окружности до прямой меньше диаметра окружности то эта прямая и окружность пересекаются.

Видео:Степень точки и радикальные оси | Олимпиадная математикаСкачать

Начертите круг с диаметром 4 см и вне окружности отметьте точку К от этой токи проведите к окружности прямую так чтобы она касалась окружности?

Начертите круг с диаметром 4 см и вне окружности отметьте точку К от этой токи проведите к окружности прямую так чтобы она касалась окружности.

Сколько таких прямых можно провести?

Видео:Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 1Скачать

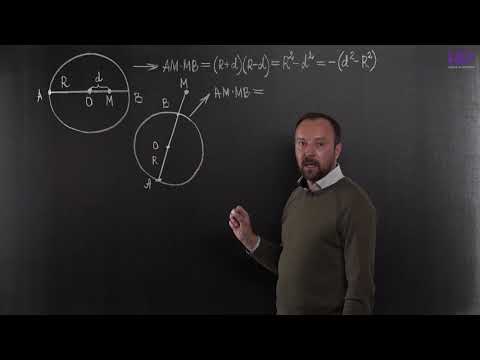
Как убедиться что если прямая не проходит через центр окружности то эта прямая не является осью симметрии для окружности?

Как убедиться что если прямая не проходит через центр окружности то эта прямая не является осью симметрии для окружности.

Если вам необходимо получить ответ на вопрос . Определить, как расположена прямая относительно окруж­ности (пересекает ли, касается или проходит вне её), если прямая и окружность заданы следующими уравнениями : у = 2х – 3 и х2 + у2 – 3х + 2у – 3?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.