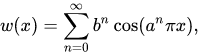Разделы: Математика
Круг и окружность – одни из самых древнейших геометрических фигур, философы древности придавали им большое значение. Круг – воплощение нескончаемого Времени и Пространства, символ всего сущего, Вселенной. “Из всех фигур прекраснейшая – круг”, – считал Пифагор.
Вокруг нас много круглых предметов. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезло все круглое! Казалось бы – пусть все будет квадратным. Разве нельзя прожить без круглых труб, а к квадратным колесам нельзя привыкнуть? Можно ли вообще представить жизнь человека без использования круга? Почему так много тел имеют круглую форму? Чтобы найти ответы на все эти вопросы, в первую очередь, необходимо рассмотреть историю возникновения этих понятий и дальнейшее их развитие.
История возникновения и развития геометрических понятий “круг” и “окружность”.
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, похожие на шар. Специальных названий для геометрических фигур, конечно, не было. Говорили: “такой же, как кокосовый орех” или “такой же, как соль” и т.д. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими фигурами.
Круглые тела еще в древности заинтересовали человека. В Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки. Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки, которые катились уже легче и с их помощью перетаскивали грузы. Так появилось первое колесо. К сожалению, неизвестен непосредственный изобретатель колеса.
Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму. Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность. Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания.
Математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой. В Древней Греции все разрозненные знания привели в систему, геометрия стала бурно развиваться как наука. Только в Древней Греции “окружность” и “круг” получили свои названия, почти все названия геометрических фигур греческого происхождения, как и само слово геометрия (“гео” – земля, а “метрио” – мерить). Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.
В Древней Греции многие свойства фигур, в том числе круга и окружности были сформулированы в виде теорем и доказаны. Наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах “Начала”. В течение многих веков “Начала” были единственной учебной книгой, по которой молодежь изучала геометрию. И даже сейчас, в наше время, учебники написаны под большим влиянием “Начал” Евклида.
Окружность и круг – это плоские фигуры . Мы живем в мире трех измерений. А в какое геометрическое тело превратятся окружность и круг, если попадут в пространство? Это сфера и шар. “Сфера” – произошло от греческого слова “сфайра”, в переводе – “мяч”. Кроме этого геометрия пространства рассматривает и другие круглые тела – это “цилиндр” (от греческого слова “кюлиндрос”, что означает “валик”, “каток”) и “конус” (от греческого слова “конос”, означающего “сосновая шишка”). Самым важным среди круглых тел был шар.
Итак, в Древней Греции круг и окружность считали венцом совершенства. “В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе”. Это свойство окружности стало толчком к возникновению колеса (Приложение 5). (Приложение 2).
Круг – “циркулус” – латинское слово, от него же и “циркуль”, без которого бы мы не построили круг. Циркуль и линейка – самые старые чертежные инструменты на Земле. (Приложение 3.)
Элементы окружности и круга (Приложение 2):
Радиус окружности – это отрезок, соединяющий центр окружности с любой ее точкой (по-латыни – спица колеса).
Диаметр окружности – это хорда, проходящая через центр окружности (с греческого – “поперечник”).
Хорда окружности – отрезок, соединяющий любые две точки на окружности (с греческого– “струна”).
Дуга окружности – это часть окружности, ограниченная двумя точками.
Часто в практических задачах нужно узнать длину окружности. А как измерить длину окружности, если сама окружность – кривая линия, а единица измерения длины – отрезок? Есть несколько способов измерения длины окружности (Приложение 1).
Однако эти способы непосредственного измерения длины окружности малоудобны и дают приближенные результаты. Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость: С:d ≈ 3,1.
Многие ученые – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности, его стали обозначать греческой буквой π-ο ервая буква греческого слова “периферия” – круг.
С:d = π, где С – длина окружности, d – длина диаметра, отсюда и формула длины окружности C = πd или C = 2πr.
Изучив исследования ученых математиков, мы провели следующие измерения и вычисления:
1. Вычисление числа пи : а) с помощью тонкой нити измерили длину окружности С некоторых предметов быта; б) чтобы точнее найти длину диметра d, приложили этот предмет к листу бумаги и обвели карандашом, вырезали, свернули пополам, линия сгиба – это диаметр, измерили его с помощью линейки; в) нашли отношение С:d, данные занесли в таблицу:
| Предметы | Длина окружности С | Диаметр d | Отношение С:d |
| Стакан | 22 см | 7 см | 3.1428 |
| Ведро | 82 см | 26 см | 3.1538 |
| Тарелка | 62 см | 19,5 см | 3,1794 |
| Кастрюля | 69 см | 22 см | 3.1363 |
| Бидон | 52 см | 16,5 см | 3,1515 |
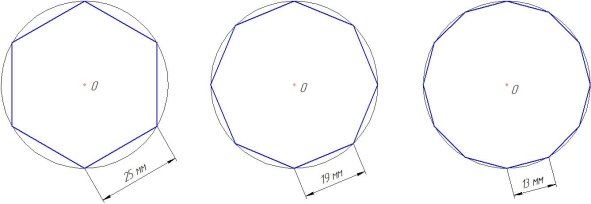
2. Границы значения числа пи: а) с помощью циркуля вписали круг в квадрат: если диаметр равен 1,то длина окружности равна π . Периметр квадрата со стороной 1 равен 4. Значит π меньше 4. (Приложение 6. Рис.1). б) в этот же круг вписали правильный шестиугольник: диаметр круга снова 1, длина окружности равна π . Сторона правильного шестиугольника равна радиусу, т.е.0,5,а периметр равен 6·0,5=3,значит π больше 3 (Приложение 6. Рис.2).
В результате мы убедились, что отношение длины окружности к ее диаметру (число π) есть число постоянное и 3 ‹ π ‹ 4 ,т.е. мы подтвердили исследования ученых – математиков.
Одна из загадок числа π состоит в том, что оно не может быть выражено какой – либо точной дробью. История числа π достойна восхищения, многие математики затратили на его вычисления не один десяток лет. Уточнялись нижняя и верхняя оценки числа и предпринимались неудачные попытки представить π в виде дроби и, таким образом, окончательно найти его значение (Приложение 4). Пока рекорд принадлежит японскому математику, в 2004 году – Ясума Канада из Токио рассчитал число π на компьютере до 1,24 триллиона знаков.
π -3,141 592 653 589 793 238 462 643 383279 502 884197 169 399 375 105 ….
Зачем нужно π, да еще с такой точностью? Число π чрезвычайно важно для ученых и инженеров. Все, что круглое и все, что движется по кругу (как колеса или планеты), содержит π. Без π люди не могли создать автомобили, понять движение планет или сосчитать сколько гороха поместится в консервную банку. Но загадка таинственного числа не разрешена вплоть до сегодняшнего дня, и, по-прежнему, волнует ученых. В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Все это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.
Изучив литературу и проделав собственные измерительные исследования с окружностью и кругом, мы пришли к следующим выводам: окружность и круг – это удивительно гармоничные фигуры. Окружность – единственная кривая, которая может “скользить сама по себе”, вращаясь вокруг центра. Это свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль, и почему колеса делают круглыми, а не квадратными или треугольными.
Круг в окружающей жизни.
Исследуя вопрос о роли круга в окружающей жизни, мы провели анкетирование обучающихся 5-9 классов и педагогов МО ШИСП (всего 90 человек):
- Какие круглые тела вы встречаете в окружающей жизни?
- Какое значение имеет круг в других науках?
- Какие практические задачи повседневной жизни решаются, используя знания о круге и окружности?
- Как вы считаете, почему встречается так много круглых тел в природе?
Ответы на первый вопрос представлены в презентации.
Из ответов учителей – предметников на второй вопрос анкеты мы поняли, что круг имеет большое значение не только в математике, но и в других науках:
| Предмет | Использование |
| Физика и астрономия | Движение небесных тел происходит по круговым орбитам. Зодиакальный круг, астрономический круг. Круг с точкой в центре символизирует солнце. |
| География | Меридианы и параллели, определяющие положение тела на земном шаре, экватор. Круговые процессы-циклы: круговорот воды и веществ в природе. Смена времен года, смена дня и ночи. |
| Химия | Строение атома: ядро круглое, электроны вращаются вокруг ядра по круговым орбитам. |
| Биология | У всех клеток есть круглое ядро. Круглую форму имеют клетки крови, цилиндрическую – клетки многих желез. Стебли растений и стволы деревьев, кости человека – круглые. Кровообращение идет по кругу. Овощи и фрукты имеют шарообразную или конусовидную форму. Цикличность развития живых существ. |
| Русский язык | В русском языке слово “круглый” означает высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”. От слова круг образовано множество различных слов: круглый, кругленький, округлить, округлиться, округлый, кругом, вокруг, окружать, кружить и многое другое. Округлые формы, круглое лицо, кругленькие щеки, круглый год, голова идет кругом, ходить по кругу – часто употребляемые выражения. |
| История и обществознание | “Круглый стол” – конференции, кругооборот капитала, круг семьи , колесо истории, “большой и малый круг истории” – исторические циклы. |
Проанализировав ответы на третий вопрос анкеты, мы поняли, что знания о круге и окружности позволяют человеку решать многие практические задачи в повседневной жизни: разбить клумбу или фонтан, сделать круглую крышу, окно или крышку, сшить головной убор, связать салфетку, сделать елочную игрушку, сделать выкройку платья или юбки, нарисовать узор и т.п.
Таким образом, круг в жизни человека имеет очень важную роль, и в жизни без круглых предметов обойтись невозможно.
Не все, кого мы анкетировали, смогли дать ответ на четвертый вопрос.
Здесь мы помещаем самые интересные и распространенные ответы:
- Только круглые предметы могут катиться, и поэтому их легче перемещать.
- Потому что, куда бы мы не пошли, мы возвращаемся, т.е. идем по кругу.
- У круга нет углов, и поэтому он удобен в применении, например, круглые монеты не могут порвать карман, о них не уколешься, не порежешься.
- Мячик не может быть квадратным, он не будет отпрыгивать.
- Посуду делали из глины, и округлую форму было легче придать, чем квадратную. Круглую посуду легче мыть, не надо выскребать из углов, в ней удобней размешивать.
- Легче изготовить круглое, чем угловатое. Многие технические процессы легче для тел вращения.
- На круглую форму идет меньше материала, чем на квадратную.
- Круглая крышка люка никогда не провалится, в отличие от квадратной.
- Все банки и крышки круглой формы, т.к. каждая точка окружности является точкой концентрации напряжения, и ее легко открыть, у прямоугольной формы такими точками являются только углы.
- Потому ,что солнце круглое, а без солнца мы не могли бы существовать.
- Круглая форма универсальна в природе.
Почему же на самом деле встречается так много круглых тел? Мы обратились к научным источникам. На этот вопрос можно ответить, рассмотрев мыльный пузырь, т.к. он идеально круглой формы. Силы поверхностного натяжения не дают лопнуть мыльному пузырю и стремятся придать мыльному пузырю максимально компактную форму. Самая компактная форма в природе – это шар. При шарообразной форме воздух внутри пузыря равномерно давит на все участки его внутренней стенки.
В небе много круглых объектов: Солнце, Луна, планеты, звезды. Почему не быть хотя бы одной некруглой планете? Ну, пусть одна, будет кубическая или пирамидальная. Но это невозможно? Есть сила, которая во всей Вселенной превращает миры в гладкие шары. Эта сила – сила тяготения. Каждый предмет имеет свою гравитацию, притягивает к себе другие тела, а также и свои части. Чем больше тело, тем сила тяжести увеличивается. Земля наша огромная, поэтому она имеет свою большую силу тяжести, которая заставляет притягиваться все к ее центру, а тело преобразовываться в шар. Если бы в силу каких-то причин удалось изменить нашу планету и придать ей иную форму, не шара, то спустя некоторое время она снова стала бы шарообразной. С телами на земле это не происходит, потому что их сила очень маленькая и сила тяжести Земли препятствует этому. Но если взять, например, каплю воды и запустить в космос, она сразу же преобразуется в шар. Именно жидкость способна преобразовываться в шарообразную форму. Земля состоит в основном из магмы (жидкости) поэтому и имеет форму шара.
Таким образом, мы пришли к выводам, что сама природа выбирает эту удобную и компактную форму – шара.
Кроме того, окружность и круг в виде сферы и шара – самая распространенная форма во Вселенной.
Круг и окружность – это еще и траектория движения Земли вокруг Солнца, это перемещение звезд на небе, это цикличность всех процессов, происходящих в мире. Если бы необходимо было бы выбрать форму, наиболее точно передающую устройство мира, то это были бы окружность и круг.
Изучив научную литературу, мы сделали вывод, что с незапамятных времен люди используют в своей жизни круг.
1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).
2. Мы не можем представить свою жизнь без машин: автобус, трактор, велосипед, швейная, стиральная и пишущая машинки, самолет, вездеход, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес. Зубчатые колеса спрятаны внутри многих машин, одно колесо заставляет вращаться другое, колеса с желобком –блоки, помогающие поднимать тяжелые грузы. Машины из века в век совершенствовались и совершенствуются, но неизменным остается использование в них колеса, как основной детали.
3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений, у многих народов символизирующая динамизм и бесконечное движение в противовес квадратам домов, участкам земли и городам оседлых и зерносеющих народов. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир (Приложение 7).
Есть в математике задачи, которые до сих пор не разрешены, например, знаменитая задача о “квадратуре круга” – о построении квадрата, равновеликого данному кругу и т.д.
5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль (Приложение 8).
6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство, бесконечность, отсутствие начала и конца, верха и низа, цикличность, повторяемость, завершенность. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду; небесные миры, землю и преисподнюю; фазы луны; восходящее, полуденное и заходящее солнце. Многие народы используют круг в религии, как символ связи земного с космосом.
В последнее время в разных местах земного шара стали появляться круги на полях, которые создают посланцы иных миров, желая о чем-то предупредить землян. (Приложение 9).
7. В энциклопедии мы нашли еще много понятий связанных с кругом: кругловязальная машина, круглочулочный автомат, круглогубцы, кругломер, “круговая система” в спорте, кругозор, круг друзей, круг общения, спасательный круг, святой круг, спиритический круг, круговая оборона, круговая порука, круглосуточная аптека, круги вокруг глаз.
- Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
- Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.
- Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.
- Круг – символ цикличности, повторяемости. Все движется по кругу.
- Круг дает ощущение взаимосвязи с Космосом.
- Сама природа выбирает эту удобную и компактную форму как шар и круг.
- История возникновения и развития геометрических понятий “круг” и “окружность”.
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Оставьте свой комментарий
- Подарочные сертификаты
- Прямые, кривые и очень изломанные. Краткая история линии от «Начал» Евклида до фракталов начала XX века
- Узоры древности
- Греция: длина без ширины
- Читайте также
- Вторжение иррационального
- Координаты и разрывы
- В действительности нечто похожее на уравнение встречается у Архимеда и Аполлония Пергского — это так называемые симптомы конических сечений.
- Длина кривой
- Мы расставляем n точек на равном расстоянии вдоль кривой, после чего замеряем длину прямых отрезков между этими точками (это мы делать умеем). Интуитивно возникает подозрение, что с увеличением числа n мы будем приближаться к значению настоящей длины — прирост суммы будет всё меньше, сверху он ограничен настоящей длинной кривой.
- Гладкость
- Может быть интересно
- Бесконечность в глубине отрезка
- В 1903 году Уильям Фогг Осгуд рассмотрел кривую, которая, являясь жордановой кривой, заполняет собой квадрат и в некоторых своих частях (более строго — порциях) имеет ненулевую площадь.
- Заполнить плоскость
- Здесь нужно сделать важное уточнение — отображение с отрезка на квадрат, построенное Пеано, не взаимно-однозначно: не существует кривых Пеано, в которых каждая точка квадрата проходится только единожды — везде при этом построении возникают кратные точки.
- Фракталы
- Читайте также
- Интересно, что тотально (то есть на любой порции) неспрямляемая кривая очень плохо помещается в ту же концепцию кривой как траектории движения. Точка, движущаяся по такой траектории, очевидно движется не по законам классической механики.
- 🔥 Видео
Видео:Что такое круг окружность радиусСкачать

История возникновения и развития геометрических понятий “круг” и “окружность”.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
История возникновения и развития геометрических понятий “круг” и “окружность”. Презентацию подготовила ученица 5 класса МОУ СОШ п. Мирный Вершинина Мария Учитель математики: Жумашева Айганым Айдабаевна
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, похожие на шар. Специальных названий для геометрических фигур, конечно, не было. Говорили: “такой же, как кокосовый орех” или “такой же, как соль” и т.д. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими фигурами.
Круглые тела еще в древности заинтересовали человека. В Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки.
Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки, которые катились уже легче и с их помощью перетаскивали грузы. Так появилось первое колесо. К сожалению, неизвестен непосредственный изобретатель колеса.
Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму. Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность. Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры.
Математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой. В Древней Греции все разрозненные знания привели в систему, геометрия стала бурно развиваться как наука. Только в Древней Греции “окружность” и “круг” получили свои названия, почти все названия геометрических фигур греческого происхождения, как и само слово геометрия (“гео” – земля, а “метрио” – мерить). Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.
В Древней Греции многие свойства фигур, в том числе круга и окружности были сформулированы в виде теорем и доказаны. Наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах “Начала”.
Окружность и круг – это плоские фигуры. Мы живем в мире трех измерений. А в какое геометрическое тело превратятся окружность и круг, если попадут в пространство? Это сфера и шар. “Сфера” – произошло от греческого слова “сфайра”, в переводе – “мяч”. Кроме этого геометрия пространства рассматривает и другие круглые тела – это “цилиндр” и “конус”. Самым важным среди круглых тел был шар.
Итак, в Древней Греции круг и окружность считали венцом совершенства. “В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе”. Это свойство окружности стало толчком к возникновению колеса.
Спасибо за внимание!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 943 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 701 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 331 человек из 72 регионов
Ищем педагогов в команду «Инфоурок»
- Жумашева Айганым АйдабаевнаНаписать 6504 24.06.2017
Номер материала: ДБ-578341
- 24.06.2017 1187
- 24.06.2017 2324
- 24.06.2017 2490
- 24.06.2017 2602
- 24.06.2017 976
- 24.06.2017 407
- 24.06.2017 137
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет
Время чтения: 3 минуты
Ретроспектива культовой сказки «Вечера на Хуторе близ Диканьки»
Время чтения: 5 минут
Стартовал региональный этап Всероссийской олимпиады школьников
Время чтения: 2 минуты
В Подмосковье вводят систему голосования оценки качества школьных столовых
Время чтения: 1 минута
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:7 класс, 21 урок, ОкружностьСкачать

Прямые, кривые и очень изломанные. Краткая история линии от «Начал» Евклида до фракталов начала XX века
Что такое линия? Чем отличаются разные кривые друг от друга? Эти вопросы математики задают себе уже 2500 лет, и путь к ответам на них не лишен драматизма — открытие иррациональных длин отрезков было, по легенде, трагедией для мировоззрения пифагорейцев, а открытие заполняющих плоскость кривых Пеано в начале ХХ столетия заставило ученых пересмотреть свои представления о непрерывности и размерности пространства. Математик и художник Давид Кац — об истории понятия «кривая» в математике Античности и Средневековья и математическом анализе Нового времени.
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Узоры древности
Интерес человека к прямым и искривленным линиям можно отследить с древнейших времен. Самые разные кривые мы видим в геометрических узорах на керамике и в архитектуре. Кроме достаточно простых узоров, составленных из прямых линий, часто можно встретить и что-то более сложное: спирали, волнистые линии и другие.

Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца. Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку.
Видео:Построить описанную окружность (Задача 1)Скачать

Греция: длина без ширины
Древние греки подошли к вопросу более строго. В «Началах» Евклида возникают определения (впрочем, зачастую носящие скорее описательный характер — на них, например, не ссылаются далее) линии, прямой линии, точки. Выглядят они, мягко говоря, несовременно:
Определение 1.1. Точка — это то, часть чего есть ничто.
Определение 1.2. Линия — это длина без ширины.
Определение 1.3. Концы линий — это точки.
Определение 1.4. Прямая линия лежит равномерно по отношению к точкам на ней. (Или: Прямая линия есть та, которая равно лежит на всех своих точках.)
Первое из этих определений можно при желании трактовать в духе теории множеств, третье, по-видимому, намекает, что линии у нас априори конечные. Второе можно трактовать описательно, что касается четвертого, то мнения сильно расходятся.
Несколько иная, хотя местами и похожая ситуация возникает в труде, традиционно приписываемом Герону, — «Определение понятий геометрии» (но в статье W. R. Knorr, ‘Arithmêtikê stoicheiôsis’: on Diophantus and Hero of Alexandria, Historia Math. 20 (2) (1993), 180–192 приводятся аргументы в пользу принадлежности его Диофанту):
Прямая линия — это линия, которая одинакова по отношению ко всем точкам на ней, лежит прямо и максимально натянута между своими концами.
Последнее определение довольно явно отсылает нас к кратчайшему расстоянию между двумя точками.
Читайте также
В наиболее известных трудах древних греков рассматриваются главным образом прямые линии. Хотя в некоторых трудах встречаются и иные известные им линии.
Аполлоний Пергский, один из трех великих геометров Античности (вместе с Евклидом и Архимедом), занимался коническими сечениями. Об их существовании знали и до него, однако именно он дал им названия, закрепившиеся в науке, — эллипс, гипербола, парабола.
Приведем и несколько других примеров, известных грекам.
Знаменитая архимедова спираль:
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Вторжение иррационального
Кстати, даже в случае отрезков и прямых линий уже у греков возникли определенные проблемы. Давайте пройдем этот путь вместе с ними. Возьмем квадрат со стороной 1. Нетрудно посчитать, используя теорему Пифагора, что его диагональ будет равна корню из двух. Мы моментально попадаем в неловкую ситуацию: корень из двух (как мы знаем сейчас) — число иррациональное , а это значит, что если вы уменьшите сторону квадрата в целое число раз, то из полученных отрезков не сможете получить его диагональ: будет либо чуть больше, либо чуть меньше. Можно было бы сослаться здесь на неточность вычислений или измерений, но пифагорейцы получили этот результат вовсе не на практике, а из теоретических соображений. Доказательство их выглядело следующим образом:
Пусть есть квадрат ABCD. Предположим, существует такой отрезок, который укладывается m раз на диагонали AC и n раз на стороне AB. Тогда AC : AB = m : n. Без ограничения общности можно считать, что хотя бы одно из двух этих чисел нечетно (если это не так и оба четны, то пусть m = 2 l m1, а n = 2 k n1, где m1 и n1 нечетны; поделим m и n на минимальное из чисел 2 l и 2 k , получим два числа m′ и n′ такие, что AC : AB = m′ : n′ и по крайней мере одно из них нечетно. В дальнейшем вместо m′ и n′ будем писать m и n и считать, что одно из этих чисел нечетно).
Если построить квадрат со стороной AC (скажем, ACEF), то площадь этого квадрата будет относиться к площади квадрата ABCD как m 2 к n 2 .
Согласно теореме Пифагора, площадь квадрата со стороной AC вдвое больше, чем площадь квадрата ABCD. Таким образом, m 2 = 2n 2 . Значит, m — четное число. Пусть оно равно 2N. Тогда m 2 = 4N 2 . Так как 4N 2 = 2n 2 , n 2 = 2N 2 . Значит, n — тоже четное. Это противоречит предположению о том, что одно из чисел m и n нечетно.
Для пифагорейцев это была печальная новость — в рамках арифметики им такие числа не встречались, поэтому казалось, что и в целом вычисления с длинами оказывались под угрозой.
Интересно, что позже, в рукописи «Выпрямляющий кривое» (в рамках нашей статьи это предельно интригующее название — чуть позже станет понятно почему) некоего Альфонсо, предположительно, крещеного еврея, жившего в Испании между XIII и XV веками, к несоразмерности длин отношение уже гораздо более доброжелательное:
«Следует знать, что от ученых не скрыто то, как поступают люди, которые обвивают прямыми тонкими нитями из шелка, или льна, или другого материала скрепленный круг и измеряют его окружность прямой линией. Однако следует знать, будет ли на самом деле так, как это воспринимается чувством, которое обладает приблизительностью, ибо чувство недостаточно для этого при той приблизительности, которая имеется в нем. Ведь всякие две линии, не равные друг другу, можно разрезать на очень маленькие части так, что чувством будут их воспринимать как равноценные. Вместе с тем возможно, что эти величины несоизмеримы и что видов иррациональной меры бесконечное количество, как это доказано в 10-й книге Евклида».
Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Координаты и разрывы
Значительное развитие в понимании кривых линий произошло с переходом от геометрического описания к алгебраическому — в частности, к описанию кривых через уравнения.
В действительности нечто похожее на уравнение встречается у Архимеда и Аполлония Пергского — это так называемые симптомы конических сечений.
Затем координаты (в виде заимствованных из географии понятий долготы и широты) встречаются у Николая Орезмского во второй половине XIV столетия. В XVI веке Виет начал использовать символы для записи уравнений. И, наконец, Рене Декарт (синхронно с ним — Пьер де Ферма) развил идеи, совмещающие символьную запись уравнений и систему координат. Его труд пользовался огромной популярностью и быстро получил широкое распространение и существенное развитие. В системе координат появились отрицательные значения, саму сетку координат научились строить косоугольной.
Этот подход, хотя и ограниченно, применял Ньютон. Впоследствии Кеплер для представления траекторий движения планет активно использовал конические сечения в координатах, геометрически описанные еще греками.
Предыдущие шаги сформировали понятие алгебраической кривой — множества точек, чьи координаты связаны уравнением кривой.
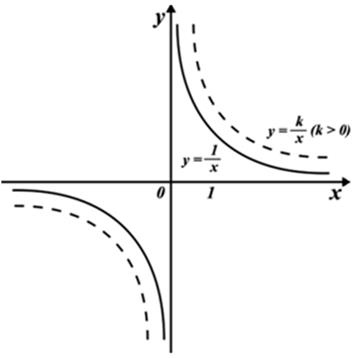
Интересно, что уже на этом, алгебраическом уровне возникают кривые с любопытными особенностями. Возьмем, например, известную многим со школы гиперболу — график функции 1/x. Его можно построить по точкам, но несложно сообразить, что уравнение y = 1/x имеет решение для любого x, кроме одного: x = 0 (на ноль делить нельзя). Это сказывается и на графике:
Что происходит в окрестности нуля? Нетрудно ответить. Давайте подойдем к нему справа. Когда мы подставляем в качестве x в выражение 1/x целое число больше 1, мы получаем дробь. Чем больше число, тем меньше получается дробь — этим и объясняется то, что график идет всё ниже и ниже по мере продвижения вправо. Подставляем х = 100, получаем у = 1/100, подставляет 1000000, получаем 1/1000000. Когда мы подставим в выражение единицу, на выходе получим единицу. Теперь пойдем в обратную сторону, ближе к нулю. Когда мы подставляем в выражение для y ½, она попадает в нижнюю часть дроби. Как мы помним, когда мы делим что-то на дробь, нам нужно умножить на перевернутую эту дробь. Значит, мы получим 2. Очевидно, чем ближе мы к нулю, тем сильнее уходим вверх — подставив 1/1000000, мы получим у = 1000000. Похожая ситуация при подходе слева, но с отрицательным знаком.
То, что происходит в нуле, называется разрывом (по виду графика хорошо понятно почему). В анализе принято классифицировать точки разрыва особым образом. То, что мы сейчас видели, называется точкой разрыва второго рода, поскольку односторонние пределы с двух сторон бесконечны (достаточно того, что один из них бесконечен). Если же односторонние пределы в точке разрыва конечны, то такая точка называется точкой разрыва первого рода.
Видео:Длина окружности. Математика 6 класс.Скачать

Длина кривой
С самого начала людям хотелось описывать не только сами объекты, но и их свойства. И раз уж мы говорим о «длине, лишенной ширины», хотелось бы уметь эту длину считать. Мы хорошо умеем считать длины прямых отрезков при помощи линейки, которая позволяет нам определять расстояние между двумя точками, но когда дело касается кривых линий, нам нужен иной метод.
Мы расставляем n точек на равном расстоянии вдоль кривой, после чего замеряем длину прямых отрезков между этими точками (это мы делать умеем). Интуитивно возникает подозрение, что с увеличением числа n мы будем приближаться к значению настоящей длины — прирост суммы будет всё меньше, сверху он ограничен настоящей длинной кривой.
Для простых примеров — скажем, окружностей, синусоид, парабол — этот подход отлично работает. Примеры, в которых он дает сбой, мы рассмотрим далее.
Видео:Как Эратосфен измерил диаметр Земли?Скачать

Гладкость
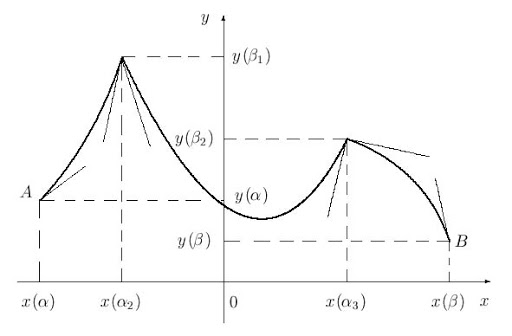
Еще одним свойством, характеризующим кривые, является гладкость. Хотя смысл слова интуитивно понятен, задать ее математически не совсем элементарно. Мы хотим, чтобы у кривой не было углов, заострений, клювов и т. п.
Хороший пример гладкой кривой — синусоида:
А вот пример негладкой кривой:
Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.
В курсе начал анализа доказывается, что такая касательная неразрывно связана с производной функции, график которой образует нашу кривую: более конкретно — тангенс угла наклона касательной (по отношению к положительному направлению оси Ox) равен значению производной функции в точке касания.
Эта связь позволяет нам четко определить гладкость функции. Чтобы функция называлась гладкой (и, следовательно, ее график был гладкой кривой), необходимо, чтобы, во-первых, эта функция была непрерывной, во-вторых, ее производная должна существовать и быть непрерывной .
Может быть интересно
Кажется, что гладкость — довольно естественное требование к кривой. Это ощущение привело к тому, что в 1806 году Андре-Мари Ампер выдвинул гипотезу о том, что любая функция всюду, за исключением отдельных, «исключительных и изолированных» точек, имеет производную в этих точках.
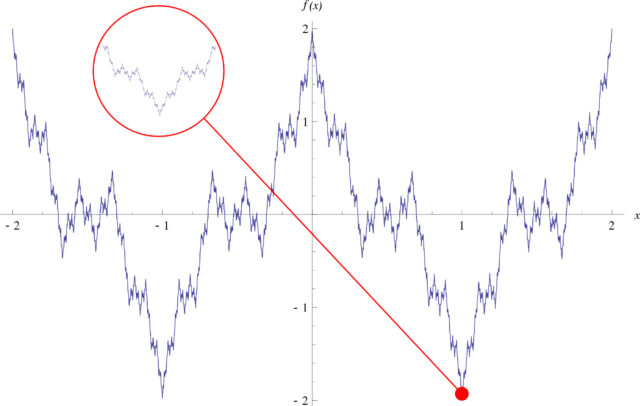
Позднее гипотеза была разрушена. Первый контрпример следует атрибутировать, по-видимому, Бернхарду Риману. Более простой и широко известный контрпример был построен Ван дер Варденом позднее, в 1930 году. Но наибольшей известностью пользуется функция Вейерштрасса, выраженная формулой:
здесь a — любое нечетное число кроме единицы, b — число от нуля до единицы, а большая греческая cигма обозначает суммирование. Функция оказывается непрерывной для всех вещественных х, но при ряде условий на a и b очень негладкой:
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Бесконечность в глубине отрезка
Совсем другой подход к кривым предложил великий французский математик Мари Энмон Камиль Жордан. Что если мы возьмем все точки отрезка и с помощью некоторого отображения перенесем их в пространство? Представьте, что наш отрезок сделан из проволоки, которую можно гнуть, вытягивать и сжимать. С помощью сжатия и вытягивания мы можем добиться изменения длины нашего отрезка, а с помощью сгибания — изменения его формы. Если же строго, то жордановой дугой называется образ непрерывного вложения отрезка в пространство: то есть разные точки отрезка обязательно перейдут в разные точки кривой. Можно представить, что отрезок у нас — временной, скажем, от начала работы секундомера до конца его работы. Тогда каждую секунду мы переводим в какое-то положение точки.
Жордановой замкнутой кривой называют образ непрерывного вложения окружности в пространство (из накладываемых требований следует, что окружность обязательно перейдет в некоторую замкнутую линию).
И хотя концепт жордановой кривой кажется достаточно простым, с его помощью можно получить весьма парадоксальные результаты.
В 1903 году Уильям Фогг Осгуд рассмотрел кривую, которая, являясь жордановой кривой, заполняет собой квадрат и в некоторых своих частях (более строго — порциях) имеет ненулевую площадь.
Впоследствии Кнопп построил жорданову кривую, обладающую ненулевой площадью вдоль всей кривой. Этот результат достигается за счет очень узких вырезаемых «клиньев», узость которых приводит к тому, что вычитаемая из площади треугольника площадь падает экспоненциально.
Кстати, вот здесь можно построить ее самостоятельно.
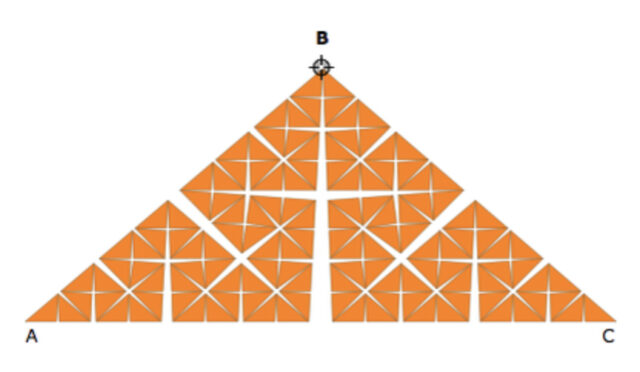
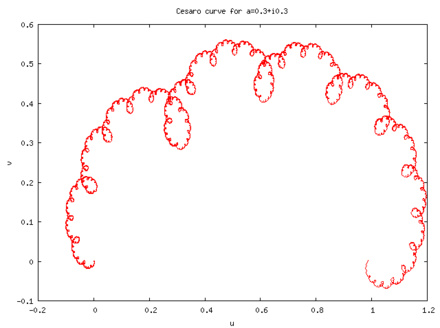
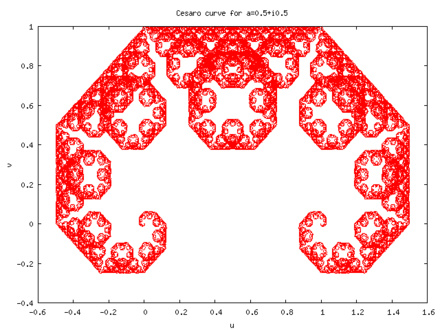
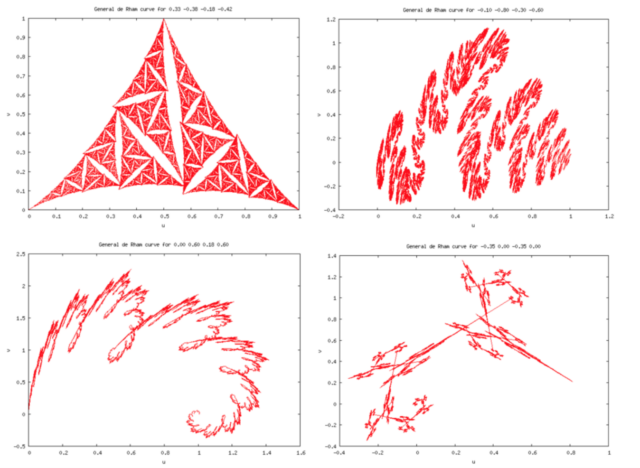
Примеров на эту тему много. Здесь мы упомянем полученные аффинными преобразованиями кривые де Рама:
кривую Коха — Пеано
и еще несколько кривых де Рама:
Видео:Окружность и все, что нужно про нее знать. ТеорияСкачать

Заполнить плоскость
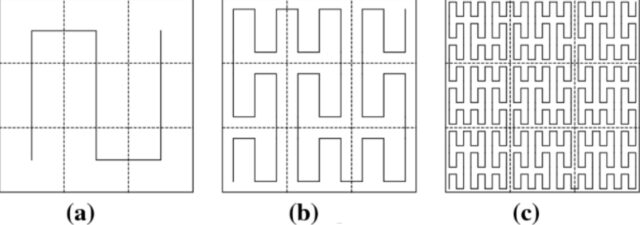
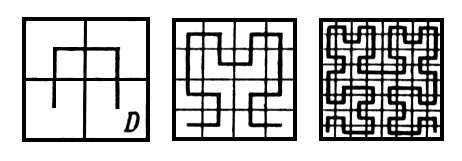
В 1890 году итальянский математик Джузеппе Пеано построил непрерывную кривую, которая проходит через любую точку квадрата (в оригинале использовался единичный, но построение легко повторить для квадрата любых размеров). Пеано задавался вопросом: может ли кривая заполнить всю плоскость или пространство? Результат Пеано воспринимался контринтуитивно. Годом позже кривую с тем же свойством построил уже графически Давид Гильберт.
В дальнейшем все кривые со свойством «заполнения» квадрата стали называть кривыми Пеано, а в более узком смысле это название закрепилось за конкретной кривой из его статьи 1890 года. Поскольку кривая заполняет любой наперед заданный квадрат, мы можем использовать ее и для заполнения плоскости, а в более общем случае — пространства или пустоты внутри нас.
Здесь нужно сделать важное уточнение — отображение с отрезка на квадрат, построенное Пеано, не взаимно-однозначно: не существует кривых Пеано, в которых каждая точка квадрата проходится только единожды — везде при этом построении возникают кратные точки.
Однако существуют кривые Пеано, у которых каждая точка проходится не более трех раз (и множество таких точек счетно).
Интересный факт следует из наших построений. Можно задать параметрически пространственную дугу, которая при проецировании на горизонтальную плоскость будет давать сплошное пятно; при этом такая «крыша» будет давать тень от вертикальных лучей света, но не спасет от дождя, поскольку ее поверхность получается не сплошной.
Ни одна кривая Пеано не гладкая. На интуитивном уровне можно объяснить это необходимостью очень быстро разворачивать направление нашей кривой, что невозможно сделать гладко. Сам Пеано в первой работе на эту тему сознательно не приводил построение кривой, чтобы не опираться на рисунок, однако мы всё же приведем это построение:
Обратите внимание на клетки, они позволяют понять, что происходит на каждом участке. То, что получится в результате бесконечного процесса этого рода, и называется кривой Пеано.
Обладающую тем же свойством кривую построил и современник Пеано Гильберт. Его кривая строится следующим образом:
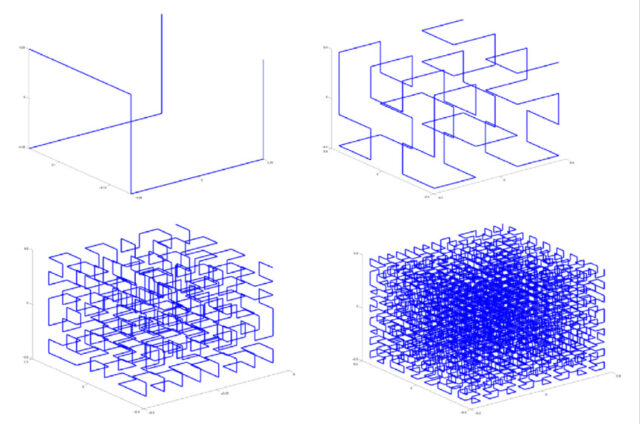
Существуют и объемные, и многомерные аналоги кривой Пеано, заполняющие куб (многомерный куб, соответственно).
Приведем несколько примеров других кривых, обладающих этим свойством.


Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Фракталы
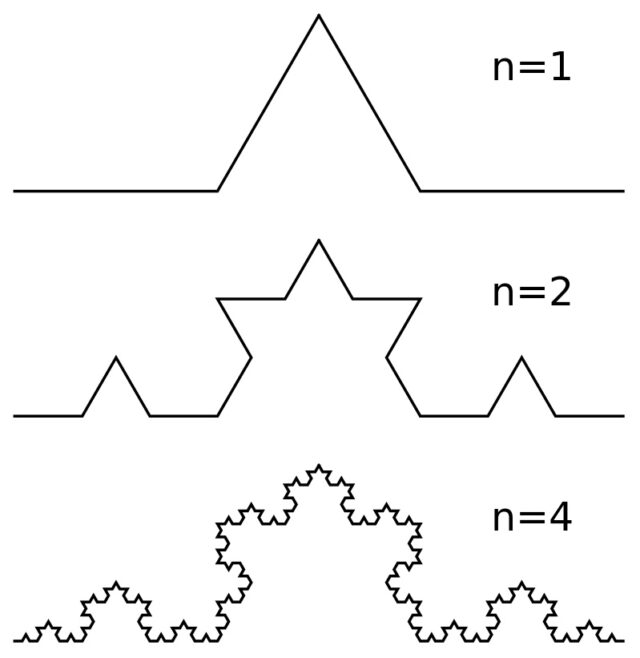
Подробнее об этом виде кривых мы писали тут. Однако в рамках разговора об эволюции представлений о кривых не упомянуть их невозможно. Классическим примером фрактала (фигуры со свойством самоподобия) является кривая Коха.
Свойство самоподобия означает, что фигура полностью или приближенно совпадает по форме с частью самой себя. В качестве примера можно провести кривую Коха:
В качестве нулевого «поколения» берем просто отрезок. На первом шаге его среднюю треть превращаем в правильный треугольник без основания, как бы выгибаем его. У нас получится четыре соединенных в кривую линию отрезка. На следующем шаге повторяем эту операцию с каждым из четырех отрезков. И так далее до бесконечности.
Читайте также
Наш подход с прямыми отрезками терпит здесь фиаско — вместо приближения к какой-то конечной длине сумма длин отрезков неограниченно растет.
Конечно, кривые, обладающие этим свойством, не исчерпываются самоподобными фигурами. Достаточно найти трещину на стене не самой простой формы: самоподобия в ней мы, как правило, не наблюдаем, и в то же время от одной ее «ветки» отходят новые, иной формы, и т. д.
Интересно, что тотально (то есть на любой порции) неспрямляемая кривая очень плохо помещается в ту же концепцию кривой как траектории движения. Точка, движущаяся по такой траектории, очевидно движется не по законам классической механики.
Во-первых, если бы точка двигалась с конечной скоростью по такой кривой, то она бы не двигалась вовсе: сколь угодно малая дуга здесь имеет бесконечную дугу. Но более того — такая кривая нигде не имеет и касательной, а значит, и направление скорости не задано!
В этом кратком обзоре мы лишь немного коснулись трансформации интуитивного представления о кривой в анализе — оставив за скобками развитие этого понятия в алгебре или современной геометрии, равно как и все вопросы, связанные с исследованием строения кривых.
Если эти — опущенные здесь — вопросы заинтересовали вас, то рекомендуем обратиться, например, к популярной брошюре В. И. Арнольда «Вещественная алгебраическая геометрия», а также к брошюре В. В. Острика и М. А. Цфасмана «Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые».
🔥 Видео
1 2 1 деление окружностиСкачать

Что такое радиан?Скачать

Как считали число пи? [Veritasium]Скачать
![Как считали число пи? [Veritasium]](https://i.ytimg.com/vi/A3PL61fHzjs/0.jpg)
Физика - движение по окружностиСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

8 класс, 32 урок, Касательная к окружностиСкачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Что такое число Пи? Кто его изобрел и почему оно так важноСкачать