Что такое величина треугольника

Метки

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Натуральная величина треугольника с описанием.

Натуральная величина треугольника определяется 2 методами:

1. замена плоскостей проекции;
2. плоскопараллельное перемещение.

Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».

Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.

Алгоритм определения натуральной величины плоскости:

Замена плоскостей проекции

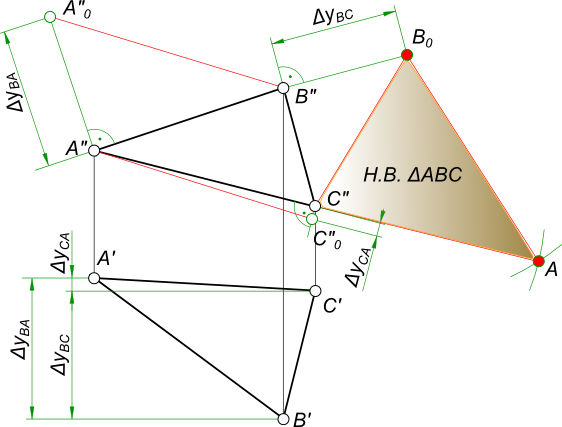
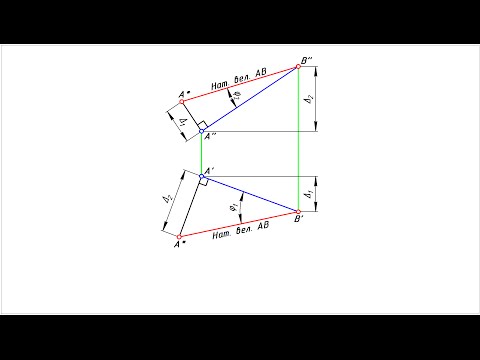
1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.

2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.

3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:

• от С2 до оси Х;
• от В2 до оси Х;
• от А0 до оси Х.

Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.

4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.

5.) Отмеряются расстояния:

• от В1 до Х1;
• от С1 до Х1;
• от А1 до Х1.

Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

6.) Соединяются точки и подписывают полученную плоскость заглавными «Н.В.»

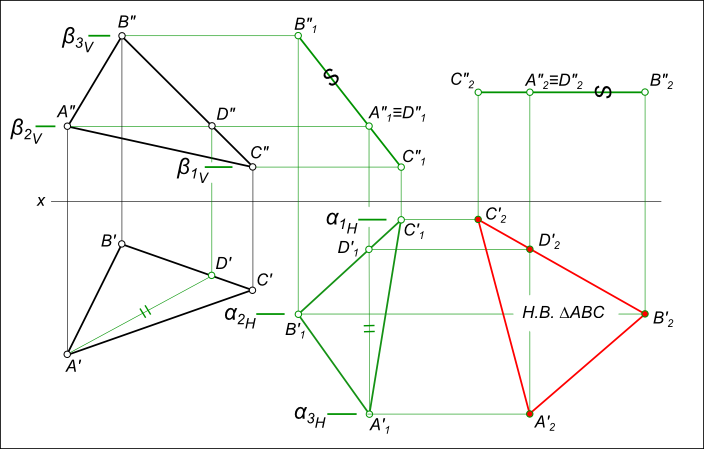
Плоскопараллельное перемещение

7.) Откладывается отрезок на оси Х (обозначен синим цветом).

8.) Переносятся точки на текущее построение.

9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости. 12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:

Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).

13.) Соединяются и подписываются точки (А1′, В1′ и С1′). Опускают прямые от С2″ и А2″14.) От точек С1 и А1 отводят прямые до пересечения с прямыми опущенными от точек С2″ и А2″. В месте пересечения ставится точка.15.) Завершающим шагом является соединение точек и обводка линиями всего чертежа.Пример чертежа на тему «Натуральная величина треугольника» смотрите здесь.

Видео:Натуральная величина треугольника (метод вращения)Скачать

Построить натуральную величину треугольника авс

Натуральная величина треугольника на эпюре Монжа может быть определена: – способом прямоугольного треугольника;

Здесь поочередно применяется способ прямоугольного треугольника для определения действительных величин отрезков, составляющих треугольник, а затем, к одному из них методом засечек строятся два других.

Используем Метод преобразования проекций для определения истиной величины треугольника на эпюре Монжа:

– Способ вращения вокруг осей перпендикулярных плоскостям проекций;

– Вращение вокруг горизонтали представляющих собой линии уровня;

представляющих собой линии уровня;

– Вращение вокруг следа или способ совмещения с плоскостью проекций;

Задача на определение натуральной величины плоской фигуры относится к разделу метрические задачи.

Ниже приведены решения одной и той же задачи вышеописанными методами.

9.6.1. Задание:определить натуральную величину треугольника ABC(рис. 9.8), а также угол наклона плоскости треугольника к плоскости П_1.

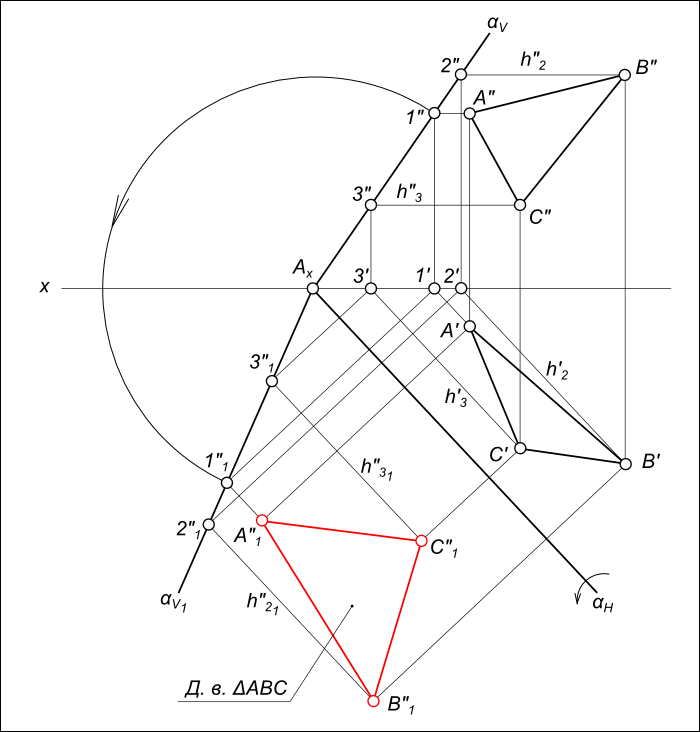
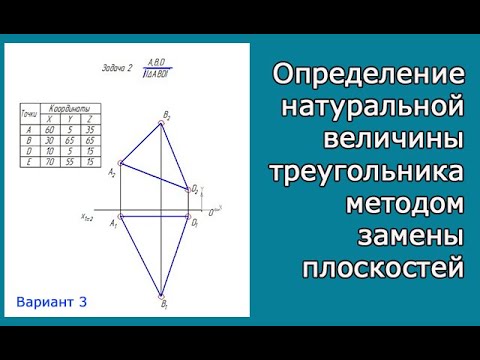
1) Решение методом замены плоскостей проекций (рис. 9.9).

Плоскость треугольника спроецируется в натуральную величину в том случае, если она будет параллельна одной из плоскостей проекций. Одним преобразованием задачу решить невозможно. Она решается в два этапа: при первой замене плоскостей проекций получают плоскость треугольника ABC,перпендикулярную к новой плоскости проекций, при второй замене – получают плоскость треугольника, параллельную новой плоскости проекций.

Первый этап. Одним из условий перпендикулярности двух плоскостей является наличие прямой, принадлежащей одной из плоскостей, перпендикулярной к другой плоскости. Используя этот признак, проводят через точку А в плоскости треугольника горизонталь (h). Затем на произвольном расстоянии от горизонтальной проекции треугольника A₁B₁C₁ проводят ось x_1,4новой системы плоскостей проекций П₁/П₄перпендикулярно к горизонтальной проекции горизонтали h₁.В новой системе треугольник ABC стал перпендикулярен к новой плоскости проекций П₄.

На линиях проекционной связи в новой системе откладывают координатыzточек А, В, С с фронтальной проекции исходной системы плоскостей П₁/П₂.

При соединении новых проекций А₄,B₄, С₄получают прямую линию, в которую спроецировался треугольник ABC. На этом этапе определяется угол наклона плоскости треугольника к горизонтальной плоскости проекции П₁ – угол α. На чертеже это угол между осью x_1,4и проекцией С₄А₄В₄.

Второй этап. Выбираем новую плоскость проекции П₅,параллельную плоскости треугольника, т.е. новую ось x_4,5проводят параллельно С₄А₄В₄на произвольном расстоянии. Получают новую систе­му П₄/П₅.Полученный треугольник А₅В₅С₅и есть искомая натуральная величина треугольника ABC.

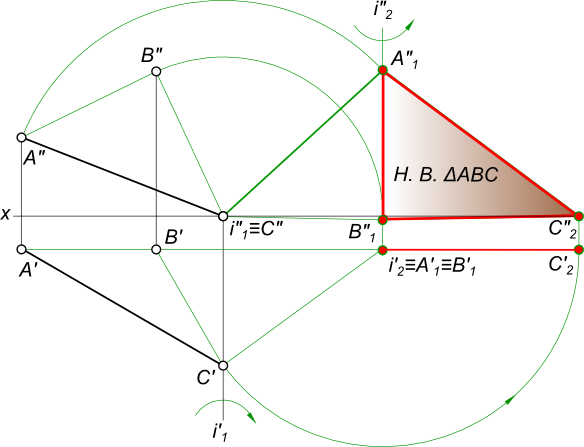
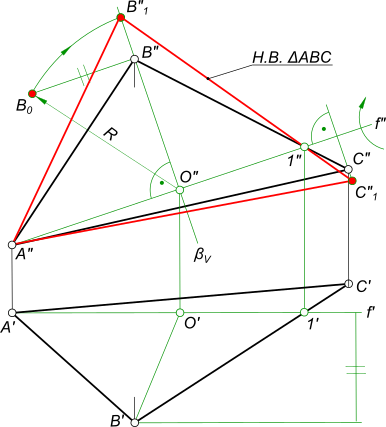
2) Решение методом вращения вокруг проецирующей оси(рис. 9.10).

Задача решается в два этапа. На первом этапе выполняют вращение так, чтобы плоскость треугольника ABCпреобразовалась в проецирующую плоскость, т.е. стала перпендикулярна к одной из плоскостей проекций. Для этого проводят горизонталь h (h₁,h₂) через точку А. (построение начинают с фронтальной проекции h₂,она проходит через проекцию точки A₂и проекцию точки 1₂ при этомh₂ параллельна оси х).Далее находят горизонтальную проекцию h₁ горизонтали h (через проекции A₁ и 1₁). Через точку А проводят ось i – ось вращения треугольника так, чтобы она была перпендикулярна к П₁. На фронтальной проекции через вершины А₂ и В₂ проводят следы горизонтальных плоскостей уровня Δ и Σв которых при вращении будут перемещаться точки АиВ. Вершина С принадле­жит плоскости П₁поэтому ее плоскостью вращения будет плоскость проекций П₁.На горизонтальной проекции, взяв за центр вращения проекцию i₁ поворачивают горизонталь А так, чтобы на плоскость П₂ она спроецировалась в точку. На чертеже это выразится 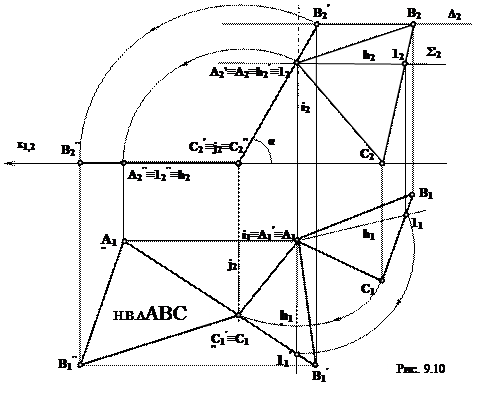тем, что h’₁ займет новое положение – перпендикулярно к оси х.

При этом на фронтальной проекции А₂ остается неизменной, находясь на следе плоскости Σ₂ и ее обозначим a₂‘.

На гори­зонтальной проекции поворачиваем оставшиеся вершины В и С во­круг оси i так, чтобы . На фронтальной проекции вершина В перемещается по следу плоскости ₂, а вершина С – по оси х. Соединив новые положения проекций всех вершин треугольника ABC, получают проекцию А’₂В’₂С’₂,сливающуюся в линию. Плоскость треугольника ABC заняла проецирующее положение. На данном этапе, при необходимости, находят угол наклона плоскости треугольника ABC к П₁ – угол α .

На втором этапе проводят ось jчерез вершинуС так, чтобы ось была фронтально проецирующая. При этом С’₂ ≡ j’₂, а горизонтальная проекция j’₁ пройдет через проекцию С’₁. Вокруг оси поворачивают треугольник так, чтобы он стал параллелен горизонтальной плоскости проекций. В данной задаче вращают точки А’₂ и В’₁, вокруг j₂ до совмещения с осью х,при этом проекции B’₁ и A’₁ будут перемещаться параллельно оси хи займут новое положение В»₁, и А»₁ вершина С оста­нется на месте. Соединив точки между собой, получают новое положение плоскости (оно соответствует натуральной величине треугольника ABC).

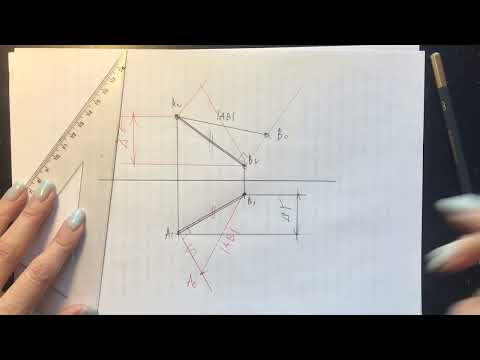
3) Решение методом плоскопараллельного перемещения (рис. 9.11).

Задача решается в два этапа. На первом этапе преобразуют чертеж так, чтобы плоскость треугольника ABC стала перпендику­лярна к одной из плоскостей проекций. Для этого проводят в плоскости треугольника горизонталь h (фронтальная проекция А₂1₂║х,). Каждую вершину треугольника заключают в свою плоскость уровня, параллельную плоскости П₁. В рассматриваемом примере вершина С принадлежит плоскости проек­ций П₁, А принадлежит плоскости Σ, В — плоскости Δ.

Плоскость треугольника перемещается в пространстве до тех пор, пока горизонталь h₁ треугольника не станет перпендикулярна к фронтальной плоскости проекций П₂.

Для этого на свободном поле чертежа вычерчивают горизонтальную проекцию треугольника A₁ ′ B₁ ′ C₁ ′ с условием, чтобы А₁1₁П₂, а значит А₁ ′ 1₁ ′ х. При этом вершины треугольника, перемещаясь каждая в своей плоскости, займут новое положение – (фронтальная проекция А₂В₂С₂ заменится А’₂В’₂С’₂).Соединив эти точки, получают новое положение треугольника ABC, спроецированного в линию, т.е. перпендикулярного к плоскости П₂.

На втором этапе, чтобы получить натуральную величину треугольника ABC, его плоскость поворачивают до тех пор, пока она не будет параллельна одной из плоскостей проекций. В рассматриваемом решении фронтальную проекцию треугольника А₂‘В₂‘С₂‘располагают на произвольном расстоянии от оси хпараллельно плоскости П₁. При этом вершины А, Ви С треугольника заключают в горизонтально проецирующие плоскости θ, Т, Р. По следам этих плоскостей будут перемещаться горизонтальные проекции вершин А₁‘В₁‘С₁‘. От нового положения фронтальной проекции А₂«В₂«С₂« проводят линии проекционной связи до пресечения с соответствующими следами плоскостей, в которых они перемещаются (θ₁,T₁,P₁), и получая проекции точек А₁» В₁» C₁«. Соединив эти проекции, получают тре­угольник ABC в натуральную величину.

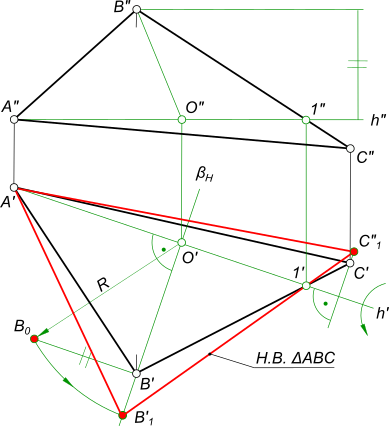
4) Решение методом вращения вокруг линии уровня(рис.9.12)

Для решения задачи этим способом необходимо повернуть плоскость треугольника вокруг линии уровня, в данном случае вокруг горизонтали, до положения, параллельного горизонтальной плоскости проекции. Через точку А в плоскости треугольника ABC проводят горизонталь h, фронтальная проекция которой будет параллельна оси х. Отмечают точку 1₂ и находят ее горизонтальную проекцию 1₁. Прямая A₁1₁ является горизонтальной проекцией h₁горизонтали h. Вокруг горизонтали будут вращаться точки В и С. Определяют натуральную величину радиуса вращения точки С .

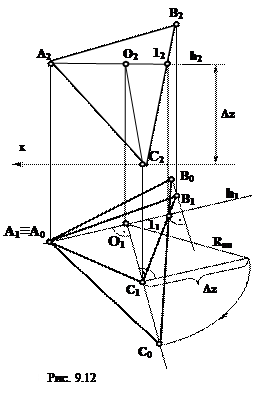
Для определения натуральной величины радиуса вращения используют любой метод (в данном случае способ прямоугольного треугольника) строят прямоугольный треугольник, в котором O₁C₁ – один из катетов. Вто­рой катет – разность координат Δzотрезка О₂С₂, взятого с фронталь­ной проекции. В построенном треугольнике гипотенуза O₁C – нату­ральная величина радиуса вращения.

На продолжении перпендикуляра O₁C₁ откладывают |R_Bp.| и полу­чают новое положение вершины С после вращения — С . Проекция вер­шины В получается пересечением луча C 1₁ и перпендикуляра к горизонтальной проекции h₁ проведенного через проекцию точки В₁.

Треугольник A B C есть искомая натуральная величина тре­угольника ABC.

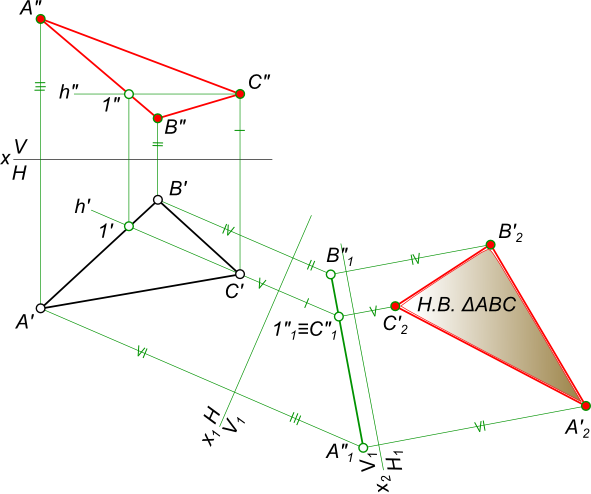
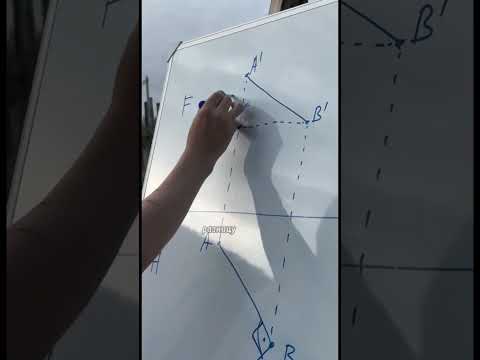
5) Решение методом совмещения(рис. 9.13).

Для решения задачи методом совмещения необходимо построить следы плоскости Σ, которой принадлежит треугольник ABC. Для этого проводят в плоскости треугольника ABC фронталь f и находят горизонтальный след этой фронтали – N₁. По условию задачи вершина С треугольника принадлежит горизонтальной плоскости проек­ций П₁. Тогда горизонтальный след Σ₁ плоскости Σпроводят через проекции N₁ и C₁. Соединив эти две точки и продлив отрезок до пересечения с осью х, находят точку схода следов Σ_х. Учитывая, что все фронтали плоскости параллельны ее фронтальному следу, фронтальный след Σ₂ плоскости Σпроводят через точку Σ_хпараллельно проекции фронтали f₂.

Для нахождения натуральной величины треугольника ABCнеобходимо построить совмещенное положение плоскости Σ с горизонтальной плоскостью проекций П₁. Для этого через вершину Апроводят горизонталь h₁. На фронтальном следе Σ₂ фиксируют точку 2₂. Ее горизонтальная проекция – точка 2₁. Точка 2 вращается в плоскости, перпендикулярной к горизонтальному следу плоскости Σ. Поэтому, чтобы построить точку 2 в совмещенном положении 2 , проводят из 2₁перпендикуляр к горизонтальному следу Σ, а из центра Σ_х дугу окружности радиусом Σ_х2₂ до пересечения с направлением перпендикуляра. Соединив Σ_х с 2 , получают совмещенное положение фронтального следа Σ – Далее через точку 2 проводят горизонталь h всовмещенном положении. На этой горизонтали находят точку А , проведя перпендикуляр из точки A₁ к горизонтальному следу Σ₁.

По такой же схеме строят совмещенное положение точки В . Совмещенное положение точки С совпадает с ее горизонтальной проекцией С₁ т.е. С₁≡С . Соединив построенные точки, получают треугольник А В С – это и есть натуральная величина треугольника ABC.

Не нашли то, что искали? Воспользуйтесь поиском:

Метки

Видео:Построение натуральной величины треугольника методом вращенияСкачать

Натуральная величина треугольника с описанием.

Натуральная величина треугольника определяется 2 методами:

1. замена плоскостей проекции;
2. плоскопараллельное перемещение.

Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».

Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.

Алгоритм определения натуральной величины плоскости:

Замена плоскостей проекции

1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.

2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.

3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:

• от С2 до оси Х;
• от В2 до оси Х;
• от А0 до оси Х.

Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.

4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.

5.) Отмеряются расстояния:

• от В1 до Х1;
• от С1 до Х1;
• от А1 до Х1.

Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

6.) Соединяются точки и подписывают полученную плоскость заглавными «Н.В.»

Плоскопараллельное перемещение

7.) Откладывается отрезок на оси Х (обозначен синим цветом).

8.) Переносятся точки на текущее построение.

9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости. 12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:

Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).

13.) Соединяются и подписываются точки (А1′, В1′ и С1′). Опускают прямые от С2″ и А2″14.) От точек С1 и А1 отводят прямые до пересечения с прямыми опущенными от точек С2″ и А2″. В месте пересечения ставится точка.15.) Завершающим шагом является соединение точек и обводка линиями всего чертежа.Пример чертежа на тему «Натуральная величина треугольника» смотрите здесь.

Видео:Натуральная величина отрезкаСкачать

Треугольник. Формулы и свойства треугольников.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Типы треугольников

По величине углов

По числу равных сторон

Видео:Определение длины отрезкаСкачать

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Видео:Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Видео:Нахождение натуральной величины отрезка методом прямоугольного треугольникаСкачать

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Видео:Нахождение натуральной величины треугольника. Метод замены плоскостей проекцийСкачать

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Видео:Найти натуральную величину отрезка с помощью прямоугольного треугольника. #отрезка #геометрияСкачать

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Видео:Начертательная геометрия. Определение натуральной величины треугольникаСкачать

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Видео:Определение натуральной величины треугольника АВD методом замены плоскостей проекции.Скачать

Связь между вписанной и описанной окружностями треугольника

Видео:Начерталка - Определение натуральной величины треугольника АВССкачать

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Видео:Определение натуральной величины треугольника способом плоскопараллельного перемещения #решениезадачСкачать

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Видео:Построение натуральной величины треугольника АВС методом триангуляцииСкачать

Формулы площади треугольника

Формула Герона

Видео:Метод вращения вокруг горизонтали. Натуральная величина треугольникаСкачать

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Видео:[Начертательная геометрия для "чайников" 1 курс] Натуральная величина треугольникаСкачать

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

🔥 Видео

Определение натуральной величины треугольника методом замены плоскостей #начертательнаягеометрияСкачать

Задача №1 Определение натуральной величины отрезка прямой (АВ) методом прямоугольного треугольникаСкачать

Определение натуральной величины треугольника АВС методом совмещенияСкачать