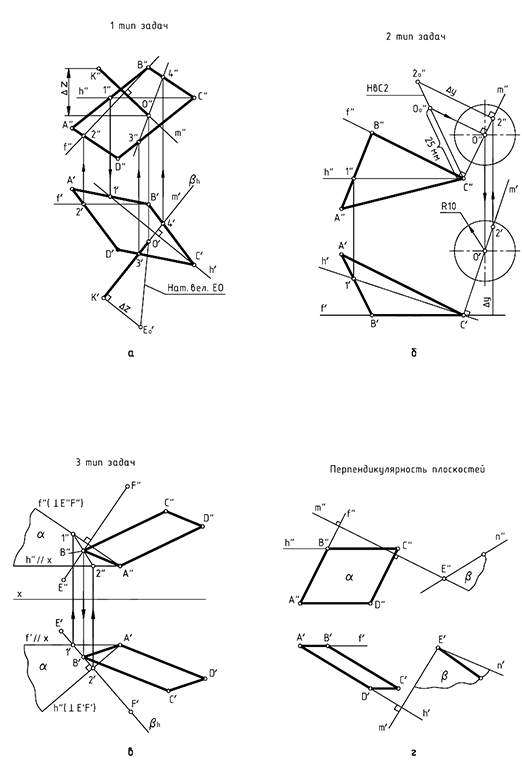
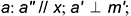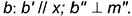Контрольные задания по теме: Рабочая тетрадь задача 44, задача 45
Построение взаимно перпендикулярных прямых и плоскостей является важной графической операцией при решении метрических задач.
Построение перпендикуляра к прямой или плоскости основывается на свойстве прямого угла, которое формулируется следующим образом: если одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то угол проецируется в натуральную величину на эту плоскость.
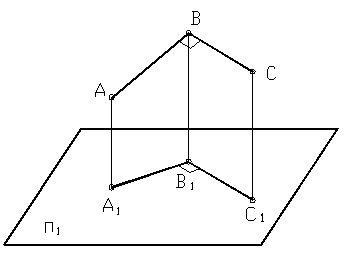
Рисунок 28
Сторона ВС прямого угла АВС, изображенного на рисунке 28, параллельна плоскости П 1 . Следовательно, проекция угла АВС на эту плоскость будет представлять прямой угол А 1 В 1 С 1 =90.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. При построении перпендикуляра из множества прямых принадлежащих плоскости, выбирают прямые уровня — горизонталь и фронталь. В этом случае горизонтальную проекцию перпендикуляра проводят перпендикулярно горизонтали, а фронтальную -перпендикулярно фронтали. На примере, изображенном на рисунке 29, показано построение перпендикуляра к плоскости, заданной треугольником АВС, из точки К. Для этого сначала проводим горизонталь и фронталь в плоскости. Затем из фронтальной проекции точки К проводим перпендикуляр к фронтальной проекции фронтали, а из горизонтальной проекции точки – перпендикуляр к горизонтальной проекции горизонтали. Затем строим точку пересечения данного перпендикуляра с плоскостью при помощи вспомогательной секущей плоскости Σ. Искомая точка – F. Таким образом, полученный отрезок КF является перпендикуляром к плоскости АВС.
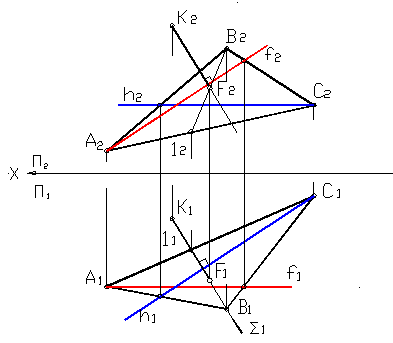
Рисунок 29
На рисунке 29 изображено построение перпендикуляра КF к плоскости АВС.
Две плоскости перпендикулярны, если прямая, лежащая в одной плоскости, перпендикулярна двум пересекающимся прямым другой плоскости. Построение плоскости перпендикулярной данной плоскости АВС показано на рисунке 30. Через точку М проводится прямая МN, перпендикулярная плоскости АВС. Горизонтальная проекция этой прямой перпендикулярна АС, так как АС является горизонталью, а фронтальная проекция перпендикулярна АВ, так как АВ – фронталь. Затем через точку М проводится произвольная прямая EF. Таким образом, плоскость перпендикулярна АВС и задана двумя пересекающимися прямыми EF и MN.
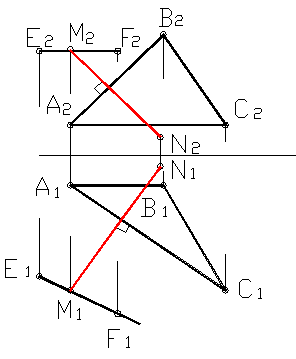
Рисунок 30
Этот способ применяется для определения натуральных величин отрезков общего положения, а также углов наклона их к плоскостям проекций. Для того, чтобы определить натуральную величину отрезка этим способом, необходимо достроить прямоугольный треугольник к одной из проекций отрезка. Другим катетом будет являться разность высот или глубин конечных точек отрезка, а гипотенуза – натуральной величиной.
Рассмотрим пример: на рисунке 31 дан отрезок АВ общего положения. Требуется определить его натуральную величину и углы его наклона к фронтальной и горизонтальной плоскостям проекций.
Проводим перпендикуляр к одному из концов отрезка на горизонтальной плоскости. Откладываем на нем разность высот (ZA-ZB) концов отрезка и достраиваем прямоугольный треугольник. Гипотенуза его является натуральной величиной отрезка, а угол между натуральной величиной и проекцией отрезка – натуральной величиной угла наклона отрезка к плоскости П 1 . Порядок построений на фронтальной плоскости тот же самый. По перпендикуляру откладываем разность глубин концов отрезка (YA-YB). Полученный угол между натуральной величиной отрезка и его фронтальной проекцией – это угол наклона отрезка к плоскости П 2 .
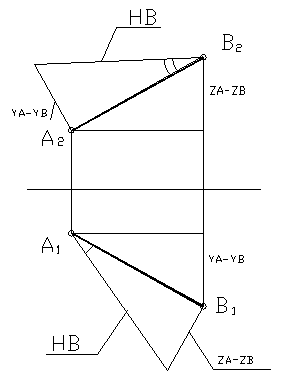
Рисунок 31
1. Сформулируйте теорему о свойстве прямого угла.
2. В каком случае прямая перпендикулярна плоскости?
3. Сколько прямых и сколько плоскостей, перпендикулярных данной плоскости, можно провести через точку пространства?
4. Для чего применяется способ прямоугольного треугольника?
5. Как при помощи этого способа определить угол наклона отрезка общего положения к горизонтальной плоскости проекций?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Видео:Параллельность прямой к плоскостиСкачать

Перпендикулярность геометрических объектов в начертательной геометрии с примерами
Содержание:
Проецирование прямого угла:
В общем случае плоский угол проецируется на плоскость проекций с искажением.
Теорема о проецировании прямого угла:
Прямой угол на плоскость проекций проецируется без искажения, если, по крайней мере, один из его лучей параллелен этой плоскости проекций.
Пусть прямые
1)
2)
3)
Все прямые, лежащие в плоскости 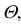
Видео:Перпендикуляр к плоскостиСкачать

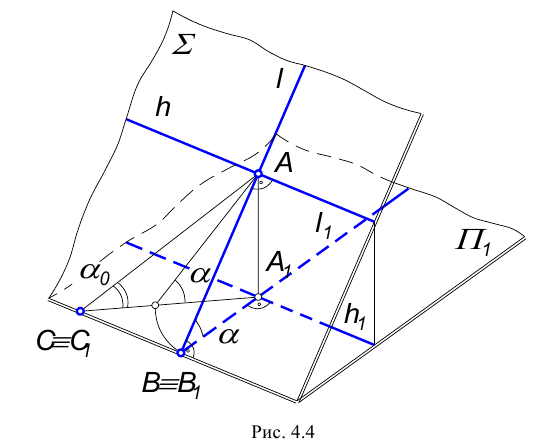
Линия наибольшего наклона плоскости
Прямая, лежащая в плоскости и образующая с плоскостью проекций наибольший угол, называется линией наибольшего наклона плоскости.
Линии наибольшего наклона перпендикулярны к соответствующим линиям уровня.
Угол между линией наибольшего наклона и плоскостью проекций равен углу наклона самой плоскости к этой плоскости проекций. Поэтому с помощью этой линии определяют двухгранные углы между заданной плоскостью и соответствующими плоскостями проекций.
Прямые, лежащие в плоскости и перпендикулярные соответствующим линиям уровня плоскости, являются линиями наибольшего наклона..
Возьмем плоскость общего положения 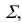
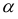
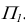
В результате построений угол 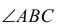
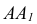
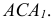
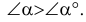
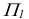
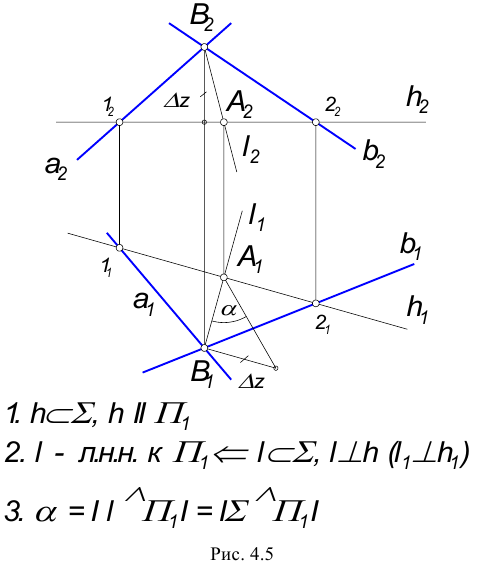
Пример: Определить действительную величину угла наклона плоскости 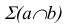
Аналогично находятся углы наклона плоскости к фронтальной и профильной плоскостям проекций: л.н.н. к фронтальной плоскости проекций перпендикулярна фронтали плоскости, а л.н.н. к профильной плоскости проекций – профильной прямой плоскости.
Видео:ПЕРПЕНДИКУЛЯР К ПЛОСКОСТИ ЗАДАННОЙ ПАРАЛЛЕЛЬНЫМИ ЛИНИЯМИ. Начертательная геометрияСкачать

Перпендикулярность прямой и плоскости
Из курса элементарной геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Но, исходя из теоремы о проецировании прямого угла, перпендикуляр, проведенный к прямым общего положения, на КЧ проецируется с искажением. Поэтому применительно к начертательной геометрии признак перпендикулярности прямой и плоскости формулируется следующим образом:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся линиям уровня этой плоскости.
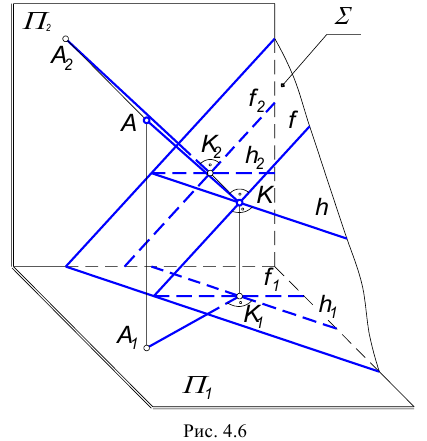
Это связано с тем, что только к линиям уровня на плоскостях проекций можно построить прямой угол без искажения (см. § 4.1). В качестве линий уровня плоскости, при решении задач на перпендикулярность геометрических объектов, обычно выбирают горизонталь и фронталь. Возьмем плоскость общего положения 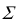
На основании теоремы о проецировании прямого угла горизонтальная проекция перпендикуляра к плоскости общего положения на КЧ располагается перпендикулярно горизонтальной проекции горизонтали плоскости, а, следовательно, и к ее горизонтальному следу, а фронтальная проекция перпендикуляра – фронтальной проекции фронтали и фронтальному следу.
Пример: Из точки А провести перпендикуляр к плоскости 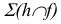
Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Перпендикулярность плоскостей
Признак перпендикулярности плоскостей:
Плоскость перпендикулярна другой, если она проходит через перпендикуляр к этой плоскости.
Плоскость перпендикулярна другой плоскости, если она перпендикулярна прямой, лежащей в этой плоскости.
Итак, зная, как располагаются проекции прямой, перпендикулярной плоскости, легко строить взаимно-перпендикулярные плоскости. Исходя их признака перпендикулярности плоскостей можно:
- построить перпендикуляр к заданной плоскости и через него провести искомую плоскости или
- в заданной плоскости взять прямую и перпендикулярно ей провести искомую плоскость.
В любом из этих случаев задача будет иметь бесчисленное множество решений, если на искомую плоскость не наложены дополнительные условия. Рассмотрим два примера построения перпендикулярных плоскостей.
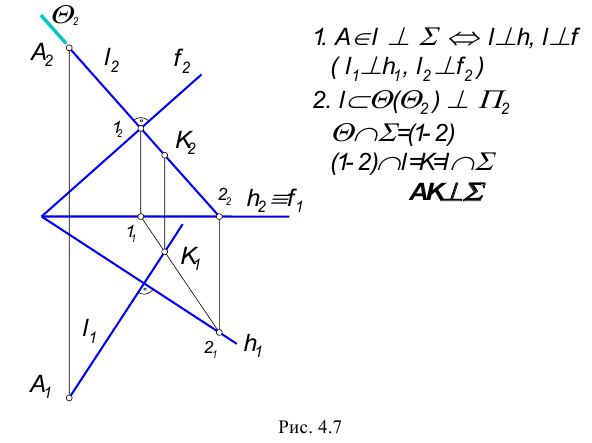
Пример: Через точку А провести плоскость, перпендикулярную плоскости
Новая плоскость задана двумя пересекающимися прямыми, одна из которых отвечает условию перпендикулярности плоскостей (прямая 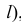
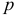
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод замены плоскостей проекций
- Проецирование прямой линии
- Проецирование плоскости
- Плоскость на эпюре Монжа
- Построение линии пересечения поверхностей
- Проецирование прямой
- Взаимное положение плоскостей, прямой линии и плоскости
- Взаимное расположение точки, прямых и плоскостей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Перпендикуляр к плоскостиСкачать
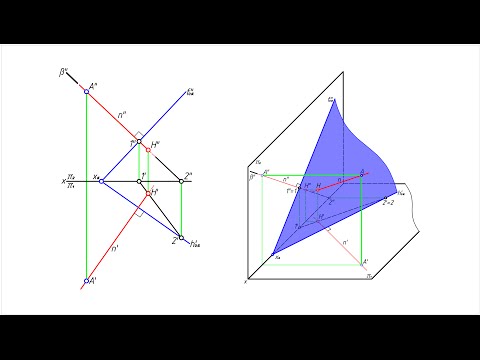
Перпендикулярность
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Перпендикулярность
Решение задач на тему перпендикулярности прямой и плоскости основано на двух теоремах геометрии:
- 1-я теорема: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
- 2-я теорема: о проекции прямого угла (изложена выше — см. рис. 2.14, 2.15 и 2.16) — если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то на эту плоскость проекций угол проецируется прямым.
Из этих двух теорем следует, что на чертеже проекции перпендикуляра к плоскости можно провести только к проекциям фронтали и горизонтали, то есть к двум пересекающимся прямым уровня, которые можно провести в плоскости.
- фронтальная проекция
прямой, перпендикулярной прямой к плоскости, перпендикулярна к фронтальной проекции
фронтали этой плоскости
;
- горизонтальная проекция
прямой, перпендикулярной прямой к плоскости, перпендикулярна к горизонтальной проекции
горизонтали этой плоскости
.
Задачи на тему перпендикулярности прямой и плоскости можно разделить на три группы:
1-я группа. Провести от точки, лежащей в плоскости, перпендикуляр в пространство.
2-я группа. Провести из точки, не лежащей в плоскости, перпендикуляр к этой плоскости.
3-я группа. Построить плоскость, перпендикулярную к прямой общего положения (построить геометрическое место точек — ГМТ).
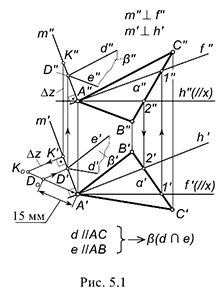
Первая группа задач требует по условию проведения перпендикуляра от плоскости (восставить перпендикуляр) в пространство (см. рис. 5.1).
В этой группе задач требуется, как правило, построить на проведенном перпендикуляре проекции отрезка заданной величины. Графические действия по построению проекций отрезка заданной величины на проекциях прямой общего положения изложены ранее (см. рис. 2.9).
На рисунке 5.1 показано решение примерной задачи первой группы: построить плоскость 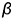
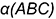
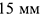
Эта задача относится к первой группе, поскольку для построения параллельной плоскости 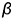
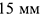
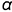
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Провести в заданной плоскости общего положения 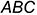
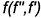
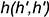
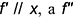
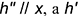
2-е действие. Провести от точки плоскости, например, от вершины 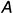
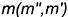
- фронтальную проекцию
перпендикулярно
;
- горизонтальную проекцию
перпендикулярно
.
3-е действие. На проекциях перпендикуляра 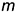
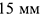
- Ограничить построенную прямую
произвольным отрезком
.
- Построить натуральную величину этого отрезка (см. рис. 5.1) способом прямоугольного треугольника — это гипотенуза
.
- На построенной гипотенузе отложить заданную величину
и построить проекции отрезка
заданной величины (см. построения), то есть проекции точки
, находящейся на расстоянии
от плоскости
.
4-е действие. Построить плоскость 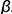
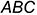
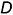
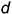
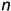
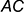

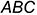
то есть
Вторая группа задач требует по условию проведения перпендикуляра из точки в пространстве к плоскости (опустить перпендикуляр). В этой группе задач, как правило, требуется построить точку пересечения построенного перпендикуляра с заданной плоскостью.
Построение точки пересечения прямой общего положения с плоскостью общего положения было рассмотрено выше (см. рис. 4.6).
На рис. 5.2 показано решение примерной задачи второй группы: определить расстояние от точки 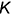
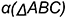
Эта задача относится ко второй группе, так как расстояние от точки 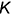
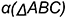
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Провести в плоскости фронталь 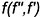
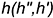
2-е действие. Провести через заданную точку 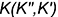
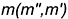
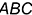
перпендикулярно
;
перпендикулярно
.
3-е действие. Построить точку пересечения 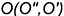
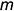
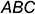
- Заключить прямую
во вспомогательную горизонтально-проецирующую плоскость
- Построить вспомогательную линию пересечения 3-4 заданной плоскости
со вспомогательной плоскостью
:
— определяется на следе
;
— строится по принадлежности точек 3 и 4 сторонам
и
треугольника
;
- Определить проекции искомой точки пересечения
на пересечении проекций построенной вспомогательной линии пересечения 3-4 с проекциями перпендикуляра
.
4-е действие. Построить натуральную величину отрезка 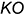
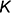
Третья группа задач требует по условию построения некоторой вспомогательной плоскости (геометрического места точек), перпендикулярной к прямой общего положения. Эту перпендикулярную плоскость можно задать двумя пересекающимися прямыми, каждая из которых должна быть перпендикулярна прямой общего положения (теорема о перпендикулярности прямой и плоскости, т. е. признак перпендикулярности прямой и плоскости). На чертеже плоскость, перпендикулярную к прямой общего положения, можно задать только проекциями пересекающихся прямых уровня — фронтальной (параллельной плоскости проекций 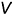
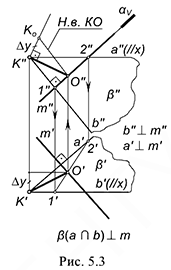
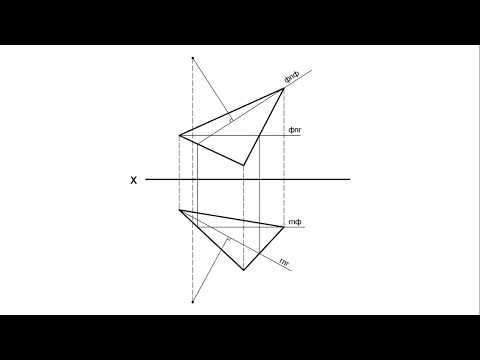
На рис. 5.3 показано решение примерной задачи третьей группы: определить расстояние от точки 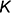
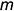
Эта задача относится к третьей группе, поскольку на чертеже провести перпендикуляр к прямой общего положения, по которому определяется расстояние от точки 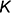
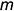
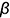
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Построить троим вспомогательную плоскость 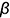
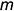
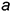
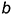
- горизонтальной прямой
- фронтальной прямой
2-е действие. Построить точку 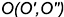
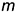

3-е действие. Соединить одноименные проекции точек 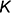

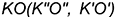
4-е действие. Построить натуральную величину построенного отрезка 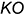
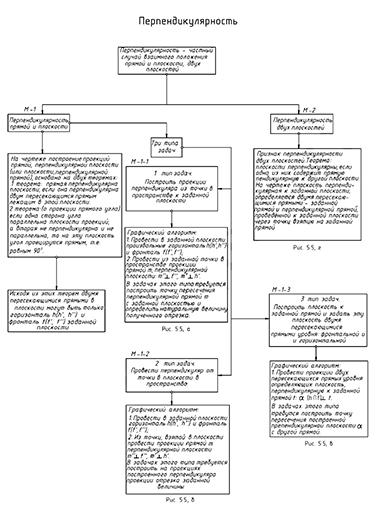
Структуризация материала пятой лекции в рассмотренном объеме схематически представлена на рис. 5.4 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 5.5).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎬 Видео
Параллельные прямые | Математика | TutorOnlineСкачать

Перпендикуляр от точки к плоскостиСкачать
45. Построение перпендикуляра к плоскости, заданной пересекающимися прямымиСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Построение следов плоскостиСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Перпендикулярные прямыеСкачать

Точка встречи прямой с плоскостьюСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

7 класс, 16 урок, Перпендикуляр к прямойСкачать

Перпендикуляр к прямой через заданную точку.Скачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

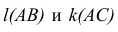
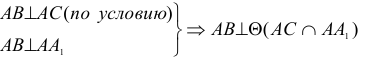
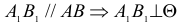
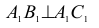
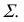
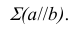
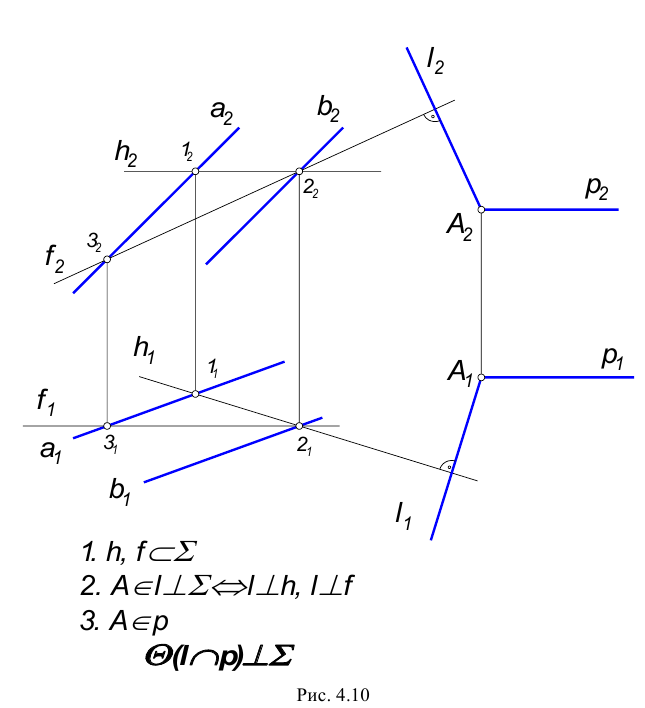

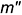 прямой, перпендикулярной прямой к плоскости, перпендикулярна к фронтальной проекции
прямой, перпендикулярной прямой к плоскости, перпендикулярна к фронтальной проекции 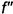 фронтали этой плоскости
фронтали этой плоскости 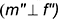 ;
;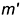 прямой, перпендикулярной прямой к плоскости, перпендикулярна к горизонтальной проекции
прямой, перпендикулярной прямой к плоскости, перпендикулярна к горизонтальной проекции 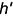 горизонтали этой плоскости
горизонтали этой плоскости 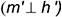 .
.
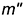 перпендикулярно
перпендикулярно 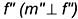 ;
;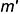 перпендикулярно
перпендикулярно 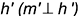 .
.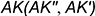 .
.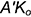 .
.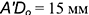 и построить проекции отрезка
и построить проекции отрезка 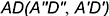 заданной величины (см. построения), то есть проекции точки
заданной величины (см. построения), то есть проекции точки 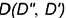 , находящейся на расстоянии
, находящейся на расстоянии 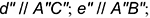
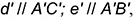 то есть
то есть 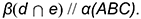
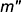 перпендикулярно
перпендикулярно 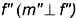 ;
;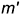 перпендикулярно
перпендикулярно 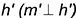 .
.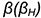
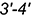 — определяется на следе
— определяется на следе 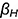 ;
;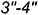 — строится по принадлежности точек 3 и 4 сторонам
— строится по принадлежности точек 3 и 4 сторонам 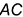 и
и 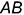 треугольника
треугольника