Как построить квадрат описанный вокруг окружности (7 видео)

РИСУНОК КВАДРАТА, ОПИСАННОГО ВОКРУГ ОКРУЖНОСТИ В ПЕРСПЕКТИВЕ

ЦЕЛЬ ЗАДАНИЯ. Научиться рисовать правильный квадрат в перспективе, описывая его вокруг окружности.

ПОСТАНОВКА ЗАДАНИЯ. Изобразите несколько горизонтальных и вертикальных окружностей в перспективе (эллипсов), опишите вокруг эллипсов квадраты в угловой и фронтальной перспективах.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Горизонтальная окружность. Нарисуйте окружность, лежащую на горизонтальной плоскости. Вы уже знаете, что на перспективном рисунке такая окружность изображается как эллипс, оси которого – горизонтальная и вертикальная прямые.

В угловой перспективе стороны горизонтального квадрата имеют две точки схода. Сначала задайте одно из направлений, соответствующее любым двум параллельным сторонам квадрата, а затем найдите второе, ему перпендикулярное. Для этого проведите прямую произвольного направления (среднюю линию квадрата) через центр окружности (рис. 2.18). Полученные на пересечении этой прямой с эллипсом точки 1 и 3 являются точками касания сторон квадрата к окружности. Проведите касательные через эти точки. Обратите внимание, что на рисунке полученные прямые (две стороны квадрата) сходятся в перспективе. Теперь проведите вторую среднюю линию квадрата, параллельную уже нарисованным сторонам (рис. 2.19). Она пройдет через центр окружности и даст нам на пересечении с эллипсом еще пару точек – 2 и 4. Эти точки также являются точками касания сторон квадрата к окружности. Проведите прямые, касательные к эллипсу в этих точках. Эти касательные параллельны прямой 7 – 3, т. е. уходят вместе с ней в одну точку схода на горизонте (рис. 2.20). Внимательно проверьте рисунок. В полученном квадрате прямые 1 – 3 и 2 – 4 параллельны соответствующим сторонам квадрата, а точки 1, 2, 3, 4 делят его стороны пополам. Проведите диагонали квадрата – они должны пересекаться в центре окружности.

Во фронтальной перспективе квадрат имеет две горизонтальные стороны и две стороны, сходящиеся в точке схода на линии горизонта. Построение такого квадрата ведется по той же схеме, что и построение квадрата в угловой перспективе. Средняя линия 1 – 3 совпадает с малой осью эллипса. Изобразите горизонтальные стороны квадрата как касательные к эллипсу в точках 1 и 3 (рис. 2.21). Проведите горизонтальную среднюю линию через центр окружности (рис. 2.22). Касательные к эллипсу в точках 2 и 4 определяют положение двух других сторон квадрата. Полученная таким образом фигура, ограниченная четырьмя касательными и есть описанный вокруг эллипса квадрат (рис. 2.23). Проверьте правильность построения квадрата при помощи диагоналей.

Вертикальный квадрат. Последовательность построения вертикального квадрата, описанного вокруг окружности, рассмотрим на примере, когда перед рисующим ставится задача описать вокруг горизонтального цилиндра четырехгранную призму, лежащую на горизонтальной плоскости. При таком положении цилиндра окружности его оснований будут вертикальными.

Начните построение с ближнего к вам основания. Описанный вокруг него квадрат имеет две вертикальные стороны, которые остаются вертикальными и на перспективном рисунке. Проведите две вертикальные касательные к эллипсу и найдите точки 2 и 4. Прямая, соединяющая их, будет иметь горизонтальное направление (рис. 2.24). Теперь проведите вертикальную прямую через центр окружности (точку, смещенную относительно центра эллипса дальше от зрителя) и найдите точки 1 и

3 (рис. 2.25). Прямые, касательные к эллипсу в этих точках, параллельны прямой 4 – 2, уходят с ней в одну точку схода на горизонте и определяют положение двух горизонтальных сторон квадрата (рис. 2.26). Второе основание призмы можно получить путем аналогичных построений. Соединив соответствующие вершины ближнего и дальнего оснований, завершите рисунок призмы, описанной вокруг цилиндра (рис. 2.27). Проверить правильность рисунка можно, проследив параллельность длинных сторон боковых граней призмы: они должны уходить в одну точку схода с осью цилиндра и его образующими.

Для закрепления этого материала подобные построения рекомендуется проделать несколько раз. Свободное владение этими навыками позволит вам перейти к перспективному изображению куба и других геометрических тел.

Содержание

Квадрат вписанный в окружность
Определение
Формулы
Радиус вписанной окружности в квадрат
Радиус описанной окружности около квадрата
Сторона квадрата
Площадь квадрата
Периметр квадрата
Диагональ квадрата
Соответствие круга и квадрата в перспективе.
🎬 Видео

Видео:Как построить квадрат, два способаСкачать

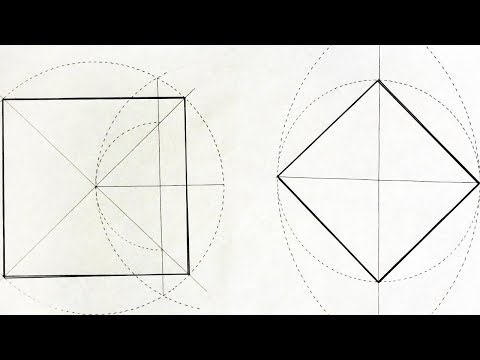
Квадрат вписанный в окружность

Видео:Найти площадь квадрата описанного около окружности радиуса 19Скачать

Определение

Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.

На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.

Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Формулы

Радиус вписанной окружности в квадрат

Радиус вписанной окружности в квадрат, если известна сторона:

Радиус вписанной окружности в квадрат, если известен периметр:

Радиус вписанной окружности в квадрат, если известна площадь:

Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:

Радиус вписанной окружности в квадрат, если известна диагональ:

Радиус описанной окружности около квадрата

Радиус описанной окружности около квадрата, если известна сторона:

Радиус описанной окружности около квадрата, если известен периметр:

Радиус описанной окружности около квадрата, если известнаплощадь:

Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:

Радиус описанной окружности около квадрата, если известнадиагональ:

Сторона квадрата

Сторона квадрата вписанного в окружность, если известнаплощадь:

Сторона квадрата вписанного в окружность, если известнадиагональ:

Сторона квадрата вписанного в окружность, если известен периметр:

Площадь квадрата

Площадь квадрата вписанного в окружность, если известна сторона:

Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:

Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:

Площадь квадрата вписанного в окружность, если известен периметр:

Площадь квадрата вписанного в окружность, если известна диагональ:

Периметр квадрата

Периметр квадрата вписанного в окружность, если известна сторона:

Периметр квадрата вписанного в окружность, если известна площадь:

Периметр квадрата вписанного в окружность, если известенрадиус вписанной окружности:

Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:

Периметр квадрата вписанного в окружность, если известна диагональ:

Диагональ квадрата

Диагональ квадрата вписанного в окружность, если известна сторона:

Диагональ квадрата вписанного в окружность, если известна площадь:

Диагональ квадрата вписанного в окружность, если известен периметр:

Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:

Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Соответствие круга и квадрата в перспективе.

Анализируя различные положения квадрата и окружности относительно точки зрения и линии горизонта а также правила их изображения в перспективе легко обнаружить общие закономерности. Геометрическая связь этих фигур определяется тем, что вокруг любой окружности можно описать квадрат, а также в любой квадрат можно вписать окружность.

Как вписать окружность в квадрат?

Рассмотрите рисунок 48. Квадрат и вписанная в него окружность имеют общий центр — точку пересечения диагоналей квадрата. Окружность касается сторон квадрата в точках 1,2,3,4.Точки касания делят стороны квадрата пополам. Для того чтобы изобразить вписанную в квадрат окружность (в перспективном рисунке — эллипс) необходимо определить положение осей эллипса и найти точки, задающие его размеры (точки 1 — 4).

Как построить квадрат описанный вокруг окружности

Горизонтальный квадрат.

Найдите точки касания на перспективном рисунке горизонтально расположенного квадрата (рис.49): для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода.

Окружность, лежащая в горизонтальной плоскости, изображается в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис.50). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1,2,3,4. Проверьте симметричность полученного эллипса относительно его осей (рис. 51).

Рис.50

перспективный рисунок простых геометрических тел

Вертикальный квадрат.

При вертикальном положении квадрата точки 1,2,3,4найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис.52). Несколько сложнее определить направление осей эллипса. Для решения этой задачи представьте, что изображаемый нами эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 53). Ось цилиндра всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Ее направление можно найти, опираясь на знание и опыт рисования куба, или взять с натуры, если таковая имеется. Таким образом, мы определили положение малой оси эллипса. А большая ось будет ей перпендикулярна и пройдет через точку, смещенную от пересечения диагоналей — центра окружности — ближе к зрителю (рис.54). На двух осях и по четырем точкам сначала наметьте эллипс легкими линиями, а затем уточните рисунок (рис.55).

Заметим, что эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и исправлений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним. Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе, поэтому задачу грамотного изображения квадрата современная методика рисования предлагает решать с помощью эллипса, вокруг которого описывается квадрат.