Как построить изометрическую проекцию треугольника (4 видео)

Как построить изометрию треугольника

Содержание

Черчение
Способы построения изометрической проекции плоских фигур, геометрических тел и деталей
СПОСОБЫ ПОСТРОЕНИЯ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ ПЛОСКИХ ФИГУР
ПОСТРОЕНИЕ ОСЕЙ ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ
ИЗОМЕТРИЧЕСКИЕ ПРОЕКЦИИ МНОГОУГОЛЬНИКОВ
Как построить изометрию треугольника
Как построить изометрическую проекцию треугольника
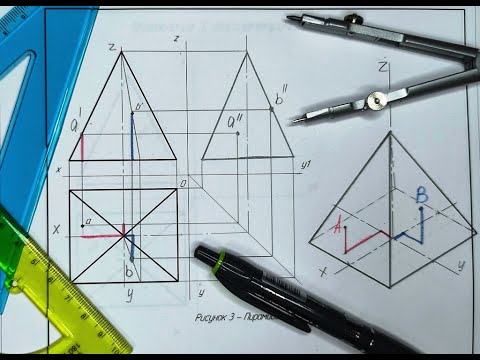
Практическая работа №5. Построение прямоугольной изометрической проекции группы геометрических тел и точек, принадлежащих поверхностям данных тел.
📽️ Видео

Видео:Построение изометрической проекциии треугольникаСкачать

Черчение

Видео:2 2 2 изометрия треугольника и шестиугольникаСкачать

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.

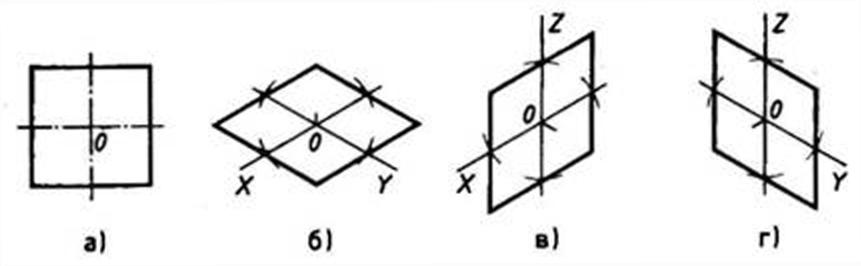
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.

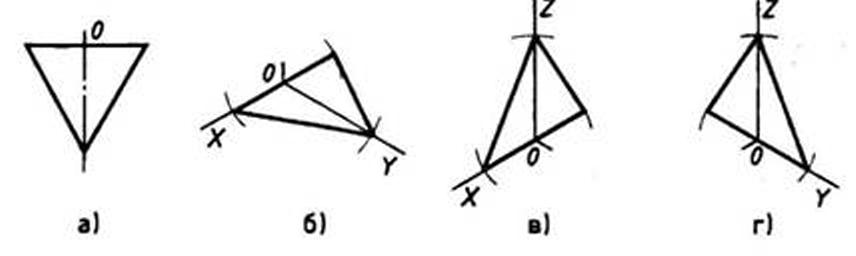
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

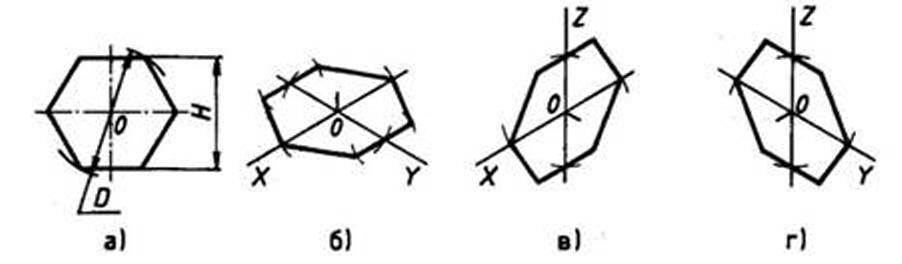
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

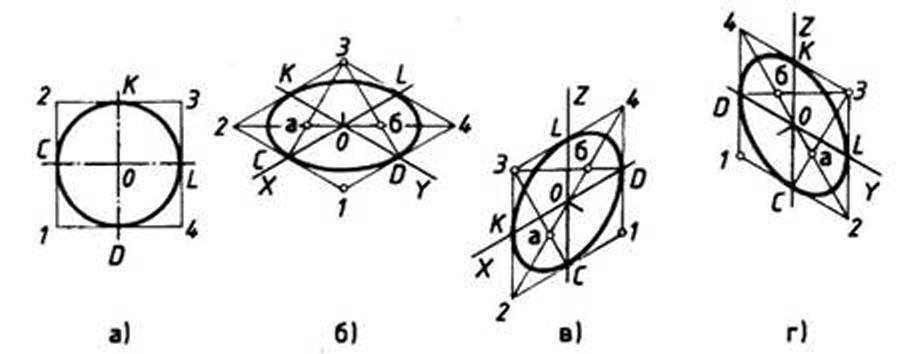
Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.

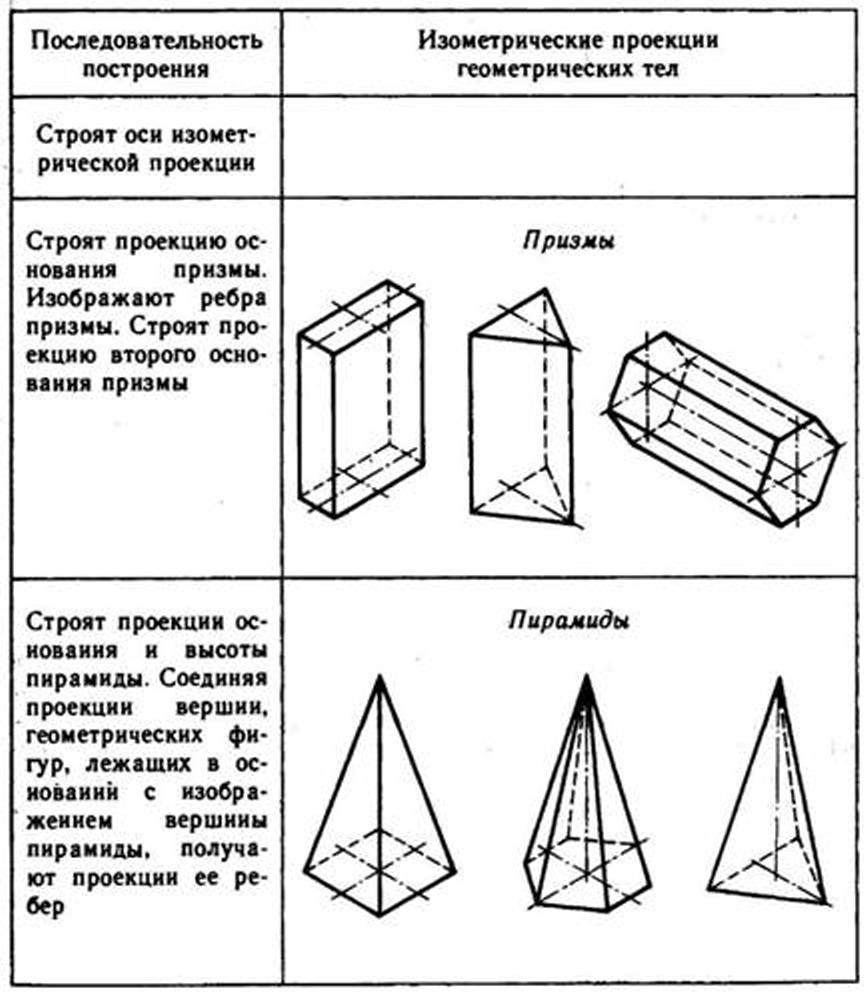
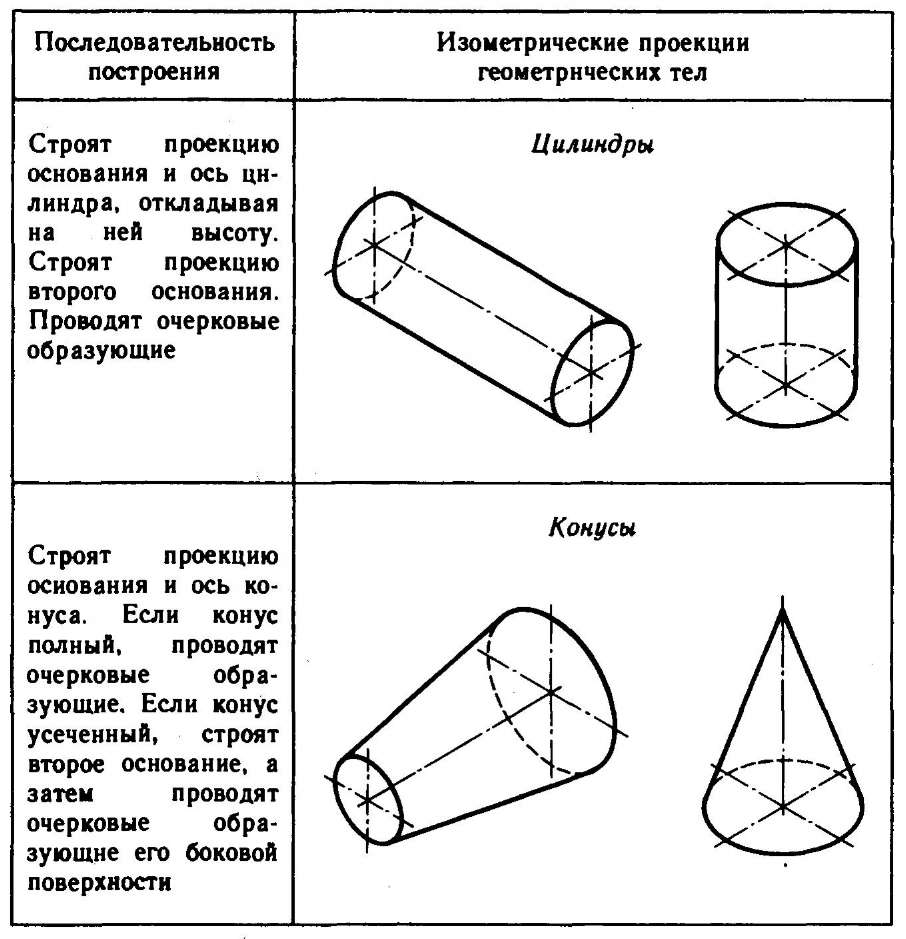
Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изображения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от формообразующей грани

4) обводка изометрической проекции (рис. 113).

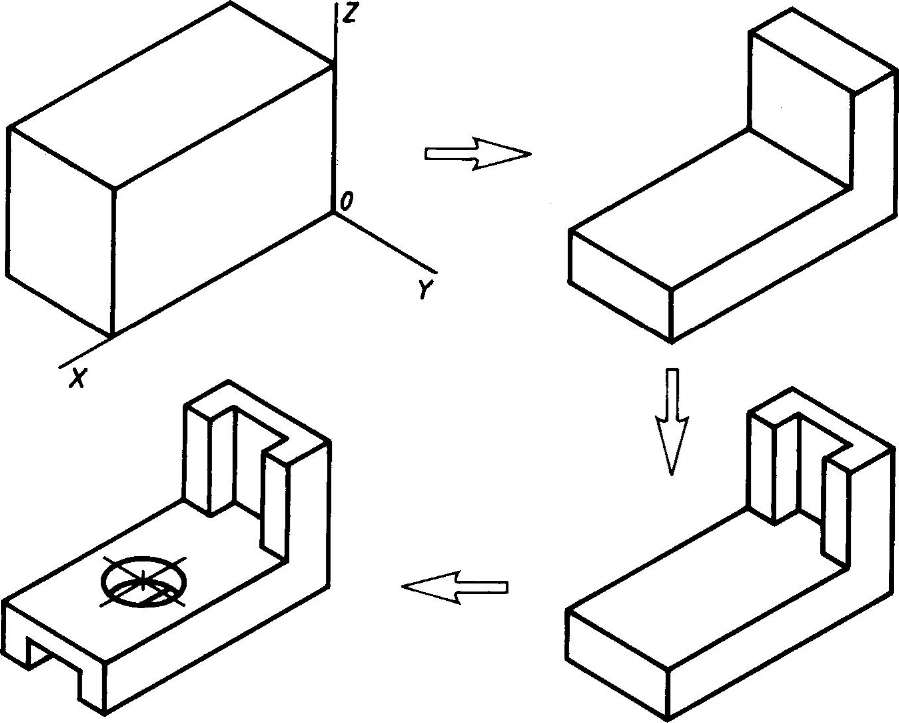
Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
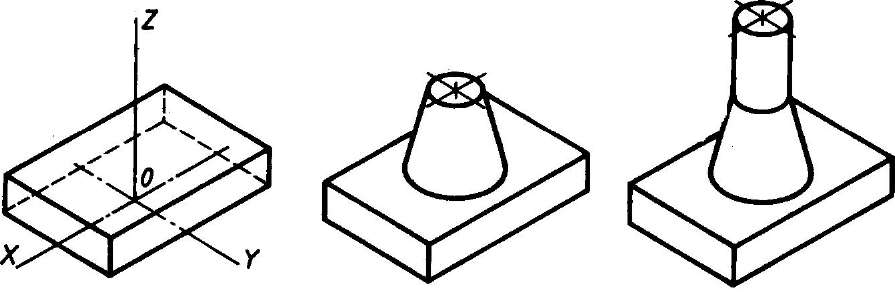
Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 115).
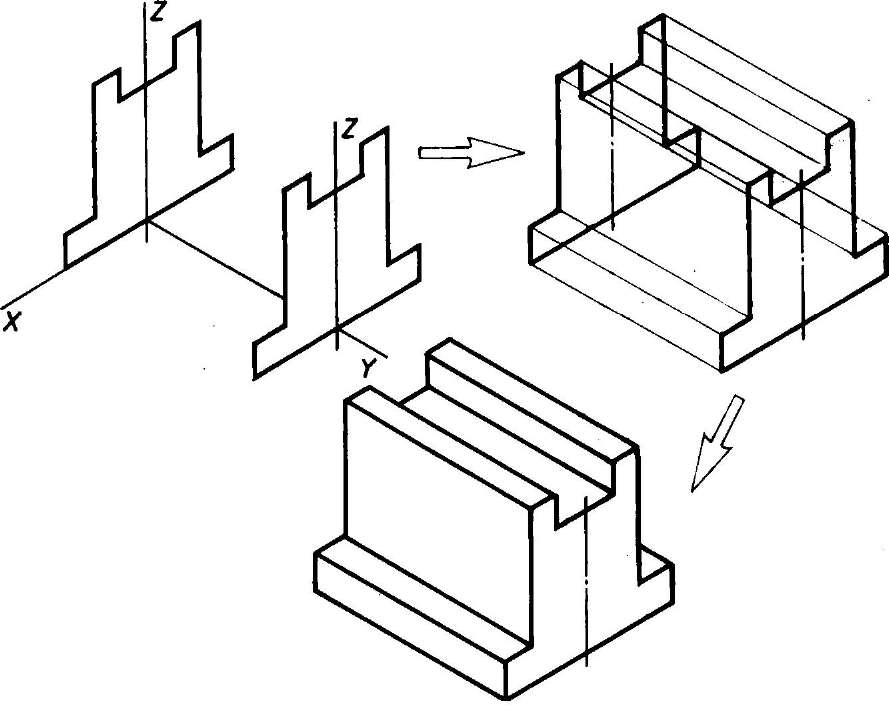
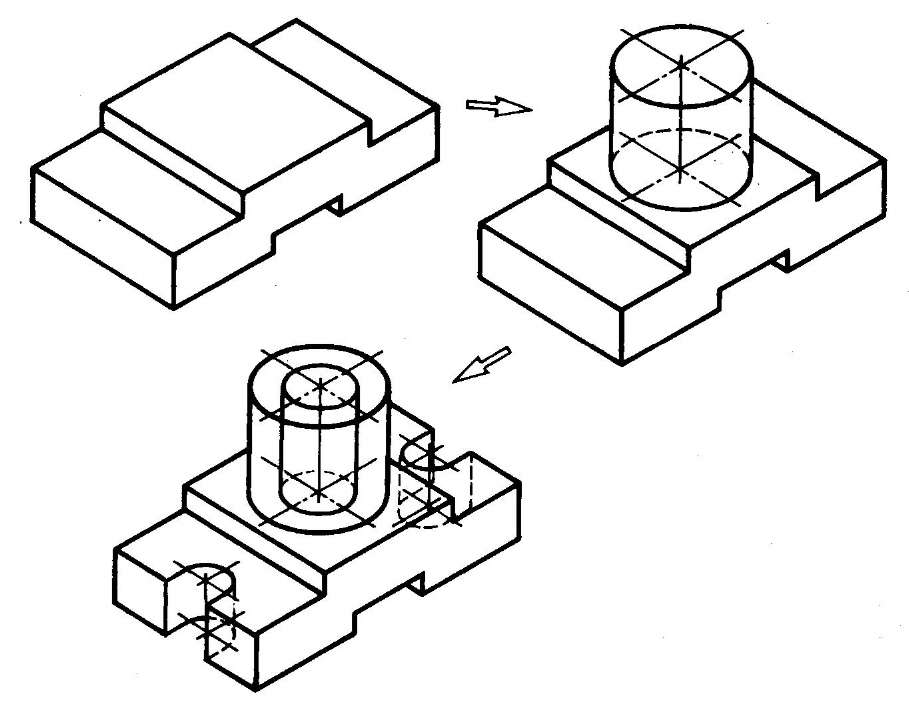
Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 116).

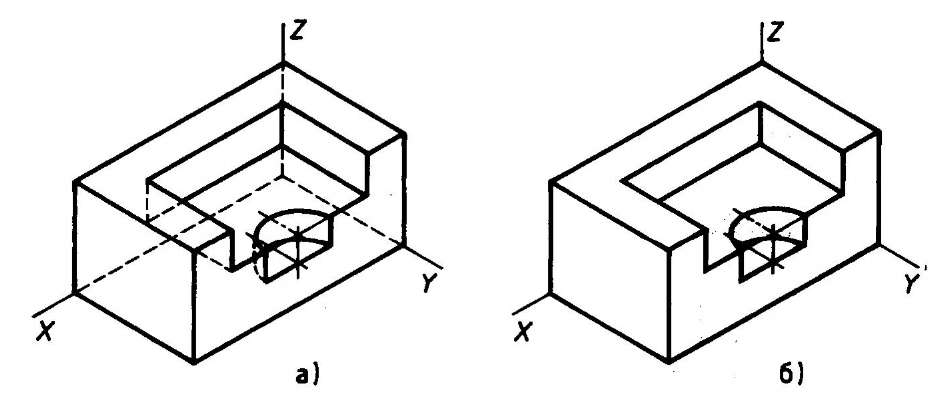
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) невидимых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Видео:Изометрическая проекция треугольникаСкачать

СПОСОБЫ ПОСТРОЕНИЯ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ ПЛОСКИХ ФИГУР

Видео:Лекция №2. Аксонометрические проекции. Виды аксонометрии. Стандартные аксонометрические проекции.Скачать

ПОСТРОЕНИЕ ОСЕЙ ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ

Как уже было рассмотрено, оси изометрической проекции располагаются под утлом 120° друг к другу.

Их можно построить несколькими способами.

А. С помощью циркуля. Первоначально проводят ось и выбирают на ней точку пересечения осей О. Из точки О любым радиусом проводят дугу, пересекающую ось в точке 1. Из нее тем же радиусом на дуге делают засечки в точках 3, 4, через которые и проводят оси (рис. 2.48).

Б. Построение осей с помощью линейки и угольника с углами 30°, 60° и 90° показано на рис. 2.49. Оси хиу проводят под углом 30° к горизонтальной прямой.

Видео:Аксонометрические проекции ТреугольникСкачать

ИЗОМЕТРИЧЕСКИЕ ПРОЕКЦИИ МНОГОУГОЛЬНИКОВ

Построение изометрической проекции предметов обычно начинают с изображения какой-то ее грани, в основе которой лежат плоские фигуры. Рассмотрим построение некоторых многоугольников по заданным прямоугольным проекциям.

Для всех построений первоначально проводят оси х и у на прямоугольных проекциях и соответствующие оси в изометрической проекции, т.е. производят увязку прямоугольных и аксонометрических осей.

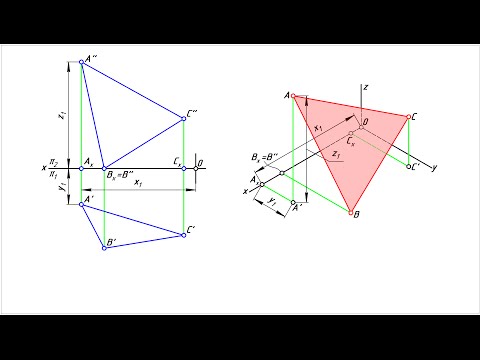
А. Построение треугольника, расположенного в горизонтальной плоскости (рис. 2.50). От точки О откладывают по оси х отрезки, равные половине стороны треугольника, а по оси у — его высоту И. Полученные точки соединяют отрезками прямых.

Аналогично строят треугольники, расположенные во фронтальной и профильной плоскостях (рис. 2.51).

Б. Построение квадрата, расположеного в горизонтальной плоскости (рис. 2.52). Вдоль оси х откладывают отрезок а, равный стороне квадрата, вдоль оси у — отрезок Ь, из полученных точек проводят отрезки, параллельные осям х и у.

В. Построение шестиугольника расположенного в горизонтальной плоскости (рис. 2.53).

Построение шестиугольников в плоскостях п₂ и п₃ показано на рис. 2.53, б.

Для построения шестиугольника оси изометрической проекции целесообразно выбрать так, чтобы они проходили через центр шестиугольника. По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки, равные половине расстояния h между противоположными сторонами.

От точек, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

При построении контуров сложных, несимметричных фигур (рис. 2.54) их вершины 7, 2, . 7 находят путем измерения на прямоугольной проекции разметок х_р х₂, х₃, х₄, х₅, и их переноса на осьх или прямые, параллельные этой оси изометрической проекции. Аналогично поступают и с размерами у_р у₂, у_у у₄. На пересечении соответствующих прямых находят вершины заданной плоской фигуры и соединяют их между собой.

Вопросы и задания

1. В какой последовательности в изометрической проекции выполняют построение треугольника? Любой плоской фигуры?
2. Из задачника выполните один из вариантов задания № 32. В нем необходимо построить изометрические проекции «плоских» фигур во фронтальной и профильной плоскостях проекций.

Видео:Черчение. 8 класс. Мазаева И.М. Изометрия и ДиметрияСкачать

Как построить изометрию треугольника

Раздел 2: Проецирование (6 часов)

Урок № 9: Рациональные построения в изометрии. Проекции плоских фигур и окружности

Ботвинников А.Д. § 7.2-7.3, 8 [1]

Степакова В. В. § 23 [3]
Вышнепольский И.С. § 13-14 [8]

В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.

1. Построение аксонометрической проекции квадрата показано на рис. 1, а и б.

Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.

Рис. 1. Аксонометрические проекции квадрата:

а — фронтальная диметрическая; б — изометрическая

2. Построение аксонометрической проекции треугольника показано на рис. 2, а и б.

Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у — его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.

Рис. 2. Аксонометрические проекции треугольника:

а — фронтальная диметрическая; б — изометрическая

3. Построение аксонометрической проекции правильного шестиугольника показано на рис. 3.

По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

Рис. 3. Аксонометрические проекции правильного шестиугольника:

а — фронтальная диметрическая; б — изометрическая

4. Построение аксонометрической проекции окружности .

Фронтальная диметрическая проекция удобна для изображения предметов с криволинейными очертаниями, подобных представленными на рис. 4.

Рис.4. Фронтальные диметрические проекции деталей

На рис. 5. дана фронтальная диметрическая проекция куба с вписанными в его грани окружностями. Окружности, расположенные на плоскостях, перпендикулярных к осям х и z, изображаются эллипсами. Передняя грань куба, перпендикулярная к оси у, проецируется без искажения, и окружность, расположенная на ней, изображается без искажения, т. е. описывается циркулем.

Рис.5. Фронтальные диметрические проекции окружностей, вписанных в грани куба

Построение фронтальной диметрической проекции плоской детали с цилиндрическим отверстием .

Фронтальную диметрическую проекцию плоской детали с цилиндрическим отверстием выполняют следующим образом.

1. Строят очертания передней грани детали, пользуясь циркулем (рис. 6, а).

2. Через центры окружности и дуг параллельно оси у проводят прямые, на которых откладывают половину толщины детали. Получают центры окружности и дуг, расположенных на задней поверхности детали (рис. 6, б). Из этих центров проводят окружность и дуги, радиусы которых должны быть равны радиусам окружности и дуг передней грани.

3. Проводят касательные к дугам. Удаляют лишние линии и обводят видимый контур (рис. 6, в).

Рис. 6. Построение фронтальной диметрической проекции детали с цилиндрическими элементами

Изометрические проекции окружностей .

Квадрат в изометрической проекции проецируется в ромб. Окружности, вписанные в квадраты, например, расположенные на гранях куба (рис. 7), в изометрической проекции изображаются эллипсами. На практике эллипсы заменяют овалами, которые вычерчивают четырьмя дугами окружностей.

Рис. 7. Изометрические проекции окружностей, вписанных в грани куба

Построение овала, вписанного в ромб.

1. Строят ромб со стороной, равной диаметру изображаемой окружности (рис. 8, а). Для этого через точку О проводят изометрические оси х и у, и на них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки a, b , с и d проводят прямые, параллельные осям; получают ромб. Большая ось овала располагается на большой диагонали ромба.

2. Вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги радиусом R, равным расстоянию от вершины тупого угла (точек А и В) до точек a, b или с, d соответственно. От точки В к точкам а и b проводят прямые (рис. 8, б); пересечение этих прямых с большей диагональю ромба дает точки С и D, которые будут центрами малых дуг; радиус R₁ малых дуг равен Са ( Db). Дугами этого радиуса сопрягают большие дуги овала.

Рис. 8. Построение овала в плоскости, перпендикулярной оси z.

Так строят овал, лежащий в плоскости, перпендикулярной к оси z (овал 1 на рис. 7). Овалы, находящиеся в плоскостях, перпендикулярных к осям х (овал 3) и у (овал 2), строят так же, как овал 1., только построение овала 3 ведут на осях у и z (рис. 9, а), а овала 2 (см. рис. 7) — на осях х и z (рис. 9, б).

Рис. 9. Построение овала в плоскостях, перпендикулярных осям х и у

Построение изометрической проекции детали с цилиндрическим отверстием .

Если на изометрической проекции детали нужно изобразить сквозное цилиндрическое отверстие, просверленное перпендикулярно передней грани, представленное на рисунке. 10, а.

Построения выполняет следующим образом.

1. Находят положение центра отверстия на передней грани детали. Через найденный центр проводят изометрические оси. (Для определения их направления удобно воспользоваться изображением куба на рис. 7.) На осях от центра откладывают отрезки, равные радиусу изображаемой окружности (рис. 10, а).

2. Строят ромб, сторона которого равна диаметру изображаемой окружности; проводят большую диагональ ромба (рис. 10, б).

3. Описывают большие дуги овала; находят центры для малых дуг (рис. 10, в).

4. Проводят малые дуги (рис. 10, г).

5. Строят такой же овал на задней грани детали и проводят касательные к обоим овалам (рис. 10, д).

Рис. 10. Построение изометрической проекции детали с цилиндрическим отверстием

Практические задания, тесты и домашние работы

Вопросы для повторения

pdf Вопросы

pdf

Видео:Построение треугольника в трёх проекцияхСкачать

Как построить изометрическую проекцию треугольника

Раздел 2: Проецирование (6 часов)

Урок № 9: Рациональные построения в изометрии. Проекции плоских фигур и окружности

Как построить изометрическую проекцию треугольника

Предыдущий урок

Поурочное планирование

Следующий урок

Ботвинников А.Д. § 7.2-7.3, 8 [1]

Степакова В. В. § 23 [3]
Вышнепольский И.С. § 13-14 [8]

1. Построение аксонометрической проекции квадрата показано на рис. 1, а и б.

Рис. 1. Аксонометрические проекции квадрата:

а — фронтальная диметрическая; б — изометрическая

2. Построение аксонометрической проекции треугольника показано на рис. 2, а и б.

Рис. 2. Аксонометрические проекции треугольника:

а — фронтальная диметрическая; б — изометрическая

3. Построение аксонометрической проекции правильного шестиугольника показано на рис. 3.

Рис. 3. Аксонометрические проекции правильного шестиугольника:

а — фронтальная диметрическая; б — изометрическая

4. Построение аксонометрической проекции окружности .

Рис.4. Фронтальные диметрические проекции деталей

Рис.5. Фронтальные диметрические проекции окружностей, вписанных в грани куба

Построение фронтальной диметрической проекции плоской детали с цилиндрическим отверстием .

1. Строят очертания передней грани детали, пользуясь циркулем (рис. 6, а).

3. Проводят касательные к дугам. Удаляют лишние линии и обводят видимый контур (рис. 6, в).

Рис. 6. Построение фронтальной диметрической проекции детали с цилиндрическими элементами

Изометрические проекции окружностей .

Рис. 7. Изометрические проекции окружностей, вписанных в грани куба

Построение овала, вписанного в ромб.

Рис. 8. Построение овала в плоскости, перпендикулярной оси z.

Рис. 9. Построение овала в плоскостях, перпендикулярных осям х и у

Построение изометрической проекции детали с цилиндрическим отверстием .

Построения выполняет следующим образом.

3. Описывают большие дуги овала; находят центры для малых дуг (рис. 10, в).

4. Проводят малые дуги (рис. 10, г).

5. Строят такой же овал на задней грани детали и проводят касательные к обоим овалам (рис. 10, д).

Рис. 10. Построение изометрической проекции детали с цилиндрическим отверстием

Практические задания, тесты и домашние работы

Вопросы для повторения

pdf Вопросы

pdf

Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Практическая работа №5. Построение прямоугольной изометрической проекции группы геометрических тел и точек, принадлежащих поверхностям данных тел.

Изучите теоретический материал

5.1. Общие сведения. Государственный стандарт устанавливает несколько видов аксонометрических проекций. Для построения

наиболее наглядных изображений применяется прямоугольная изометрическая проекция (кратко — изометрия, от греч изо — равный, одинаковый). Положение аксонометрических осей этой проекции приведено на рисунке 67, а. Как видно из чертежа, оси проекции в изометрии располагаются под углом 120° друг к другу. При построении фигур размеры отрезков по осям х 0 у 0 z 0 откладывают без изменения, т. е. действительные.

В том случае, когда действительные размеры берут только по двум осям (х0, z0), проекцию называют диметрической (от греч. ди — дважды).

Положение осей диметрической проекции дано на рисунке 67, б.

5.2. Аксонометрические проекции многоугольников. Построение аксонометрических проекций начинают с проведения осей. Параллельно им откладывают размеры отрезков.

Рассмотрим построение аксонометрических проекций плоских геометрических фигур, расположенных в горизонтальной плоскости. Построения даны в изометрической проекции.

Треугольник. Симметрично точке 00 (рис. 68) по оси х0 откладывают отрезки С0А0 и 00Е0, равные половине стороны треугольника, а по оси у0 — его высоту 00С0. Полученные точки А0, B0 и С0 соединяют отрезками прямых.

Квадрат. По оси х0 от точки 00 (рис. 69) откладывают отрезок а, равный стороне квадрата, вдоль оси у0 — также отрезок а. Затем проводят отрезки, параллельные отложенным.

Шестиугольник. По оси х0 вправо и влево от точки 00 (рис. 70) откладывают отрезки, равные стороне шестиугольника. По оси у0 симметрично точке 00 откладывают отрезки, равные половине расстояния L между противоположными сторонами шестиугольника, т. е. L/2

Через точки, полученные на оси у0, проводят вправо и влево параллельно оси х0отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

Если контур фигуры сложный, то при построении аксонометрической проекции эту фигуру удобно заключить в квадрат, прямоугольник и пр. (рис. 71).

5.3. Аксонометрическая проекция окружности. В аксонометрической проекции окружность в общем случае проецируется в кривую, которую называют эллипсом. Эллипс — замкнутая плоская кривая. Ее строят с помощью лекал. Поскольку строить эллипсы трудно, при изображении окружности в аксонометрии их разрешается заменять овалами. Овал — кривая, очерченная дугами окружности.

Рассмотрим построение овала, представляющего изометрическую проекцию окружности. Овал удобно строить, вписывая его в ромб, который является изометрической проекцией квадрата. Построение выполняют в следующем порядке:

Строят ромб, сторона которого равна диаметру изображаемой окружности. Для этого через точку 00 проводят оси х0 и у0 (рис. 72, а). На них от точки С0откладывают отрезки С01, С02 и т. д., равные радиусу изображаемой окружности. Через точки 1, 2, 3 и 4 проводят прямые, параллельные осям х0 и у0, получая на чертеже точки A, Б, С и D.

Для того чтобы вписать в ромб овал, из вершин тупых углов — точек В и А — проводят дуги. Их радиус R равен расстоянию от вершин тупых углов (точек Б и A) до точек 1, 2 или 3, 4 соответственно (рис. 72, б).