Как посчитать эксцентриситет окружности (5 видео)

окружность

Определение: Окружность — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром.

Если центр находится в начале координат, то окружность задается каноническим уравнением второй степени вида: х2+у2=R2 , где R — радиус окружности; х,у — текущие координаты точек, лежащих на окружности.

Для вывода данного уравнения возьмем на окружности произвольную точку М(х;у). Отрезок ОМ=R является гипотенузой в прямоугольном треугольнике ОМР, а катеты определяются координатами х и у точки М. Уравнение окружности получается по теореме Пифагора: х2+у2=R2, которое называется каноническим уравнением окружности с несмещенным центром.

Если центр окружности находится в точке С(х0;у0), то уравнение окружности со смещенным центром будет иметь

Построение окружности выполняется с помощью циркуля.

Содержание

эллипс
Эксцентриситет
Эксцентриситет орбиты
Определение эксцентриситета
Эксцентриситеты объектов Солнечной Системы
Эксцентриситеты в других системах
Похожие статьи
🎦 Видео

Видео:ЭллипсСкачать

эллипс

Определение: Эллипс — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная и равная большой оси эллипса.

Эллипс с несмещенным центром задается каноническим уравнением второй степени вида:

где а и в — полуоси, х,у — текущие координаты точек, лежащих на эллипсе. Центр симметрии находится в начале координат. Осями симметрии служат координатные оси.

При рассмотрении эллипса возможны два случая:

1. Если ав, то а называется большая полуось, лежащая на координатной оси Ох, а в — малая полуось, лежащая на координатной оси Оу;
2. Если ав, то а называется малая полуось, лежащая на координатной оси Ох, а в-большая полуось, лежащая на координатной оси Оу.

Фокусы F1 и F2 всегда лежат на большой оси эллипса, причем симметрично относительно центра симметрии на расстоянии:

где величина «с» определяет фокусное расстояние.

Для характеристики формы эллипса вводится эксцентриситет.

Определение: Эксцентриситетом эллипса называется отношение фокусного расстояния к длине его большой полуоси:

=, если ав и =, если ва.

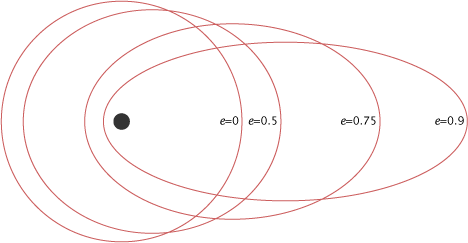
Значение эксцентриситета меняется в пределах 0??1. При этом форма эллипса изменяется от окружности (е=0, при а=в=R) и, вытягиваясь, вырождается в прямую (е=1, при а>>в).

Уравнение эллипса выводится из его основного свойства, представленного в определении. Возьмём на эллипсе произвольную точку М(х;у). Расстояния r1 и r2 от фокусов F1 и F2 до точки М(х;у) называются фокальными радиусами.

В соответствии с определением сумма фокальных радиусов есть величина постоянная, равная большой оси эллипса: r1 + r2 = 2а (при ав) — основное свойство эллипса. Для вывода уравнения эллипса необходимо выразить фокальные радиусы r1 и r2 через координаты точки М(х;у) и фокусов F1(с;0) и F2(-с;0)и подставить в это равенство.

Если центр симметрии смещен и находится в точке С(х0;у0), то уравнение эллипса со смещенным центром имеет вид:

Построение эллипса рассмотрим ниже на примерах.

Пример. Определить вид, параметры и построить линию, заданную уравнением:

Решение: 1. Это эллипс с несмещенным центром вида:

2. Найдем параметры: — большая полуось на оси Ох;

— малая полуось на оси Оу;

Фокусы F1(4.6;0) и F2(-4.6;0) лежат на большой оси, совпадающей с осью Ох, симметрично, на расстоянии с=4.6 относительно начала координат.

3. Построение эллипса (см. рисунок выше) выполним по этапам:
1) строим систему координат Оху;
2) на координатных осях симметрично относительно начала координат откладываем большую и малую полуоси (а=5, в=2) и показываем вершины эллипса А1,А2,В1,В2;
3) через вершины эллипса параллельно координатным осям строим осевой прямоугольник;
4) вписываем эллипс в осевой прямоугольник;
5) на большой оси, совпадающей с осью Ох, симметрично относительно начала координат показываем фокусы F1(4.6;0) и F2(-4.6;0).

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Эксцентриситет

Эксцентриситет – числовая степень отклонения от окружности. Узнайте, как выглядит эксцентриситет эллипса на схеме, уравнение, чему равен по формуле.

Если мы говорим о космосе, то эксцентриситет всегда относится к орбите или небесному телу. Он зависит от математического описания или же общей характеристики орбиты конкретного космического объекта, учитывая гравитацию Ньютона. Подобные орбиты приближаются к эллиптическим, а вот ключевой параметр, описывающий эллипс, именуют эксцентриситетом.

Если проще, то эксцентриситет круговой орбиты равен нулю, а радиальной или параболической – 1. Если показатель приравнивается к единице или превышает ее, то «орбиту» можно считать немного неправильной.

В системах, где присутствует больше одной планеты, орбитальные пути приближаются к форме эллипса, потому что каждый объект влияет на другой гравитационной силой и это определяет их совместные позиции (особенно примечательно для двоичных пульсаров).

Однако орбиты практически всегда достигают эллиптической формы, причем в вычислениях эксцентриситет эллипса все равно остается ключевым параметром. Почему? Просто это невероятно удобно, да и отклонение от эллипса объясняется малым возмущением.

Уравнение эксцентриситета с учетом гравитации Ньютона в системе с двумя компонентами очень проста. Если вы располагаете максимальной удаленностью тела от центра массы – ra (афелий для солнечных планет) и минимальной – rp (перигелий), то с расчетом не возникнет проблем:

Видео:§28 Эксцентриситет эллипсаСкачать

Эксцентриситет орбиты

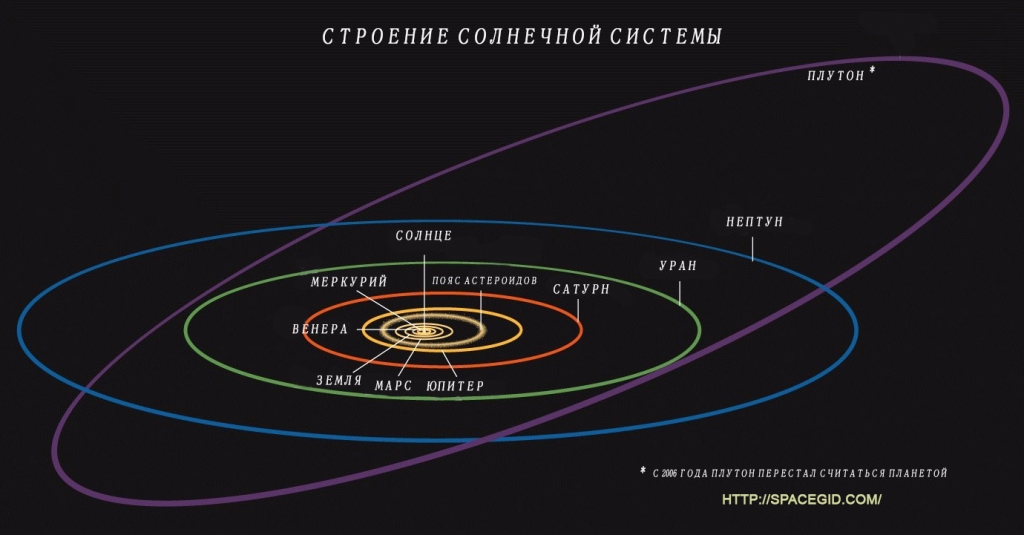
Строение Солнечной системы

Эксцентриситет (обозначается e или ε) входит в шестёрку кеплеровских элементов орбиты. Наряду с большой полуосью он определяют форму орбиты.

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Определение эксцентриситета

Первый закон Кеплера гласит о том, что орбиты любой планеты Солнечной системы представляет собой эллипс. Эксцентриситет определяет, насколько орбита отлична от окружности. Он равен отношению расстояния от центра эллипса (c) до его фокуса большой полуоси (a).

Видео:Радиус и диаметрСкачать

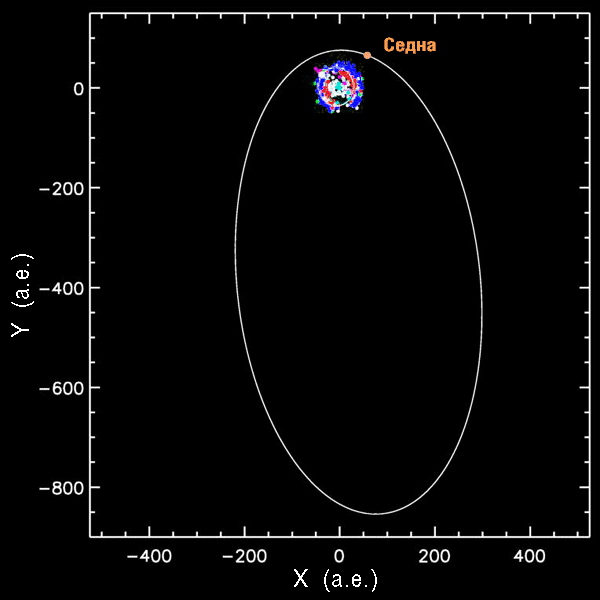
Эксцентриситеты объектов Солнечной Системы

Орбита Седны. В центре координат — Солнечная система, окруженная роем планет и известных объектов пояса Койпера.

В нашей системе орбиты планет ничем не примечательны. Самой «круговой» орбитой обладает Венера. Её афелий всего-лишь на 1,4 млн. км.больше перигелия, а эксцентриситет равен 0,007 (у Земли – 0,016). По довольно вытянутой орбите движется Плутон. Обладая ε = 0,244, он временами приближается к Солнцу даже ближе чем Нептун. Однако, поскольку Плутон не так давно попал в разряд карликовых планет, самую вытянутую орбит среди планет теперь имеет Меркурий, обладающий ε = 0,204.

Среди карликовых планет наиболее примечательна Седна. Обладая ε = 0,86, она делает полный оборот вокруг Солнца почти за 12 тысяч лет, удаляясь от неё в афелии более чем на тысячу астрономический единиц. Однако даже это несравнимо с параметрами орбит долгопериодических комет. Периоды их обращения порой исчисляются миллионами лет, а многих из них и вовсе никогда не вернутся к Солнцу – т.е. обладают эксцентриситетом, большем 1. Облако Оорта может содержать триллионы комет, удалённых от Солнца на 50-100 тысяч астрономических единиц (0,5 – 1 световых лет). На таких расстояниях на нихмогут влиять другие звёзды и галактические приливные силы. Поэтому такие кометы могут обладать очень непредсказуемыми и непостоянными орбитами с самими различными эксцентриситетами.

Наконец, самым интересным является то, что даже Солнце обладает совсем ни круговой орбитой, как это может показаться на первый взгляд. Как известно, Солнце движется вокруг центра Галактики, проделывая свой путь за 223 млн. лет. Причём, из-за бесчисленного взаимодействия со звездами она получила довольно ощутимый эксцентриситет, равный 0,36.

Видео:Длина окружности. Математика 6 класс.Скачать

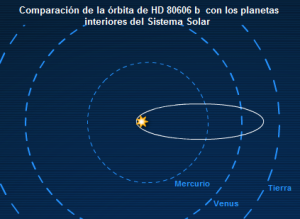
Эксцентриситеты в других системах

Сравнение орбиты HD 80606 b с внутренними планетами Солнечной системы

Открытие других солнечных систем неизбежно влечёт открытие планет с очень причудливыми параметрами орбит. Примером тому служат эксцентричные юпитеры, газовые гиганты с довольно высокими эксцентриситетами. В системах, имеющие такие планеты невозможно существование планет, подобных Земле. Они неизбежно упадут на гиганты или же статут их спутниками.
Среди обнаруженных на данный момент эксцентричных юпитеров самым большим эксцентриситетом обладает HD 80606b. Он движется вокруг звезды чуть меньшей, чем наше Солнце. Эта планета в перигелии приближается к звезде в 10 раз ближе, чем Меркурий к Солнцу, тогда как в афелии она удаляется от неё почти на астрономическую единицу. Таким образом, она имеет эксцентриситет 0,933.

Стоит отметить, что хоть данная планета и пересекает зону жизни, ни о каких видах привычной биосферы не может идти и речи. Её орбита создаёт на планете экстремальный климат.За короткий период сближения со звездой температура её атмосферы за считанные часы меняется на сотни градусов, в результате чего скорость ветров достигают многих километров в секунду. Подобными условиями обладают прочие планеты с высокими коэффициентами. Тот же Плутон, к примеру, при приближение к Солнцу приобретает обширную атмосферу, которая оседает в виде снега при удалении. В тоже время все Землеподобные планеты обладают орбитами, близкими к круговым. Поэтому эксцентриситет можно назвать одним из параметров, определяющим возможность наличия органической жизни на планете.