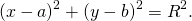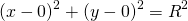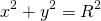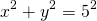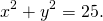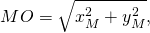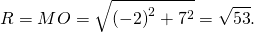Как понять проходит ли окружность через начало координат (7 видео)

Окружность с центром в начале координат

Чем окружность с центром в начале координат отличается от других окружностей?

Окружность с центром в точке (a;b) и радиусом R задаётся уравнением

Для окружности с центром в начале координат a=0, b=0:

Таким образом, уравнение окружности с центром в начале координат имеет вид

1) Написать уравнение окружности с центром в начале координат и радиусом 5.

В формулу уравнения окружности с центром в начале координат подставляем R=5:

2) Составить уравнение окружности с центром в начале координат, проходящей через точку M(-2;7).

Теперь запишем уравнение окружности с центром в точке O(0;0) и R=√53:

Содержание

Уравнение окружности.
Уравнение окружности
Перенос начала координат
📽️ Видео

Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:Уравнение окружности (1)Скачать

Уравнение окружности

Общее уравнение окружности записывается как:

Точка — центр окружности, R — её радиус.

Уравнение окружности радиуса R с центром в начале координат:

Уравнение окружности, проходящей через три точки (с помощью определителя) ,

Окружность также можно описать с помощью параметрического уравнения:

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

Если центр окружности совпадает с началом координат, функции принимают вид:

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Перенос начала координат

В аналитической геометрии основное значение имеет так называемая задача преобразования координат. Она заключается в следующем. Даны две системы координат (на плоскости или в пространстве) — «старая» и «новая». Требуется, зная координаты какой-нибудь точки или вектора в одной системе координат, найти координаты той же точки или вектора в другой системе.

Предположим, что даны две координатные системы, у которых одни и те же единичные векторы, но разные начала О и О’, так что новая система координат О’ получается из старой О, сдвигом на вектор ОО’ (рисунок представлен ниже).

При этом даны координаты точки О’ относительно системы О е₁ е₂ : О’ = (a, b). Мы уже знаем, что в этом случае координаты каждого вектора u в обеих системах одинаковы, потому что этими координатами являются координаты вектора u относительно одного и того же базиса, т.е. коэффициенты x, y в представлении

u = xe₁ + ye₂.

Посмотрим, как связаны между собою координаты x, y и x’, y’ произвольной точки М в обеих системах. Числа x, y суть координаты вектора ОМ (рисунок представлен ниже), а числа x’, y’- координаты вектора О’М (относительно того же базиса е₁ е₂). Но

Причем для вектора ОМ, ОО’, О’М (и базиса е₁ е₂) имеем

Так что векторное равенство (1) равносильно совокупности двух числовых равенств:

Эти формулы и решают поставленную задачу.

В случае плоскости вместо трех равенств (2) получаем два: если координаты нового начала О’ относительно старой системы координат суть a, b,так что O’ = (a, b) в старой системы координат, то координаты x, y произвольной точки М в старой системе выражаются через координаты той же точки в новой системе формулами:

Иногда при решении задач удобно вместо данной системы XOY использовать другую X’O’Y’, определенным образом ориентированную относительно данной системы.

Пусть новая система X’O’Y’ получена из старой ХОY параллельным переносом осей координат, т.е. оси новой системы параллельны осям старой и имеют одинаковое с ними направление (Рисунок представлен ниже). Пусть начало О’ новой системы имеет координаты (a, b) в старой системе.

Возьмем точку М на плоскости и найдем зависимость между ее координатами (х, у) в старой системе и (х’, у’) в новой. Из рисунка ясно, что

Если уравнение не содержит члена с произведением координат (В= 0), то с помощью параллельного переноса оно приводится к каноническому виду. Для этого необходимо в случае А ? 0, С ? 0 выделить полные квадраты для членов, содержащих у, и членов, содержащих х, затем для полученных полных квадратов вида (х — а) 2 , (y — b) 2 .