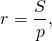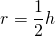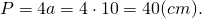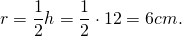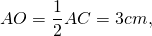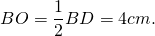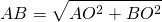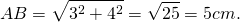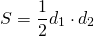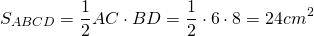Как параллелограмм можно вписать в окружность

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

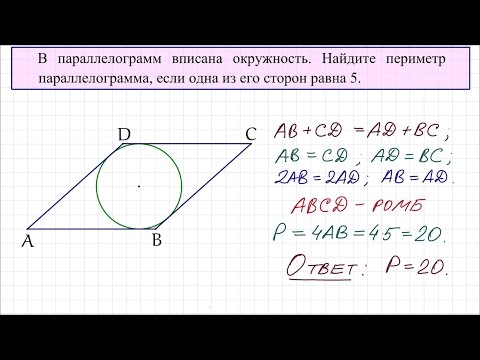
В параллелограмм вписана окружность

Если в условии задачи сказано, что в параллелограмм вписана окружность, то что сразу можно сказать об этом параллелограмме?

Для этого надо вспомнить, когда в четырехугольник можно вписать окружность. Это можно сделать лишь в том случае, если суммы противолежащих сторон четырехугольника равны.

Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).

Следовательно, если известно, что в параллелограмм можно вписать окружность, сразу можно сделать вывод, что все его стороны равны, и для него справедливы все свойства ромба. Если же дополнительно сказано, что хотя бы один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.

Радиус вписанной в ромб окружности можно найти по формуле

где S — площадь ромба, p — его полупериметр;

или как половину высоты ромба

1) В параллелограмм вписана окружность. Найти периметр параллелограмма, если одна из его сторон равна 10 см.

Из всех параллелограммов вписать окружность можно только в ромб (и квадрат). У ромба все стороны равны.

2) В параллелограмм вписана окружность. Найти её радиус, если высота параллелограмма равна 12 см.

Из параллелограммов вписать окружность можно в ромб (и квадрат). Радиус вписанной в ромб (и квадрат) окружности равен половине его высоты:

3) В параллелограмм вписана окружность. Найти её радиус, если диагонали параллелограмма равны 6 см и 8 см.

Из всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).

Пусть ABCD — ромб, AC=6 см, BD=8 см.

Рассмотрим треугольник AOB.

По теореме Пифагора

полупериметр — p=2a=2∙AB=25=10 см.

Следовательно, радиус вписанной окружности равен

Какой параллелограмм можно вписать окружность

Какой параллелограмм можно вписать окружность

Какие из данных утверждений верны? Запишите их номера.

1) Любой параллелограмм можно вписать в окружность.

2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.

Проверим каждое из утверждений.

1) «Любой параллелограмм можно вписать в окружность» — неверно, поскольку в окружность можно вписать только параллелограмм у которого сумма противоположных углов равна 180°.

2) «Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны» — верно, верно по признаку параллельности прямых.

3) «Точка пересечения двух окружностей равноудалена от центров этих окружностей» — неверно, поскольку эта точка удалена от каждой из окружностей на расстояние, равное их радиусам.

Всё о параллелограммах

Определение параллелограмма

С этой фигурой знакомы все, освоившие курс школьной программы. Впервые с понятием «параллелограмм» встречаются в 8 классе на уроках геометрии.

Параллелограмм — геометрическая фигура, являющаяся разновидностью четырехугольника. Противоположные стороны параллельны.

Стоит отметить, что всем известные фигуры, такие как квадрат, ромб, прямоугольник, являются параллелограммами. Исходя из этого, им можно дать следующие определения:

• Квадрат — параллелограмм с равными сторонами, пересекающимися под углом 90 градусов.
• Ромб — параллелограмм с равными между собой сторонами, не пересекающимися под углом 90 градусов.
• Прямоугольник — параллелограмм с неравными между собой сторонами, но пересекающимися под прямым углом.

Свойства параллелограмма

Для того чтобы определить параллелограмм, нужно обладать знанием о его свойствах. Рассмотрим их на примере четырехугольника MNPK.

• Длина противоположных сторон фигуры одинакова.

• Противоположные стороны параллельны.

• Углы, являющиеся противоположными, равны.

• Сумма всех четырех углов составляет 360 градусов.

∠NMK+∠NPK +∠MNP+∠MKP = 360°

• Сумма двух соседних углов равна 180 градусов.

• Диагонали разделяют параллелограмм на два треугольника, равные между собой.
• При пересечении диагоналей образуется точка пересечения, представляющая собой центр симметрии.
• Диагонали пересекаются и точка их пересечения разделяет каждую диагональ пополам.
• Биссектриса, проведенная из любого угла, отделает от четырехугольника равнобедренный треугольник.

Признаки параллелограмма

Четырехугольник MNPK можно называть параллелограммом при выполнении минимум одного условия:

1. Противоположные стороны равны парами: MK=NP, MN=PK.
2. Противоположные углы равны парами: ∠NMK=∠NPK, ∠MNP=∠MKP.
3. Диагонали пересекаются, и точка их пересечения разделяет каждую диагональ пополам.
4. Противоположные стороны равны и параллельны между собой: MK=NP, MN|PK.
5. Сумма квадратов двух диагоналей равняется сумме квадратов четырех его сторон: MP²+NK²=MN²+NP²+PK²+MK².

Теоремы параллелограмма

Все существующие теоремы доказывают свойства параллелограмма и исходят из определения о том, что это четырехугольник с противоположно расположенными параллельными сторонами.

Основные теоремы доказывают, что:

• параллелограммом является выпуклый четырехугольник;
• противоположные стороны попарно равны;
• углы, являющиеся противоположными, попарно равны;
• точка пересечения диагоналей разделает их пополам.

Параллелограммом является выпуклый четырехугольник

Многоугольник признается выпуклым при условии отсутствия продления до прямой хотя бы одной из сторон, а все оставшиеся стороны будут располагаться по одну сторону от этой прямой.

Пусть дан параллелограмм MNPK, сторона MN противоположна PK, а MK противоположна NP. Следовательно, исходя из определения, следует вывод о том, что MN || PK, а MK || NP.

Параллельные отрезки общих точек соприкосновения не имеют. Следовательно, PK находится со стороной MN по одну сторону. Отрезок NP соединяет точку N отрезка MN с точкой P отрезка PK. Противоположный отрезок MK соединяет оставшиеся две точки отрезков, что дает право утверждать о нахождении отрезков NP и MK по одну сторону от прямой MN. Исходя из всего вышесказанного, можно сделать вывод о том, что три стороны PK, NP и MK располагаются по одну сторону от отрезка MN.

Аналогичный алгоритм доказательства предположения о нахождении трех других сторон по одну сторону относительно остальных.

Противоположные стороны и углы попарно равны

Имеется четырехугольник MNPK, у которого MK=NP, MN=PK, ∠NMK=∠NPK, ∠MNP=∠MKP.

Параллелограмм — это, как мы знаем, четырехугольник. Следовательно, имеет 2 диагонали. Зная о том, что это выпуклая фигура, делаем вывод о делении фигуры на два треугольника. В нашем случае образовались треугольники MNP и MKP.

У треугольников имеется общее — сторона MP. ∠NPM=∠PMK, а ∠NMP=∠MPK, так как накрест лежащие углы, пересекая параллельные прямые, равны.

Следовательно, ΔMNP=ΔMKP, так как одна общая сторона и два равных смежных угла. Отсюда NP=MK, MN=PK.

∠NPM=∠PMK и ∠NMP=∠MPK

Из равенств следует, что ∠NMK=∠NPK.

Таким образом, теорема о равенстве противоположных углов и сторон доказана.

Точка пересечения диагоналей разделяет их пополам

Зная, что параллелограмм представляет собой выпуклый четырёхугольник, можно сказать о наличии двух пересекающихся диагоналей.

Есть четырехугольник MNPK с диагоналями NK и PM, пересекающимися в точке O. Возьмем два полученных треугольника MNO и PKO.

Из свойства противоположно лежащих сторон параллелограмма следует равенство MN=PK. Угол MNO и угол OKP — накрест лежащие, следовательно, они равны. Аналогично, два других угла — NMO и OPK — являются равными. Делаем вывод о равенстве треугольников MNO и PKO по стороне и двум углам.

Из рисунка видно, что углы MON и KOP вертикальные, а значит, они равны.

Зная о равенстве образовавшихся треугольников, можно утверждать и о равенстве всех соответствующих элементов. Сторона MO равна стороне PO, как и сторона NO=OK. Каждая из пар вместе представляет собой диагональ параллелограмма.

Таким образом, теорема о делении диагоналей пополам доказана.

Углы параллелограмма

Для углов действует правило, согласно которому смежные углы в сумме дают 180 градусов, а два противоположных равны друг другу. Основываясь на этих утверждениях, значения остальных углов находятся по формуле:

Свойства диагоналей параллелограмма

1. Точка пересечения диагоналей разделяет их пополам.
2. Любая диагональ разделяет фигуру на два треугольника, равные друг другу.
3. Сумма квадратов его диагоналей равняется сумме квадратов всех его сторон.
4. Площадь фигуры находится путем умножения длины диагоналей на синус угла, расположенного между ними, разделённый на 1/2.

Как вычислить площадь параллелограмма?

Существует несколько вариантов нахождения площади:

1. По основанию и высоте: S=a*h.
2. Зная значение двух смежных сторон и угла между ними: S=a*b*sin(α)°.
3. По длине диагоналей и углу между ними: S=1/2*d₁*d₂*sin α.

Разберем подробнее последнюю формулу площади на примере. Дан параллелограмм с диагоналями АС и BD. Точка пересечения — О. Угол пересечения диагоналей в точке O = 60°. Отрезки AO=6 см и OD=5 см Площадь находится по формуле:

Зная свойство деления диагоналей точкой пересечения пополам, получаем:

AC=AO*2=12 см и DB=OD*2=10 см

Подставляем полученные значения в формулу:

S=1/2 * 12*10*1/2√3=51,962 см 2

Как вписать параллелограмм в окружность?

Вписанный параллелограмм — это когда фигура находится внутри окружности.

Не каждый параллелограмм можно поместить внутрь окружности. Эту манипуляцию можно проделать с той фигурой, у которой два противоположных угла в сумме составляют 180 градусов.

Из этого можно прийти к выводу, что у вписанного в окружность параллелограмма все четыре угла равны 90°. Параллелограмм бывает трех видов: квадрат, ромб, прямоугольник. Следовательно вписать в окружность можно прямоугольник, квадрат.

1. Начертить окружность.
2. Найти ее центр, обозначить буквой O.
3. Выбрать любую точку на окружности и назвать ее точкой A.
4. Если вписываем квадрат, то нужно построить два диаметра с углом между ними в 90 градусов. Точки пересечения диагоналей с окружностью соединить прямыми линиями.
5. Для прямоугольника нужно иметь значения угла между диагоналями или размеры сторон. Зная размеры сторон по теореме Пифагора, высчитываем угол между диагоналями. Проведя один диаметр, обозначить точки пересечения с окружностью. От точки O (центр окружности и середина диагонали) отмерить угол между диагоналями. Провести второй диаметр через центр и новую полученную точку. Соединить полученные точки прямыми.

Как вписать окружность в параллелограмм?

В окружность можно вписать параллелограмм при условии равнозначных сумм противолежащих сторон. Из трех вариантов параллелограмма сумма противоположных сторон одинакова только у ромба. Следовательно, если в параллелограмм вписана окружность, то этот параллелограмм является ромбом.

1. Начертить ромб можно, зная длину минимум одной стороны и одного угла.
2. Провести горизонтальную линию, равную длине стороны.
3. Транспортиром отмерить известный угол и провести луч.
4. На луче отмерить тот же самый размер стороны.
5. Оставшиеся две стороны нарисовать параллельно имеющимся.
6. Согласно свойству ромба и вписанной окружности, проводим две биссектрисы из смежных углов (они же диагонали в ромбе).
7. Пересечение биссектрис отметить точкой О.
8. Точка О будет центром окружности.
9. Вписанная окружность должна касаться всех сторон параллелограмма. Следовательно, стороны ромба будут касательными к окружности.
10. Касательные перпендикулярны радиусу, который проходит к точке касания. Таким образом, из центра окружности (точки О) надо опустить перпендикуляр к любой стороне ромба.
11. Иголку циркуля поставить в точку О, а ножку — на точку касания перпендикуляра со стороной ромба.
12. Начертить окружность.
13. Правильно начерченная фигура будет соприкасаться со всеми сторонами ромба.

Как начертить параллелограмм?

Рассмотрим схему построения каждого вида по отдельности.

Алгоритм построения квадрата

1. Узнать размер одной стороны. Этого достаточно, так как все стороны в квадрате равны.
2. Один из признаков квадрата — все углы равны 90 градусов.
3. Чертим прямую, равную длине одной стороны.
4. С каждой стороны проводим перпендикулярную линию.
5. На перпендикулярах отмечаем нужную длину и ставим точку.
6. Соединяем две точки, построенные на перпендикулярных прямых.

Построение ромба

1. Начертить ромб можно, зная длину минимум одной стороны и одного угла.
2. Провести горизонтальную линию, равную длине стороны.
3. Транспортиром отмерить известный угол и провести луч.
4. На луче отмерить тот же самый размер стороны.
5. Оставшиеся две стороны нарисовать параллельно имеющимся.

Как построить прямоугольник

1. Нужно знать значения длины и ширины.
2. Начертить прямую, равную длине.
3. Провести два перпендикуляра с обеих сторон отрезка.
4. Отметить на перпендикулярных линиях отрезок равный ширине прямоугольника.
5. Соединить полученные два отрезка.
6. При правильном построении полученная линия должны быть перпендикулярна длине (первой начерченной линии).

Трапеция — это параллелограмм?

Обе фигуры являются четырехугольниками с двумя противоположными сторонами, которые равны. Трапеция по определению имеет 2 непараллельные стороны. В параллелограмме все 4 стороны попарно параллельны.

Таким образом, трапеция не является параллелограммом.

Средняя линия параллелограмма

Под этим термином понимается отрезок, соединяющий середины противоположных сторон параллелограмма.

Средняя линия всегда равна параллельной ей стороне

Свойства средней линии в параллелограмме:

• точка пересечения диагоналей является точкой пересечения средних линий;
• точка пересечения делит средние линии пополам;
• точка пересечения выступает центром симметрии параллелограмма.

Параллелограмм, у которого все стороны равны

Все четыре стороны имеют равное значение в двух разновидностях фигуры — ромбе и квадрате.

Ось симметрии параллелограмма

Под осью симметрии понимается прямая, разделяющая фигуру на две зеркально равные фигуры.

В прямоугольнике осью симметрии являются прямые, которые проходят через середину противоположной стороны.

В ромбе оси симметрии представляют собой его 2 диагонали.

Квадрат, объединяя в себе две предыдущие фигуры, имеет 4 оси симметрии: 2 диагонали и 2 средние линии.

В параллелограмм вписана окружность

Если в условии задачи сказано, что в параллелограмм вписана окружность, то что сразу можно сказать об этом параллелограмме?

Для этого надо вспомнить, когда в четырехугольник можно вписать окружность. Это можно сделать лишь в том случае, если суммы противолежащих сторон четырехугольника равны.

Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).

Следовательно, если известно, что в параллелограмм можно вписать окружность, сразу можно сделать вывод, что все его стороны равны, и для него справедливы все свойства ромба. Если же дополнительно сказано, что хотя бы один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.

Радиус вписанной в ромб окружности можно найти по формуле

где S — площадь ромба, p — его полупериметр;

или как половину высоты ромба

1) В параллелограмм вписана окружность. Найти периметр параллелограмма, если одна из его сторон равна 10 см.

Из всех параллелограммов вписать окружность можно только в ромб (и квадрат). У ромба все стороны равны.

2) В параллелограмм вписана окружность. Найти её радиус, если высота параллелограмма равна 12 см.

Из параллелограммов вписать окружность можно в ромб (и квадрат). Радиус вписанной в ромб (и квадрат) окружности равен половине его высоты:

3) В параллелограмм вписана окружность. Найти её радиус, если диагонали параллелограмма равны 6 см и 8 см.

Из всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).

Пусть ABCD — ромб, AC=6 см, BD=8 см.

Рассмотрим треугольник AOB.

По теореме Пифагора

полупериметр — p=2a=2∙AB=25=10 см.

Следовательно, радиус вписанной окружности равен