Как определить масштаб треугольника

разносторонний треугольник Это трехсторонний многоугольник, где у каждого разные размеры или длины; по этой причине ему дается название лестница, что на латыни означает скалолазание.

Треугольники — это многоугольники, считающиеся простейшими в геометрии, потому что они образованы тремя сторонами, тремя углами и тремя вершинами. В случае разностороннего треугольника, поскольку он имеет все разные стороны, это означает, что его три угла также будут разными..

• 1 Характеристика разносторонних треугольников
  • 1.1 Компоненты
• 2 свойства
  • 2.1 Внутренние углы
  • 2.2 Сумма сторон
  • 2.3 Несовместимые стороны
  • 2.4 Неконгруэнтные углы
  • 2.5 Высота, медиана, биссектриса и биссектриса не совпадают
  • 2.6 Ортоцентр, барицентр, стимулятор и околицентр не совпадают
  • 2.7 Относительные высоты
• 3 Как рассчитать периметр?
• 4 Как рассчитать площадь?
• 5 Как рассчитать высоту?
• 6 Как рассчитать стороны?
• 7 упражнений
  • 7.1 Первое упражнение
  • 7.2 Второе упражнение
  • 7.3 Третье упражнение
• 8 ссылок

Видео:Масштабы в геодезии. Поперечный, линейный, численный. Как читать и как пользоваться.Скачать

Характеристики разносторонних треугольников

Масштабные треугольники являются простыми многоугольниками, потому что ни одна из их сторон или углов не имеет одинаковую меру, в отличие от равнобедренных и равносторонних треугольников..

Поскольку все его стороны и углы имеют разные измерения, эти треугольники считаются неправильными выпуклыми многоугольниками.

По амплитуде внутренних углов разносторонние треугольники классифицируются как:

• Шкала прямоугольник треугольник: все его стороны разные. Один из его углов прямой (90 или ) а остальные резкие и с разными мерами.
• Шкала тупого угла треугольника: все его стороны разные, и один из его углов тупой (> 90 или ).
• Шкала острого угла треугольника: все его стороны разные. Все его углы острые ( или ), с разными мерами.

Еще одной характеристикой разносторонних треугольников является то, что из-за несовместимости их сторон и углов они не имеют оси симметрии.

компоненты

Медиана: линия, которая выходит из средней точки одной стороны и достигает противоположной вершины. Три медианы совпадают в точке, называемой центроид или центроид.

Биссектриса: это луч, который делит каждый угол на два угла одинакового размера. Биссектрисы треугольника совпадают в точке, называемой incentro.

Посредник: это сегмент, перпендикулярный стороне треугольника, который начинается в середине этого. В треугольнике три медиатрицы, совпадающие в точке, называемой окружностью.

Высота: линия, идущая от вершины к противоположной стороне, а также эта линия перпендикулярна этой стороне. Все треугольники имеют три высоты, которые совпадают в точке, называемой ортоцентром.

Видео:Масштаб. Как найти масштаб карты. Как найти отрезок на карте или расстояние на местности #масштабСкачать

свойства

Масштабные треугольники определены или идентифицированы, потому что они имеют несколько свойств, которые их представляют, возникших из теорем, предложенных великими математиками. Это:

Внутренние углы

Сумма внутренних углов всегда равна 180 или .

Сумма сторон

Сумма мер двух сторон всегда должна быть больше меры третьей стороны, a + b> c.

Непоследовательные стороны

Все стороны разносторонних треугольников имеют разные размеры или длины; то есть они неуместны.

Несогласованные углы

Поскольку все стороны разностороннего треугольника различны, их углы также будут разными. Однако сумма внутренних углов всегда будет равна 180º, и в некоторых случаях один из ее углов может быть тупым или прямым, в то время как в других все его углы будут острыми.

Высота, медиана, биссектриса и биссектриса не совпадают

Как и любой другой треугольник, в составной части есть несколько отрезков прямых линий, составляющих его, например: высота, медиана, биссектриса и биссектриса..

Из-за особенностей его сторон, в этом типе треугольника ни одна из этих линий не будет совпадать в одной.

Ортоцентр, барицентр, стимулятор и центр окружности не совпадают

Поскольку высота, медиана, биссектриса и биссектриса представлены различными отрезками прямых линий, в разностороннем треугольнике точки встречи — ортоцентр, центроцентр, стимулятор и окрицентр — будут находиться в разных точках (они не совпадают).

В зависимости от того, является ли треугольник острым, прямоугольным или разносторонним, ортоцентр имеет разные местоположения:

а. Если треугольник острый, ортоцентр будет внутри треугольника.

б. Если треугольник является прямоугольником, ортоцентр будет совпадать с вершиной прямой стороны.

с. Если треугольник тупой, ортоцентр будет находиться снаружи треугольника..

Относительные высоты

Высоты относительно сторон.

В случае разностороннего треугольника эти высоты будут иметь разные измерения. Каждый треугольник имеет три относительных высоты и для их расчета используется формула Герона.

Видео:Находим масштабСкачать

Как рассчитать периметр?

Периметр многоугольника рассчитывается по сумме сторон.

Так как в этом случае разносторонний треугольник имеет все стороны с различной мерой, его периметр будет:

P = сторона a + сторона b + сторона c.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Как рассчитать площадь?

Площадь треугольников всегда рассчитывается по одной и той же формуле, умножая основание на высоту и деля на два:

Площадь = (база _* ч) ÷ 2

В некоторых случаях высота разностороннего треугольника неизвестна, но есть математическая формула, предложенная математиком Хероном, для расчета площади, зная измерение трех сторон треугольника..

• a, b и c, представляют стороны треугольника.
• sp, соответствует полупериметру треугольника, то есть половине периметра:

В случае, если у вас есть измерение только двух сторон треугольника и угла, который сформирован между ними, площадь может быть рассчитана путем применения тригонометрических соотношений. Итак, вы должны:

Площадь = (сторона _* ч) ÷ 2

Где высота (h) — произведение одной стороны на синус противоположного угла. Например, для каждой стороны площадь будет:

Видео:Масштабы чертежей. Какие виды масштабов чертежей существуютСкачать

Как рассчитать высоту?

Поскольку все стороны разностороннего треугольника различны, вычислить высоту с помощью теоремы Пифагора невозможно.

Из формулы Герона, которая основана на измерениях трех сторон треугольника, можно вычислить площадь.

Высота может быть очищена от общей формулы площади:

Сторона заменяется измерением стороны a, b или c.

Другой способ вычислить высоту, когда известно значение одного из углов, состоит в применении тригонометрических соотношений, где высота будет представлять ногу треугольника..

Например, когда известен противоположный угол к высоте, он будет определяться синусом:

Видео:Масштаб. 6 класс.Скачать

Как рассчитать стороны?

Если у вас есть мера двух сторон и угол, противоположный этим, можно определить третью сторону, применив теорему косинусов.

Например, в треугольнике AB показана высота относительно сегмента AC. Таким образом, треугольник делится на два прямоугольных треугольника.

Для вычисления c-стороны (отрезок AB) применяется теорема Пифагора для каждого треугольника:

• Для синего треугольника вы должны:

Поскольку m = b — n, оно заменяется:

с 2 = ч 2 + б 2 (б — н) 2

с 2 = ч 2 + б 2 — 2 млрд + н 2 .

• Для розового треугольника вы должны:

час 2 = а 2 — N 2

Он заменяется в предыдущем уравнении:

с 2 = а 2 — N 2 + б 2 — 2 млрд + н 2

с 2 = а 2 + б 2 — 2BN.

Зная, что п = а _* cos C, заменяется в предыдущем уравнении, и получается значение стороны c:

с 2 = а 2 + б 2 — 2b_* в _* потому что C.

По закону косинусов стороны могут быть рассчитаны как:

• в 2 = б 2 + с 2 — 2b_* с _* потому что.
• б 2 = а 2 + с 2 — 2-й_* с _* потому что B.
• с 2 = а 2 + б 2 — 2b_* в _* потому что C.

Есть случаи, когда размеры сторон треугольника неизвестны, но их высота и углы, которые образуются в вершинах. Для определения площади в этих случаях необходимо применять тригонометрические соотношения.

Зная угол одной из его вершин, ноги идентифицируются и используется соответствующее тригонометрическое соотношение:

Например, катет AB будет противоположен углу C, но прилегает к углу A. В зависимости от стороны или катета, соответствующих высоте, другая сторона очищается, чтобы получить значение этого.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

обучение

Первое упражнение

Рассчитайте площадь и высоту разностороннего треугольника ABC, зная, что его стороны:

решение

В качестве данных приведены измерения трех сторон разностороннего треугольника.

Поскольку у вас нет значения высоты, вы можете определить площадь, применяя формулу Герона..

Сначала рассчитывается полупериметр:

sp = (8 см + 12 см + 16 см) ÷ 2

Теперь значения в формуле Герона заменены:

Зная площадь, можно рассчитать относительную высоту на стороне b. Из общей формулы, очистив ее, вы получите:

Площадь = (сторона _* ч) ÷ 2

46, 47 см 2 = (12 см _* ч) ÷ 2

ч = (2 _* 46,47 см 2 ) ÷ 12 см

h = 92,94 см 2 ÷ 12 см

Второе упражнение

Учитывая разносторонний треугольник ABC, меры которого:

• Сегмент AB = 25 м.
• Сегмент БК = 15 м.

В вершине B образуется угол 50 °. Рассчитайте относительную высоту в сторону с, периметр и площадь этого треугольника.

решение

В этом случае у вас есть меры двух сторон. Для определения высоты необходимо рассчитать измерение третьей стороны.

Поскольку задан угол, противоположный заданным сторонам, можно применить закон косинусов для определения измерения стороны переменного тока (b):

б 2 = а 2 + с 2 — 2-й_*с _* потому что B

б = переменный ток.

б 2 = (225) + (625) — (750) _* 0,6427

б 2 = (225) + (625) — (482,025)

Поскольку у вас уже есть значение трех сторон, рассчитайте периметр этого треугольника:

P = сторона a + сторона b + сторона c

Р = 15 м + 25 м + 19, 18 м

Теперь можно определить площадь, применяя формулу Герона, но сначала необходимо рассчитать полупериметр:

Измерения сторон и полупериметра заменяются формулой Герона:

Наконец, зная площадь, можно рассчитать относительную высоту на стороне c. Из общей формулы, очистив ее, вы должны:

Площадь = (сторона _* ч) ÷ 2

143,63 м 2 = (25 м _* ч) ÷ 2

ч = (2 _* 143,63 м 2 ) ÷ 25 м

h = 287,3 м 2 ÷ 25 м

Третье упражнение

В разностороннем треугольнике ABC сторона b имеет размер 40 см, сторона c имеет размер 22 см, а в вершине A образуется угол 90 или . Рассчитайте площадь этого треугольника.

решение

В этом случае даны измерения двух сторон разностороннего треугольника ABC, а также угла, образованного в вершине A.

Для определения площади нет необходимости вычислять меру стороны а, поскольку через тригонометрические соотношения угол используется для ее нахождения.

Так как угол, противоположный высоте, известен, это будет определяться произведением с одной стороны и синусом угла.

Подставляя в формулу площади, вы должны:

Площадь = (40 см _* 22 см _* сен 90) ÷ 2

Площадь = (40 см _* 22 см _* 1) ÷ 2

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Измерение по картам площадей

Практическая работа 1.

Измерение по картам площадей.

В результате измерения площадей различных объектов по топографическим планам и картам можно определить площади соответствующих контуров на местности (точнее, на уровенной поверхности).

Масштаб площади равен численному масштабу плана или карты, возведенному во вторую степень.

Например: для карты масштаба 1 : 10 000 масштаб площадей будет (1 : 10 000)2, или 1 : 100 000 000.

Для практических целей удобнее пользоваться именованным масштабом, т. е. определить, какой площади местности соответствует 1см2, или 1 м2 на карте данного масштаба.

Например: на карте масштаба 1 : 25 000

в 1 см 250 м, в 1 см2 (250 м)2 — в 1 см2 62 500 м2;

в 1 мм 25 м, в 1 мм2 (25 м)2 — в 1 мм2 625 м2

1 км2 = 1000 000 м2

1 га = 100 00 м2

1 м2 = 100 00 см2

На картах площади обычно измеряются графическим способом или с помощью палетки.

1) Графический способ. Сущность его состоит в том, что площадь участка на карте разбивается на простейшие геометрические фигуры — прямоугольники, трапеции, треугольники и др. Затем геометрическим путем определяется их площадь (по формулам геометрии). Необходимые построения делаются при помощи угольника и линейки тонко заточенным карандашом. Площади отдельных фигур суммируются, переводят в масштаб площадей данной карты и получают площадь объекта, выраженную в м2, км2, га.

S треугольника = *а * h

S прямоугольника = а * в

S трапеции = * h

а) территория леса на карте масштаба 1 : 10 000 имеет прямоугольную форму, длина сторон 41 мм и 34 мм.

Определим площадь леса в гектарах.

Площадь прямоугольника 41 мм * 34 мм = 1394 мм2.

Согласна масштаба, в 1 см 100 м, в 1 мм 10 м,

в 1 мм2 (10 м)2 , следовательно в 1 мм2 100 м2.

Переводим площадь леса согласна масштаба карты:

Площадь леса = 1394 мм2 * 100 м2 = 139400 м2 = 13, 94 га

б) участок сада на карте масштаба 1 : 300 000 имеет форму квадрата (со стороной 2,4 см) и треугольника (основание 2,1 см, высота 1,5 см). Определим площадь объекта.

Площадь квадрата = (2,4 см)2 = 5,76 см2,

площадь треугольника = 0,5 * 2,1 *1,5 = 1,575 см2.

Общая площадь 5,76 см2 + 1,575 см2 = 7,335 см2.

В 1 см на карте 3 км на местности, таким образом в 1 см2 9 км2.

Площадь объекта: 7,335 см2 * 9 км2 = 66,015 км2.

Графическим способом можно определить площадь объекта и с криволинейными контурами. При этом объект разбивают на геометрические фигуры, предварительно спрямив границы с таким расчетом, чтобы сумма отсеченных участков и сумма избытков компенсировали друг друга.

Определите масштаб площади для карт следующих масштабов: 1 : 500; 1 : 200 000; 1 : 20; 1: 3 000; 1 : 6; 1 : 500 000.

Чему равна площадь объектов, если на карте масштаба 1 : 20 000 они равны: 20 мм2, 48 мм2, 5 см2, 12,8 см2.

Найти площадь объекта:

а) Территория леса на карте масштаба 1 : 10 000 имеет прямоугольную форму, длина сторон 47 мм и 54 мм. Определите площадь леса в (га);

б) Луг на карте масштаба 1 : 25 000 имеет форму трапеции с размерами: основания 3,2 мм, 2,4 мм, высота 1,5 мм. Определите площадь в (га);

в) Участок овощных культур имеет на плане масштаба 1: 500 форму трапеции со сторонами: высота 15 мм, верхнее основание 21,5 мм, нижнее основание 33,3 мм. Определить площадь (га).

2) Для определения площадей криволинейных контуров пользуются палеткой. Палетка представляет собой прозрачную пластинку (из мелинекса, стекла, пластмассы) или лист кальки с сеткой квадратов (со стороной 1-5 мм). Ее накладывают на соответствующий контур и подсчитывают целые квадраты, поместившиеся внутри него. Неполные квадраты, рассекаемые границами контура, комбинируют на глаз так, чтобы в сумме были целые квадраты. Число квадратов, полученное при подсчете, умножают на площадь одного квадрата, находят площадь объекта по палетке. Затем умножают на масштаб площади карты.

Например: Карта масштаба 1 : 100 000. На исследуемый объект (луг) накладывается палетка (со стороной квадратиков 2 мм).

— кол-во полный клеток = 12

— кол-во неполный клеток переводим в полные клетки = 6

— сумма всех клеток = 18

— площадь одного квадрата = 2 мм * 2 мм = 4 мм2

— площадь объекта по палетке = 18 клеток * 4 мм2 = 72 мм2

— масштаб площади карты: в 1 см 1000 м, в 1 мм 100 м, в 1 м2 100 00 м2.

— площадь объекта (луг) = 72 мм2 * 100 00м2 = 720 000м2 = 72 га.

Определите численный масштаб карты, если известно:

а) что 1 см2 на этой карте соответствует 100 га;

б) что 1 мм2 на этой карте соответствует 64 га.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Масштаб в математике

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Определение горизонтальных расстояний с помощью масштабовСкачать

Понятие масштаба

Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.

Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.

Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.

• Например, одна тысячная (1:1000) означает, что все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.

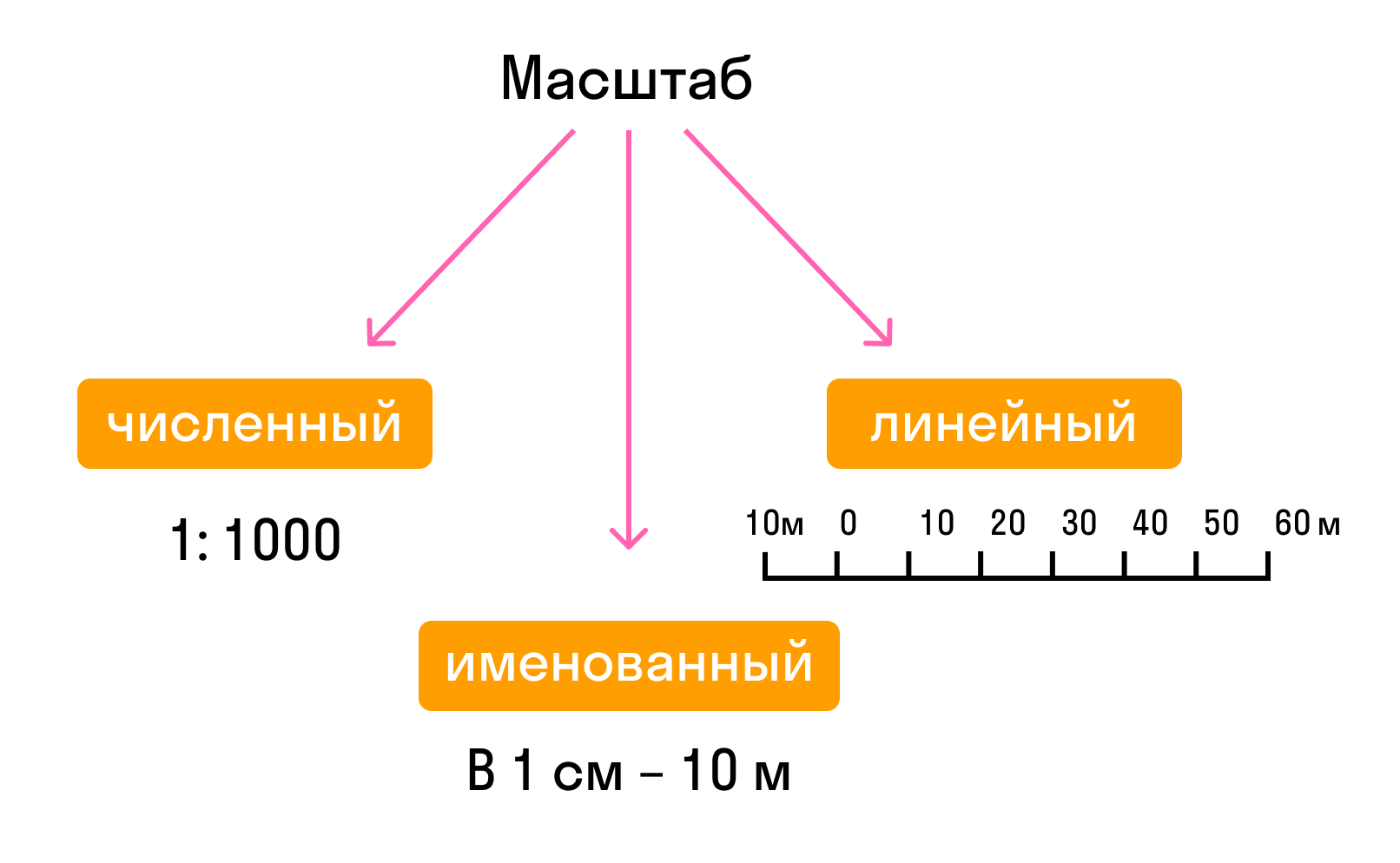
Масштаб бывает трех видов:

• численный, выражается в числах 1:1000;
• именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м — это величина масштаба;
• линейный, зная величину масштаба, можно определить расстояния.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение масштаба на карте

На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.

Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.

Масштаб — это отношение размера изображения к размеру изображаемого объекта.

Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.

На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.

Численные масштабы карт и соответствующие им масштабы на местности:

Масштаб 1 : 100 000

• 1 мм на карте — 100 м (0,1 км) на местности
• 1 см на карте — 1000 м (1 км) на местности
• 10 см на карте — 10000 м (10 км) на местности

Масштаб 1 : 10000

• 1 мм на карте — 10 м (0,01 км) на местности
• 1 см на карте — 100 м (0,1 км) на местности
• 10 см на карте — 1000 м (1 км) на местности

Масштаб 1 : 5000

• 1 мм на карте — 5 м (0,005 км) на местности
• 1 см на карте — 50 м (0,05 км) на местности
• 10 см на карте — 500 м (0,5 км) на местности

Масштаб 1 : 2000

• 1 мм на карте — 2 м (0,002 км) на местности
• 1 см на карте — 20 м (0,02 км) на местности
• 10 см на карте — 200 м (0,2 км) на местности

Масштаб 1 : 1000

• 1 мм на карте — 100 см (1 м) на местности
• 1 см на карте — 1000 см (10 м) на местности
• 10 см на карте — 100 м на местности

Масштаб 1 : 500

• 1 мм на карте — 50 см (0,5 метра) на местности
• 1 см на карте — 5 м на местности
• 10 см на карте — 50 м на местности

Масштаб 1 : 200

• 1 мм на карте — 0,2 м (20 см) на местности
• 1 см на карте — 2 м (200 см) на местности
• 10 см на карте — 20 м (0,2 км) на местности

Масштаб 1 : 100

• 1 мм на карте — 0,1 м (10 см) на местности
• 1 см на карте — 1 м (100 см) на местности
• 10 см на карте — 10м (0,01 км) на местности

Видео:определение масштаба карты при отсутствии поясняющих надписейСкачать

Решение задач на масштаб

Для закрепления темы решим несколько математических задач на масштаб за 6 класс.

Пример 1. Длина отрезка на карте равна 8 см. Найти длину соответствующего отрезка на местности, если масштаб карты равен 1 : 10 000.

8 см — это 1 часть

8 * 10 000 = 80 000 (см) — это 10 000 частей

80 000 см = 800 м

Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1:5000000.

400 км = 400 000 м = 40 000 000 см

40000000 : 5000000 = 40 : 5 = 8

Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить в виде отрезка длиной в 14 см?

🔍 Видео

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Масштаб карты. География 5 классСкачать

Военная топография определение масштаба картыСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

8 класс, 20 урок, Определение подобных треугольниковСкачать

Высоты треугольника.Скачать

Как найти площадь треугольника без формулы?Скачать