Как найти высоты тупоугольного треугольника

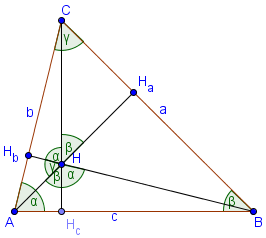
Расстояние между вершиной треугольника и противоположной стороной называется высотой. Формально, это самый короткий отрезок между вершиной треугольника и (с возможным продлением) противоположной стороной.

Каждый треугольник имеет 3 высоты которые пересекаются в одной точке — ортоцентре. Если мы используем стандартные обозначения, в треугольнике ABC , есть три высоты: AH_a, BH_b, CH_c . Эти три отрезка пересекаются в одной точке — ортоцентре (точка H на рисунке) треугольника. Для тупого треугольника (имеющего один угол, больше чем 90°), ортоцентр находится за пределами треугольника.

Высоты остроугольного треугольника

Ортоцентр — это точка внутри треугольника.

∠ AHB = 180 — γ = α + β
∠ BHC = 180 — α = β + γ
∠ AHC = 180 — β = α + γ
∠ AHH_c = β, ∠ BHH_c = α, ∠ BHH_a = γ

Высоты тупоугольного треугольника

Ортоцентр находится вне треугольнка.
Две высоты также всегда лежат вне треугольника.
∠ AHH_c = ∠ CBA = β
∠ H_cHB = ∠ CAB = α

Правый треугольник

Высота AH_a совпадает с AC.
Высота BH_b совпадает с BC.
Ортоцентр H совпадает с C.
∠ ACH_c = β, ∠ BCH_c =α

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Формулы

R — радиус описанной окружности
r — радиус вписанной окружности
p — полуперимерт: (a + b + c)/2

Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Видео:Высота в прямоугольном треугольнике. Как найти? Полезная формулаСкачать

Способы нахождения высоты треугольника: теорема и формула

Видео:Высота прямоугольного треугольникаСкачать

Определение высоты треугольника

Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.

Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.

Треугольники могут быть:

• разными по величине углов: прямоугольными, тупоугольными и остроугольными;
• разными по числу равных сторон: равносторонними, равнобедренными и разносторонними.

Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.

Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.

В геометрии высота треугольника обозначается буквой h.

В зависимости от типа треугольника высота может:

• падать на противоположную сторону — у остроугольного треугольника;
• находиться вне треугольника — у тупоугольного треугольника;
• совпадать с одной из сторон — у прямоугольного треугольника.

Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.

Для того чтобы определить графическое начертание высоты треугольника, необходимо:

1. Найти вершину фигуры.
2. Опустить вниз перпендикулярную линию к противоположной стороне.
3. Продлить противоположную сторону до пересечения с высотой, если требуется.

Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.

Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:

A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B

Выглядеть графически это будет так:

Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.

Через площадь и длину стороны, к которой опущена высота:

где S — уже известная площадь треугольника,

Через длины всех сторон:

h = 2 p p × a p × b p × c a

где a, b и c — стороны треугольника,

p — его полупериметр.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длину прилежащей стороны и синус угла:

s i n a — синус угла прилежащей стороны.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через стороны и радиус описанной окружности.

Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:

где b, c — стороны разностороннего треугольника, к которым не опущена высота,

R — радиус описанной окружности.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:

где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.

Данная формула подходит только для нахождения высоты прямоугольного треугольника.

Видео:Высота медиана биссектриса в тупоугольном треугольникеСкачать

Нахождение высоты равнобедренного треугольника через основание и боковые стороны

Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.

Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.

Формула для нахождения высоты в этом случае:

где a — основание,

b — равные боковые стороны.

Видео:Высоты треугольника.Скачать

Свойства высоты в равностороннем треугольнике

Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.

Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.

Высоту в таком треугольнике можно найти с помощью следующей формулы:

где а — сторона равностороннего треугольника.

Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:

а — сторона правильного равностороннего треугольника.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Нахождение высоты прямоугольного треугольника через его катеты

Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.

Важно отметить, что две другие высоты будут совпадать с катетами треугольника.

Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).

Причем гипотенуза также легко находится через катеты по теореме Пифагора:

Расчет высоты идет следующим образом:

где a, b и c — вышеупомянутые стороны треугольника.

🔍 Видео

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Построение высоты в треугольникеСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Точка пересечения высот треугольника.Скачать

Периметр треугольника. Как найти периметр треугольника?Скачать

КАК НАЙТИ ВЫСОТУ ПРОВЕДЕННУЮ К ГИПОТЕНУЗЕ??Скачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Теорема Пифагора для чайников)))Скачать

Катеты прямоугольного треугольника равны 3 и 4. Найдите высоту, проведённую к гипотенузеСкачать

№576. Высота прямоугольного треугольника, проведенная из вершины прямого угла, делитСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать