Основания равнобедренной трапеции равны 72 и 30. Радиус описанной окружности равен 39.
Найдите высоту трапеции.
Это задание ещё не решено, приводим решение прототипа.
Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Высота трапеции где KO и OH — высоты равнобедренных треугольников DOC и AOB. По теореме Пифагора:
Тогда
Если бы большее основание трапеции лежало выше центра окружности (то есть оба основания располагались по одну сторону от центра окружности) длина высоты равнялась бы не сумме, а разности найденных отрезков.
- Как найти высоту окружности трапеции
- Нахождение высоты трапеции: формулы и примеры задач
- Нахождение высоты трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
- Через диагонали и угол между ними
- Через площадь
- Примеры задач
- Трапеция. Формулы, признаки и свойства трапеции
- Основные свойства трапеции
- Сторона трапеции
- Формулы определения длин сторон трапеции:
- Средняя линия трапеции
- Формулы определения длины средней линии трапеции:
- Высота трапеции
- Формулы определения длины высоты трапеции:
- Диагонали трапеции
- Формулы определения длины диагоналей трапеции:
- Площадь трапеции
- Формулы определения площади трапеции:
- Периметр трапеции
- Формула определения периметра трапеции:
- Окружность описанная вокруг трапеции
- Формула определения радиуса описанной вокруг трапеции окружности:
- Окружность вписанная в трапецию
- Формула определения радиуса вписанной в трапецию окружности
- Другие отрезки разносторонней трапеции
- Формулы определения длин отрезков проходящих через трапецию:
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Решение №2085 Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Видео:Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать

Как найти высоту окружности трапеции
Видео:Радиус описанной окружности трапецииСкачать

Нахождение высоты трапеции: формулы и примеры задач
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Нахождение высоты трапеции
Через длины сторон
Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:
Через боковую сторону и прилежащий угол
Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
Через диагонали и угол между ними
Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b) /2.
Через площадь
Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Видео:ВЫСОТЫ ТРАПЕЦИИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:
Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см 2 . Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
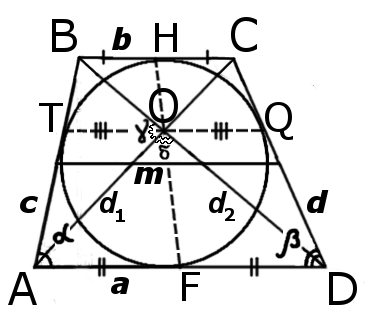 | 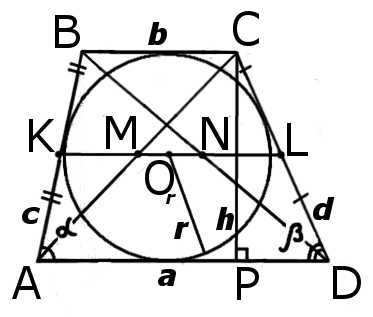 |
| Рис.1 | Рис.2 |
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Видео:Задача про трапецию, описанную около окружностиСкачать

Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Видео:ЕГЭ: Как найти высоту в равнобедренной трапеции, вписанной в круг. Матшкола 1 Ильвовского Д.М.Скачать
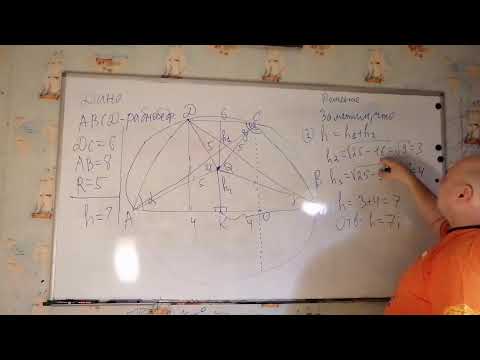
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Видео:Как найти стороны равнобокой трапеции, описанной около трёх попарно касающихся равных окружностей?Скачать
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) | a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
| S = | ( a + b ) | · h |
| 2 |
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Видео:Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Видео:Как найти высоту трапеции, зная все стороны?Скачать
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
| p = | a + c + d 1 |
| 2 |
a — большее основание
Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Видео:Найти высоту в трапеции вписанной в окружностьСкачать
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Please wait.
Видео:Задача.Высота трапеции, образованной касательными к двум окружностям.Скачать

We are checking your browser. mathvox.ru
Видео:Задание 24 Равнобокая трапеция Описанная окружностьСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:ОГЭ Задание 24 Трапеция Описанная и вписанная окружностиСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6ce343dacd591646 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:Высота равнобедренной трапеции, проведённая ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

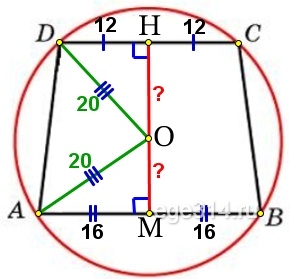
Решение №2085 Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Через центр окружности О проведём высоту НМ, она делит основания равнобедренной трапеции пополам:
DH = DC/2 = 24/2 = 12
АМ = АВ/2 = 32/2 = 16
Проведём радиусы DO и АО, получаем два прямоугольных треугольника ΔDHO и ΔAMO, найдём в них по теореме Пифагора катеты HO и МО соответственно:
Найдём высоту трапеции НМ:
НМ = НО + МО = 16 + 12 = 28