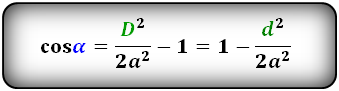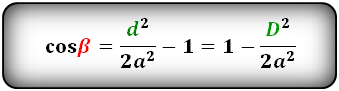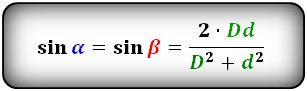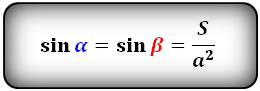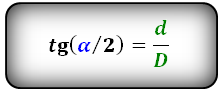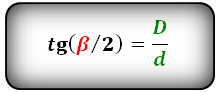С помощю этого онлайн калькулятора ромба можно найти углы ромба по известным элементам. Для нахождения углов ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Углы ромба через сторону и высоту
- 2. Углы ромба ромба через площадь и высоту
- 3. Углы ромба через площадь и сторону
- 4. Углы ромба через диагонали
- 5. Углы ромба через сторону и диагональ
- 6. Углы ромба через сторону и радиус вписанной окружности
- Радиус и угол ромба
- Свойства
- Как найти углы ромба вписанного в окружность
- Найти углы ромба
- Углы ромба онлайн
- 1. Углы ромба через сторону и высоту
- 2. Углы ромба ромба через площадь и высоту
- 3. Углы ромба через площадь и сторону
- 4. Углы ромба через диагонали
- 5. Углы ромба через сторону и диагональ
- 6. Углы ромба через сторону и радиус вписанной окружности
- Геометрические фигуры. Ромб. Углы ромба. Как найти угол ромба.
- Острый угол ромба равен 60 градусам.
- 🎦 Видео
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

1. Углы ромба через сторону и высоту
Пусть известны сторона и высота ромба (Рис.1).
 |
Покажем, что углы ромба через сторону и высоту вычисляются по формулам
| ( small alpha= mathrmfrac ) | (1) |
| ( small beta= 180°-alpha ) | (2) |
| (small frac=frac.) | (3) |
| (small sin alpha=frac) | (4) |
| (small alpha=mathrmfrac) | (5) |
Поскольку сумма соседних углов ромба равна 180° (свойство 4 статьи Ромб), то угол β вычисляется из формулы (2).
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

2. Углы ромба ромба через площадь и высоту
Рассмотрим ромб с высотой h и площадью S (Рис.2).
 |
Покажем, что углы ромба через площадь и высоту вычисляются по формулам:
| ( small alpha= mathrmfrac, ) | (6) |
| ( small beta= 180°-alpha . ) | (7) |
Площадь ромба через сторону и высоту вычисляется из формулы:
| ( small S=a cdot h. ) | (8) |
Найдем a из формулы (8) и подставим в (1):
| ( small alpha= mathrmfrac=mathrmfrac<large frac | (9) |
Как отметили в параграфе 1, соседний угол β вычисляется по формуле (7).
Видео:Задача 6 №27914 ЕГЭ по математике. Урок 132Скачать

3. Углы ромба через площадь и сторону
Пусть известны площадь и сторона ромба (Рис.3).
 |
Чтобы найти формулу углов ромба через площадь и сторону, из формулы (8) найдем h и подставим в (1):
| ( small alpha= mathrmfrac=mathrmfrac<large frac |
Следовательно угол α ромба через площадь и сторону вычисляется из формулы:
| ( small alpha =mathrmfrac. ) | (10) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

4. Углы ромба через диагонали
Пусть известны диагонали d1 и d2 ромба (Рис.4). Выведем формулу вычисления углов α и β ромба.
 |
| (small h=frac<large sqrt>.) | (11) |
| (small a=frac<large sqrt>.) | (12) |
Подставляя (11) и (12) в (4), получим:
| (small sin alpha=frac) ( small =frac<frac<large sqrt>><frac<large sqrt>> ) ( small =frac .) | (13) |
| (small alpha=mathrm frac .) | (14) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

5. Углы ромба через сторону и диагональ
Пусть известны сторона a=AB ромба и диагональ d=AC (Рис.5).
 |
Найдем углы ромба. Учитывая свойства 5, 6 и 7 ромба, получаем, что треугольник AOB прямоугольный и ( small angle ABO =frac .) Тогда для треугольника AOB имеют места следующие равненства:
| (small frac=sin frac,) |
| (small frac=cos frac) |
| (small sin frac=frac) | (15) |
| (small cos frac=frac.) | (16) |
Формулы половинного угла для синуса и косинуса имеют следующий вид:
| (small sin frac=±sqrt<frac>,) | (17) |
| (small cosfrac=±sqrt<frac>.) | (18) |
Найдем из формул (17),(18) ( small cos alpha ) и ( small cos beta: )
| (small cos alpha=1-2cdot sin^2 frac,) | (19) |
| (small cos beta=2cdot sin^2 frac-1,) | (20) |
Подставляя (15),(16) в (19),(20), получим формулы углов ромба через сторону и диагональ:
| (small cos alpha=1- frac,) | (21) |
| (small cos beta=frac-1.) | (22) |
| (small alpha=mathrm left(1- frac right),) | (23) |
| (small beta=mathrm left( frac-1 right).) | (24) |
Отметим, что полученный угол α находится напротив диагонали d, а угол β делится диагональю d на две равные части.
Видео:Углы, вписанные в окружность. 9 класс.Скачать

6. Углы ромба через сторону и радиус вписанной окружности
Пусть известны сторона ромба и радиус вписанной окружности (Рис.6). Найдем углы ромба.
 |
В статье Высота ромба мы вывели формулу высоты ромба через радиус вписанной октужности:
| (small h=2 cdot r.) | (25) |
Подставляя (25) в (4) и (5) параграфа 1 данной статьи, получим:
| (small sin alpha=frac) | (26) |
| (small alpha=mathrmfrac) | (27) |
Как отметили выше, соседний угол β ромба вычисляется по формуле:
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Радиус и угол ромба
Видео:Геометрия Один из углов ромба равен 60, а большая диагональ равна 24 см. Найдите радиус окружностиСкачать

Свойства
Радиус вписанной окружности, представляющий собой половину высоты, теоретически участвует в образовании прямоугольного треугольника, из которого можно найти сторону ромба, как отношение удвоенного радиуса к синусу угла α. a=2r/sin〖α 〗
Высота ромба будет равна удвоенному радиусу вписанной окружности. Площадь, ка произведение высоты и стороны ромба, через радиус вписанной окружности и угол α будет представлена произведением соответствующих выражений. Чтобы вычислить периметр, нужно будет эквивалент стороны умножить на четыре. h=2r S=(4r^2)/sin〖α 〗 P=8r/sin〖α 〗
Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Как найти углы ромба вписанного в окружность
Видео:Геометрия В ромб с острым углом 30 вписан круг, площадь которого равна Q. Найти площадь ромбаСкачать

Найти углы ромба
1. Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса углов через диагональ и сторону:
Формулы синуса углов через диагонали :
Формулы синуса углов через площадь S и сторону :
Формулы тангенса половинных углов через диагонали
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
Видео:№407. Найдите углы, которые образуют диагонали ромба с его сторонами, если одинСкачать

Углы ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти углы ромба по известным элементам. Для нахождения углов ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

1. Углы ромба через сторону и высоту
Пусть известны сторона и высота ромба (Рис.1).
 |
Покажем, что углы ромба через сторону и высоту вычисляются по формулам
| ( small alpha= mathrmfrac ) | (1) |
| ( small beta= 180°-alpha ) | (2) |
| (small frac =frac .) | (3) |
| (small sin alpha=frac ) | (4) |
| (small alpha=mathrmfrac ) | (5) |
Поскольку сумма соседних углов ромба равна 180° (свойство 4 статьи Ромб), то угол β вычисляется из формулы (2).
Видео:Площадь ромба. Легче понять...Скачать
2. Углы ромба ромба через площадь и высоту
Рассмотрим ромб с высотой h и площадью S (Рис.2).
 |
Покажем, что углы ромба через площадь и высоту вычисляются по формулам:
| ( small alpha= mathrmfrac , ) | (6) |
| ( small beta= 180°-alpha . ) | (7) |
Площадь ромба через сторону и высоту вычисляется из формулы:
| ( small S=a cdot h. ) | (8) |
Найдем a из формулы (8) и подставим в (1):
| ( small alpha= mathrmfrac =mathrmfrac > ) ( small =mathrmfrac ) | (9) |
Как отметили в параграфе 1, соседний угол β вычисляется по формуле (7).
Видео:Радиус описанной окружностиСкачать

3. Углы ромба через площадь и сторону
Пусть известны площадь и сторона ромба (Рис.3).
 |
Чтобы найти формулу углов ромба через площадь и сторону, из формулы (8) найдем h и подставим в (1):
| ( small alpha= mathrmfrac =mathrmfrac > ) ( small =mathrmfrac .) |
Следовательно угол α ромба через площадь и сторону вычисляется из формулы:
| ( small alpha =mathrmfrac . ) | (10) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
Видео:ЕГЭ Математика Задание 6#27913Скачать
4. Углы ромба через диагонали
Пусть известны диагонали d1 и d2 ромба (Рис.4). Выведем формулу вычисления углов α и β ромба.
 |
| (small h=frac >.) | (11) |
| (small a=frac > .) | (12) |
Подставляя (11) и (12) в (4), получим:
| (small sin alpha=frac ) ( small =frac >> > > ) ( small =frac .) | (13) |
| (small alpha=mathrm frac .) | (14) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
Видео:Геометрия, номера 45.1, 46.1 (радиус вписанной окружности)Скачать

5. Углы ромба через сторону и диагональ
Пусть известны сторона a=AB ромба и диагональ d=AC (Рис.5).
 |
Найдем углы ромба. Учитывая свойства 5, 6 и 7 ромба, получаем, что треугольник AOB прямоугольный и ( small angle ABO =frac .) Тогда для треугольника AOB имеют места следующие равненства:
| (small frac =sin frac ,) |
| (small frac =cos frac ) |
| (small sin frac =frac ) | (15) |
| (small cos frac =frac .) | (16) |
Формулы половинного угла для синуса и косинуса имеют следующий вид:
| (small sin frac =±sqrt >,) | (17) |
| (small cosfrac =±sqrt >.) | (18) |
Найдем из формул (17),(18) ( small cos alpha ) и ( small cos beta: )
| (small cos alpha=1-2cdot sin^2 frac ,) | (19) |
| (small cos beta=2cdot sin^2 frac -1,) | (20) |
Подставляя (15),(16) в (19),(20), получим формулы углов ромба через сторону и диагональ:
| (small cos alpha=1- frac ,) | (21) |
| (small cos beta=frac -1.) | (22) |
| (small alpha=mathrm left(1- frac right),) | (23) |
| (small beta=mathrm left( frac -1 right).) | (24) |
Отметим, что полученный угол α находится напротив диагонали d, а угол β делится диагональю d на две равные части.
Видео:Радиус вписанной в ромб окружности (6701)Скачать

6. Углы ромба через сторону и радиус вписанной окружности
Пусть известны сторона ромба и радиус вписанной окружности (Рис.6). Найдем углы ромба.
 |
В статье Высота ромба мы вывели формулу высоты ромба через радиус вписанной октужности:
| (small h=2 cdot r.) | (25) |
Подставляя (25) в (4) и (5) параграфа 1 данной статьи, получим:
| (small sin alpha=frac ) | (26) |
| (small alpha=mathrmfrac ) | (27) |
Как отметили выше, соседний угол β ромба вычисляется по формуле:
Видео:ЕГЭ ПЛАНИМЕТРИЯ РОМБА ВПИСАННОГО В ОКРУЖНОСТЬ | ЗОЛОТОЕ ПРАВИЛО РОМБА ЧЕРЕЗ ДИАГОНАЛИ | ГАРМАШУКСкачать

Геометрические фигуры. Ромб. Углы ромба. Как найти угол ромба.
Углы ромба, нахождение:
1. Сумма 4-х внутренних углов ромба равняется 360°, точно так же как и у всякого четырехугольника. Противоположные углы ромба имеют одинаковую величину, причем, всегда в 1-ой паре равных углов — углы острые, во второй — тупые. 2 угла, которые прилегают к 1-ной стороне в сумме составляют развернутый угол.
Ромбы с равным размером стороны могут внешне довольно сильно отличаться друг от друга. Это разница объясняется различной величиной внутренних углов. То есть, для определения угла ромба не хватит знать лишь длину его стороны.
2. Для вычисления величины углов ромба хватит знать длины диагоналей ромба. После построения диагоналей ромб разбивается на 4 треугольника. Диагонали ромба располагаются под прямым углом, то есть, треугольники, которые образовались, оказываются прямоугольными.
Ромб — симметричная фигура, его диагонали есть в одно время и осями симметрии, вот почему каждый внутренний треугольник равен остальным. Острые углы треугольников, которые образованы диагоналями ромба, равняются ½ искомых углов ромба.
3. Тангенс острого угла прямоугольного треугольника соответствует отношению противолежащего катета к прилежащему. ½ любой из диагоналей ромба оказывается катетом прямоугольного треугольника.
Обозначим большую и малую диагонали ромба как d₁ и d₂, а углы ромба — А (острый) и В (тупой), теперь из соотношения сторон в прямоугольных треугольниках внутри ромба находим:
4. Из формулы двойного угла tg (2α) = 2/(сtg α — tg α) находим тангенсы углов ромба:
По тригонометрическим таблицам находят углы, которые соответствуют полученным значениям тангенсов.
Видео:3 правила для вписанного четырехугольника #shortsСкачать

Острый угол ромба равен 60 градусам.
Когда острый угол ромба = 60°, значит, диагональ равняется стороне ромба и делит его на 2 одинаковых равносторонних треугольника.
∆ ABD и ∆ BCD — равносторонние,
1) Изучим треугольник ABD.
Т.к. AB=AD (так как являются сторонами ромба), значит, ∆ ABD является равнобедренным треугольником с основанием BD.
Углы при основании равнобедренного треугольника:
Так как каждый угол треугольника ABD равен 60 градусов, значит, ∆ ABD является равносторонним треугольником. Значит, BD=AB.
2) Треугольники ABD и BCD одинаковы по трем сторонам (AB=BC=CD=AD (как стороны ромба), BD=AB (из доказанного)).
То есть, ∆ BCD оказывается равносторонним треугольником.
Что и требовалось доказать.
Т.к. сумма углов ромба, которые прилежат к одной стороне, равна 180º, когда острый угол ромба равен 60º, его тупой угол равен 120º. Таким образом:
Когда тупой угол ромба равен 120 градусам, значит диагональ равняется стороне ромба и делит его на 2 равных равносторонних треугольника.
Ромб с прямыми углами называется квадратом.
🎦 Видео
Задание 17 ОГЭ по математике. Ромб. Найти высоту ромба.Скачать