Как найти центр треугольника разностороннего

Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.

Существует несколько понятий центра для треугольника.

Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.

Ортоцентр — точка пересечения его высот.

Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.

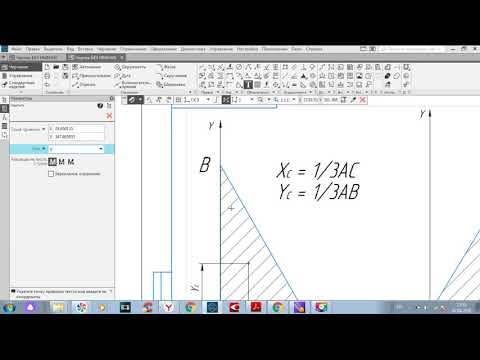
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).

Как найти центр треугольника

Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.

Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.

Центр равностороннего треугольника является также центром вписанной и описанной окружности.

Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.

Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:

• ввести в поле калькулятора координаты вершин треугольника;
• нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Площадь треугольника
Радиус описанной окружности

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

l = 2Rsin φ .

(1)

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α		sin β		sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

S =	a · b · с
	4R

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.