- Порядок определение центра
- Как найти центр окружности через хорду
- Определение хорды
- Свойства хорды к окружности
- Свойства хорды и вписанного угла
- Свойства хорды и центрального угла
- Формулы нахождения хорды
- Решение задач
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- 📸 Видео
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Порядок определение центра
Взаимное пересечение перпендикуляров, восставленных в середине каждой хорды, определяет центр окружности (точку О). На фиг. 9,6 показано нахождение центра дуги окружности (построение аналогично предыдущему).
Выпрямление дуги окружности
Определение длины 1 дуги АВ окружности (приближенный способ, фиг. 10).
Через хорду АВ проводят перпендикуляр (фиг. 10,а), пересекающий дугу в точке К. Из точек С и D, как из центров, радиусами г, равными d— диаметру окружности, проводят две дуги до взаимного их пересечения в точке 01.
Расстояние между точками пересечения лучей 01А и O1B с касательной, проведенной к окружности в точке К, определяет приближенное значение спрямленной дуги (отрезок А1В1).
Расстояние между точками С1 и D1 определяет приближенную длину полуокружности. При отсутствии центра окружности
длина дуги АВ (фиг. 10,6) может быть определена следующим путем: хорду А В делят на четыре равные части; одну четвертую часть откладывают от точки В на дуге АВ; полученную точку С соединяют с точкой деления 1. Отрезок 1—С равен половине длины дуги АВ; CD — приближенное значение длины всей дуги АВ.
Определение длины окружности. Длину окружности определяют по формуле l=П*D, где l — длина окружности, П = 3,14159, a D—диаметр окружности. На фиг. 11,а показана длина l окружности диаметра D.
Графически длина окружности приближенно может быть определена путем суммирования длины двух сторон аз равностороннего треугольника и двух сторон а квадрата, вписанных в окружность, как это показано на фиг. 11,6 (2аз + 2а4). Точность определения — 0,01. На фиг. 11,в длина окружности определена следующим способом: из центра О под углом 30° проводят прямую до пересечения ее в точке А с касательной к окружности; от точки А откладывают отрезок АВ, равный трем радиусам R; из точки В, как из центра, радиусом ВМ проводят дугу окружности до пересечения с касательной прямой в точках С и D. Отрезок CD будет равен длине окружности. Точность определения — 0,0001.
Определение приближенной длины очерка эллипса (фиг. 12). Для определения длины очерка эллипса ACBD соединяют точки А и С и из центра О радиусом, равным АС, засекают на осях эллипса точки М и N. Измерив длину отрезка MN, умножают ее на 3,14 и получают приближенную длину очерка эллипса (l = 3,14*MN).
Видео:Радиус Хорда ДиаметрСкачать

Как найти центр окружности через хорду
| Учебный курс | Решаем задачи по геометрии |
Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать  Определение хорды
Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности. Видео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Свойства хорды к окружности
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать  Свойства хорды и вписанного углаВидео:Радиус и диаметрСкачать  Свойства хорды и центрального углаВидео:Быстро и легко определяем центр любой окружностиСкачать  Формулы нахождения хорды
Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать  Решение задачПримечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.
Решение. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 Откуда
Решение. 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны: 90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ; Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать  Отрезки и прямые, связанные с окружностью. Теорема о бабочке
Видео:Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать  Отрезки и прямые, связанные с окружностью
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности Круг |  Конечная часть плоскости, ограниченная окружностью Радиус |  Отрезок, соединяющий центр окружности с любой точкой окружности Хорда |  Отрезок, соединяющий две любые точки окружности Диаметр |  Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности Касательная |  Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания Секущая |  Прямая, пересекающая окружность в двух точках Видео:4K Как найти центр окружности, how to find the center of a circleСкачать  Свойства хорд и дуг окружности
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. Диаметр, проходящий через середину хорды |  Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. Равные хорды |  Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. Хорды, равноудалённые от центра окружности |  Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. Две хорды разной длины |  Большая из двух хорд расположена ближе к центру окружности. Равные дуги |  У равных дуг равны и хорды. Параллельные хорды |  Дуги, заключённые между параллельными хордами, равны. Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать  Теоремы о длинах хорд, касательных и секущих
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Касательные, проведённые к окружности из одной точки | Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. Касательная и секущая, проведённые к окружности из одной точки | Секущие, проведённые из одной точки вне круга | Видео:Как найти центр кругаСкачать  Доказательства теорем о длинах хорд, касательных и секущихТеорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1). Тогда справедливо равенство Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство откуда и вытекает требуемое утверждение. Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2). Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство откуда и вытекает требуемое утверждение. Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3). Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство Доказательство . Проведём из точки A касательную AB к окружности (рис. 4). Точка B – точка касания. В силу теоремы 2 справедливы равенства откуда и вытекает требуемое утверждение. Видео:Деление окружности на 3; 6; 12 равных частейСкачать  Теорема о бабочкеТеорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны. Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения: Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим Воспользовавшись теоремой 1, получим Воспользовавшись равенствами (1) и (2), получим Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство откуда вытекает равенство что и завершает доказательство теоремы о бабочке. 📸 ВидеоВсё про углы в окружности. Геометрия | МатематикаСкачать  Геометрия Задача найти центр круга /math and magicСкачать  Найти центр и радиус окружностиСкачать  Демо ОГЭ по математике. Задание 17. Хорда окружности.Скачать  Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать 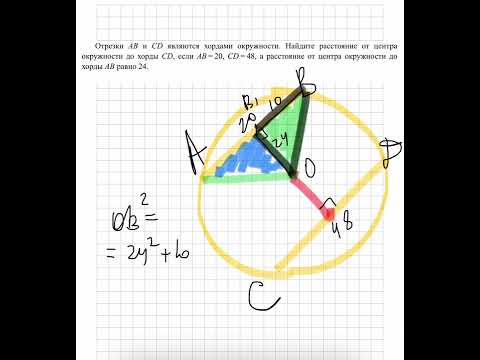 Окружность и круг, 6 классСкачать  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||











 Отрезки и прямые, связанные с окружностью
Отрезки и прямые, связанные с окружностью



































