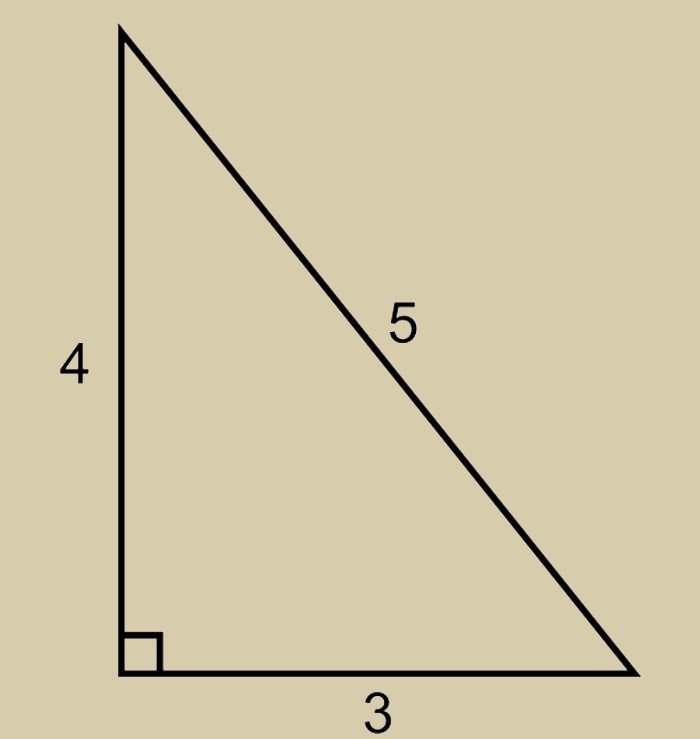
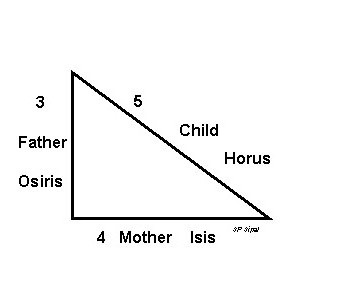
Египетский треугольник – прямоугольный треугольник с отношением сторон 3:4:5. Это наиболее простой из треугольников, стороны и площади которых выражаются целыми числами. Он представляет собой прекрасную иллюстрацию теоремы Пифагора – действительно, квадрат его гипотенузы (25) очевидно равен сумме квадратов его катетов (9 и 16). Предполагается даже, что именно знакомство с египетским треугольником сподвигло Пифагора на формулировку его теоремы. Впрочем, как всегда в подобных случаях, историки древности, которые не являются специалистами ни в одной другой области знания, кроме истории (и уж точно плохо смыслят в математике), могут ошибаться.
Так или иначе, имеются многочисленные указания на то, что теорема Пифагора вообще и египетский треугольник в частности были известны и широко использовались за много веков до Пифагора и далеко за пределами Египта – в Месопотамии, в долине Инда, в древнем Китае. И вправду, корень многих знаний следует искать, наверное, в практической деятельности человека. Как только возникла необходимость возводить здания и сооружения, человек эмпирическим путём пришёл к пониманию важности прямых углов. А как отмерить прямой угол, не имея геодезических приборов?
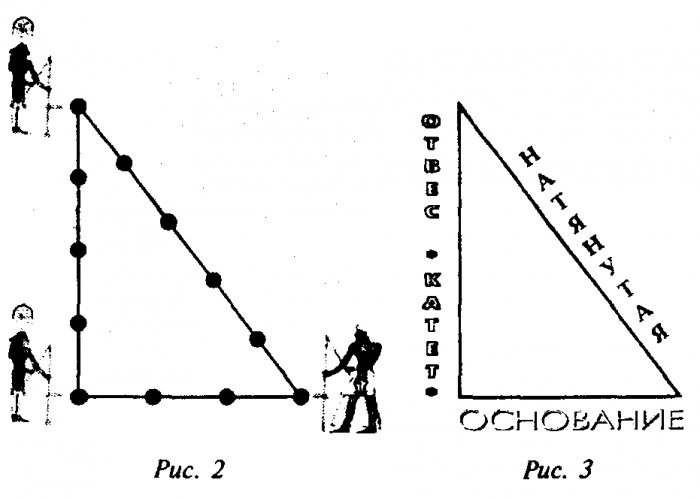
Оказывается, очень просто. Берём верёвку и делим её на 12 равных частей – например, при помощи складывания. Выбираем отрезок верёвки, равный 5, так, чтобы он находился межды двумя другими, равными 3 и 4. Выпрямляем его и фиксируем на ровном участке земли при помощи двух колышков. А затем натягиваем концы верёвки и сводим их в одну точку, чтобы получился треугольник. Прямоугольный, египетский.
«Делай, как делается». Знаменитая древнеегипетская пословица, дошедшая до наших дней. У нас её обычно понимают, как мудрое наблюдение: если так получается, значит, так правильно. Но при этом часто забывают культурно-исторический контекст Древнего Египта. Всеми работами руководили жрецы – члены замкнутой касты харнителей священного, древнего знания. Поэтому «делай, как делается» в древнеегипетском контексте наверняка значило «делай как говорят и не задавай лишних вопросов». То есть жрецы знали не только, «как» делать, чтобы «делалось», но и «почему», и это зание было скрыто от непосвящённых.
Мы тоже хотим знать, «почему». Нам недостаточно «как». Человеческий ум будоражат разнообразные загадки, и так, наверное, будет всегда. Египетский треугольник, хоть и известен с незапамятных времён – одна из таких загадок.
Начнём с того, что он красив. Его форма проста и гармонична, на него приятно смотреть. И с ним легко работать, используя самые простые инструменты – линейку и циркуль. Он, казалось бы, даже приглашает поработать с ним. Что ж, примем приглашение и посмотрим, что у нас получится.
Несколько простых построений, в числе которых – квадраты гипотенузы и катетов, а также симметричные отображения, сразу дают нам красивые, грмоничные фигуры. Здесь мы видим и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих (возрастающих) по размерам египетских треугольников в соответствии с правилом золотого сечения. Удивительное богатство гармоничных пропорций. И кажется, что ещё немного, и неразрешимая задача о квадратуре круга будет решена.
Впрочем, не станем уподобляться безумцам, которые изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Ограничимся констатацией бесконечных возможностей создания красоты и гармонии при помощи простой верёвки, разделённой на 12 равных частей. В том числе и картины в стиле арифмизма. Картины, которая, в соответствии с определением, изображает законченное арифметическое выражение: 9 + 16 = 25. Математический и геометрический смысл очевиден. Тайное значение – наверное, на то оно и тайное, чтобы таковым оставаться. А многозначительная и почти мистическая эстетика данных форм пусть радует глаз и будоражит воображение.
- Египетский треугольник, его свойства
- История египетского треугольника
- Египетский треугольник в строительстве
- Альтернативные способы построить прямой угол на 90 градусов
- Как получить египетский треугольник при помощи верёвки
- Как построить угол в 45, 30 и 60 градусов
- Итоги
- Египетский треугольник — загадка древности
- История открытия
- Применение
- Доказательство
- 📹 Видео
Видео:Египетский треугольникСкачать

Египетский треугольник, его свойства
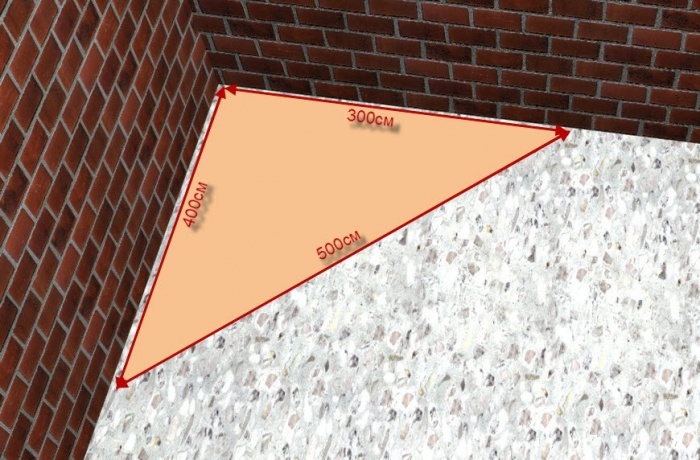
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
Видео:Пифагоровы тройки 1. Египетский треугольникСкачать

История египетского треугольника
Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.
Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.
Видео:Египетский треугольник. Пифагоровы тройки.Скачать

Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Видео:Теорема Пифагора для чайников)))Скачать

Итоги
Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Египетский треугольник — загадка древности
Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.
Видео:Найдите сторону треугольника на рисункеСкачать

История открытия
Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а
Видео:Египетский треугольник #огэ #математика #shortsСкачать

Применение
Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.
Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других – 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.
Видео:Египетский треугольникСкачать

Доказательство
При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.
📹 Видео
Что такое египетский треугольник?Скачать

Полуокружность в египетском треугольнике.Скачать
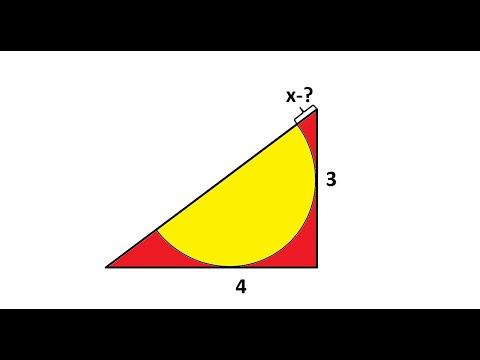
Найдите третью сторону треугольникаСкачать

Задача, которую исключили из экзамена в АмерикеСкачать

Решали пол-урока, а оказалось очень простоСкачать

8 класс, 16 урок, Теорема ПифагораСкачать

Египетский треугольникСкачать

Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Египетский треугольник, теорема ПифагораСкачать

Найдите стороны треугольникаСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать