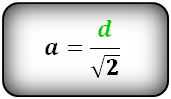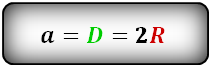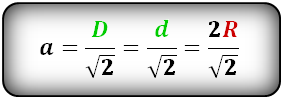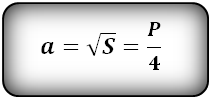1. Формула стороны квадрата через диагональ
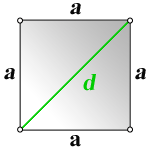
a — сторона квадрата
d — диагональ квадрата
Формула стороны квадрата, ( a ):
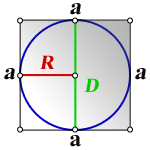
2. Формула стороны квадрата через радиус вписанной окружности
a — сторона квадрата
R — радиус вписанной окружности
D — диаметр вписанной окружности
Формула стороны квадрата, ( a ):
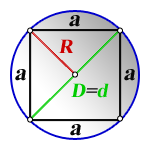
3. Формула стороны квадрата через радиус описанной окружности
a — сторона квадрата
R — радиус описанной окружности
D — диаметр описанной окружности
d — диагональ
Формула стороны квадрата, ( a ):
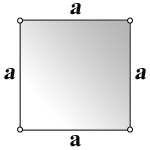
4. Формула стороны квадрата через площадь и периметр
a — сторона квадрата
S — площадь квадрата
P — периметр квадрата
Формула стороны квадрата, ( a ):
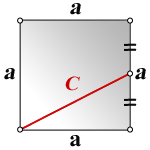
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a — сторона квадрата
C — линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, ( a ):
- Формулы квадрата
- Свойства квадрата
- Сторона квадрата
- Площадь квадрата
- Периметр квадрата
- Диагональ квадрата
- Вписанная окружность
- Описанная окружность
- Квадрат. Онлайн калькулятор
- Свойства квадрата
- Диагональ квадрата
- Окружность, вписанная в квадрат
- Формула вычисления радиуса вписанной окружности через сторону квадрата
- Формула вычисления сторон квадрата через радиус вписанной окружности
- Окружность, описанная около квадрата
- Формула радиуса окружности описанной вокруг квадрата
- Формула стороны квадрата через радиус описанной около квадрата окружности
- Периметр квадрата
- Признаки квадрата
- 📺 Видео
Видео:Как найти сторону квадрата в который вписаны 2 окружностиСкачать

Формулы квадрата
Для расчёта всех основных параметров квадрата воспользуйтесь калькулятором.
Свойства квадрата
- Длины сторон квадрата равны.
- Все углы квадрата прямые, равны 90°.
- Противолежащие стороны квадрата параллельны друг другу.
- Сумма всех углов квадрата равна 360°.
- Величина угла между диагональю и стороной равна 45°.
- Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
- Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
- Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
- Пересечение диагоналей является центром вписанной и описанной окружности.
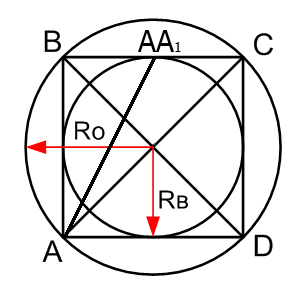
Сторона квадрата
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата | |
| RВ – радиус вписанной окружности | |
| RO – радиус описанной окружности | |
| AA1 — линия выходящая из угла на середину стороны квадрата |
Стороны квадрата через диагональ
Стороны квадрата через радиус вписанной окружности
Стороны квадрата через радиус описанной окружности
Стороны квадрата через площадь, S
Стороны квадрата через периметр, P
Стороны квадрата через линию выходящую из угла на середину стороны квадрата, AA1
Площадь квадрата
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата |
Площадь квадрата через сторону
Площадь квадрата через диагональ
Периметр квадрата
| Где: | AB – сторона квадрата |
$$ P = 4 * AB $$
Диагональ квадрата
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата | |
| S – площадь квадрата | |
| P – периметр квадрата |
Диагональ квадрата через сторону
Диагональ квадрата через площадь
Диагональ квадрата через периметр
Вписанная окружность
| Где: | AB – сторона квадрата |
Радиус вписанной окружности
Длина окружности, L
Площадь окружности, S
Описанная окружность
| Где: | AB – сторона квадрата |
| AC(BD) – диагональ квадрата |
Радиус описанной окружности через сторону
Радиус описанной окружности через диагональ
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
 |
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Видео:СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
      |
Видео:№450. Найдите сторону квадрата, если его площадь равна: а) 16 см2; б) 2,25 дм2; в) 12 м2.Скачать

Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
 . . | (1) |
Из равенства (1) найдем d:
 . . | (2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
 |
Ответ:
Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
 |
Видео:Как найти сторону квадрата через радиус?Скачать
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 | (3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
 |
Ответ:
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 | (4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
 |
Ответ:
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
 |
Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
 | (5) |
Из формулы (5) найдем R:
 |
 | (6) |
или, умножая числитель и знаменатель на 
 . . | (7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
 |
Ответ:
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 |
 . . | (8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
 |
Ответ:
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 | (9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
 |
Ответ:
Видео:16)Радиус окружности, описанной около квадрата, равен 8√2. Найдите длину стороны этого квадрата.Скачать
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
 |
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 | (10) |
Так как AD и BC перпендикулярны, то
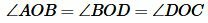 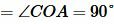 | (11) |
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 | (12) |
Эти реугольники также равнобедренные. Тогда
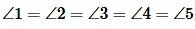 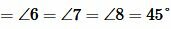 | (13) |
Из (13) следует, что
 | (14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
📺 Видео
Найти длину стороны квадрата, вписанного интересным способомСкачать

Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Как найти сторону квадрата по его периметруСкачать

Найти площадь квадрата описанного около окружности радиуса 19Скачать

Радиус описанной окружностиСкачать

2095 Найдите сторону квадрата вписанного в окружность радиуса 18 корней из 2Скачать

Радиус окружности рассчитываем через длину стороны квадратаСкачать
Геометрия. ОГЭ по математике. Задание 16Скачать