Как найти расстояние от центра окружности до прямой

Расстояние между двумя фигурами

Общее определение расстояния между двумя произвольными фигурами выходит за рамки школьной программы, и мы его не приводим. Ряд частных случаев, когда расстояние между двумя фигурами можно ввести на базе школьного материала, перечислен в следующей таблице.

Фигуры	Рисунок	Определение расстояния
Две точки		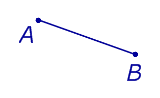Расстоянием между двумя точками называют длину отрезка AB.
Точка, лежащая на прямой		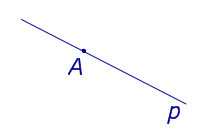Расстояние равно 0.
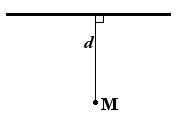
Точка, не лежащая на прямой		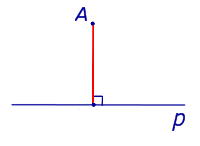Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.
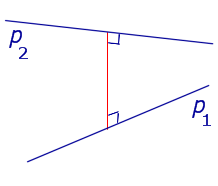
Две параллельные прямые		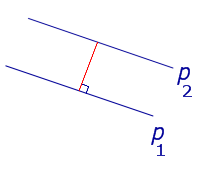Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.
Две пересекающиеся прямые		Расстояние равно 0.
Две скрещивающиеся прямые		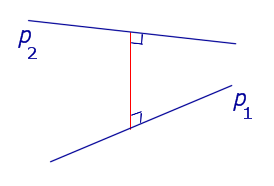Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.
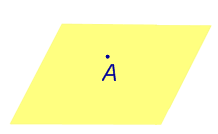
Точка, лежащая на плоскости		Расстояние равно 0.
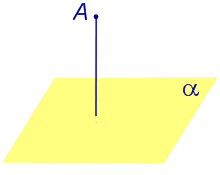
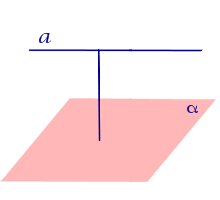
Точка, не лежащая на плоскости		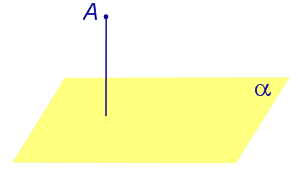Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.
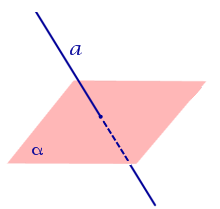
Прямая, пересекающая плоскость		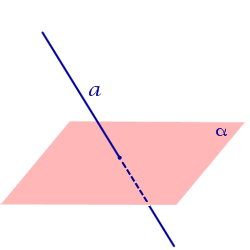Расстояние равно 0.
Прямая, лежащая на плоскости		Расстояние равно 0.
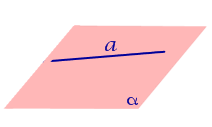
Прямая, параллельная плоскости		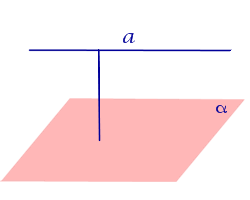Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.
Две пересекающиеся плоскости		Расстояние равно 0.
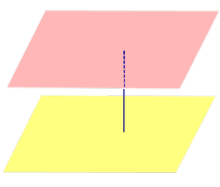
Две параллельные плоскости		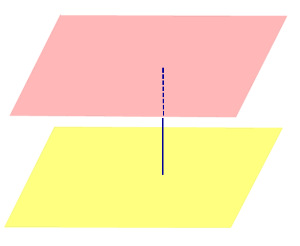Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).
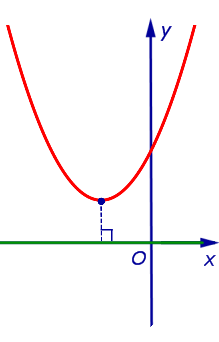
Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс		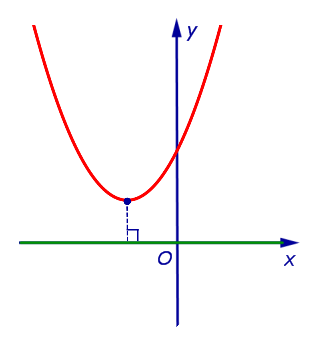Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс. Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.
Окружность и не пересекающая ее прямая		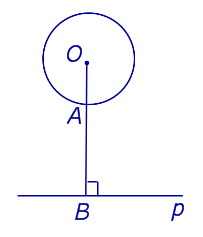Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности, а другой конец – на прямой. Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A, то расстояние от окружности до прямой равно длине отрезка AB.
Две непересекающиеся окружности, каждая из которых лежит вне другой		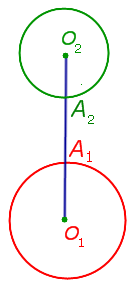Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности , а другой конец – на другой окружности. Если линия центров O1O2 пересекает окружность с центром O1 в точке A1, а окружность с центром O2 – в точке A2, то расстояние между окружностями будет равно длине отрезка A1A2.
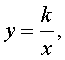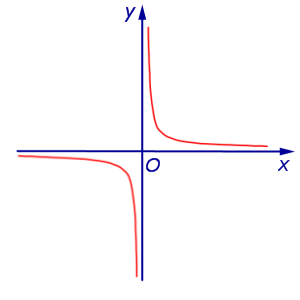Гипербола где k – любое, отличное от нуля, число, и ось абсцисс.		Расстояние между гиперболой и осью абсцисс считается равным 0, поскольку гипербола неограниченно приближается к оси абсцисс (длина отрезка, один из концов которого лежит на гиперболе, а другой конец – на оси абсцисс, может быть сколь угодно малой).

Две точки

Определение расстояния:
Расстоянием между двумя точками называют длину отрезка AB.

Точка, лежащая на прямой

Расстояние равно 0.

Точка, не лежащая на прямой

Определение расстояния:
Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.

Две параллельные прямые параллельные прямые

Определение расстояния:
Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.

Две пересекающиеся прямые пересекающиеся прямые

Расстояние равно 0.

Определение расстояния:
Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.

Точка, лежащая на плоскости

Расстояние равно 0.

Точка, не лежащая на плоскости

Определение расстояния:
Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.

Расстояние равно 0.

Расстояние равно 0.

Определение расстояния:
Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.

Две пересекающиеся плоскости

Расстояние равно 0.

Две параллельные плоскости

Определение расстояния:
Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).

Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс

Определение расстояния:
Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс.
Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.

Окружность и не пересекающая ее прямая

Определение расстояния:
Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности , а другой конец – на прямой.
Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A , то расстояние от окружности до прямой равно длине отрезка AB.

Две непересекающиеся окружности, каждая из которых лежит вне другой Две непересекающиеся окружности, каждая из которых лежит вне другой

Определение расстояния:
Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности, а другой конец – на другой окружности.
Если линия центров O₁O₂ пересекает окружность с центром O₁ в точке A₁, а окружность с центром O₂ – в точке A₂, то расстояние между окружностями будет равно длине отрезка A₁A₂.

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Расстояние от точки до прямой на плоскости.

Формула для вычисления расстояния от точки до прямой на плоскости

Если задано уравнение прямой A x + B y + C = 0, то расстояние от точки M(M _x , M _y ) до прямой можно найти, используя следующую формулу

d =	|A·M x + B·M y + C|
	√ A 2 + B 2

Примеры задач на вычисление расстояния от точки до прямой на плоскости

Решение. Подставим в формулу коэффициенты прямой и координаты точки

d =	|3·(-1) + 4·3 — 6|	=	|-3 + 12 — 6|	=	|3|	= 0.6
	√ 3 2 + 4 2		√ 9 + 16		5

Ответ: расстояние от точки до прямой равно 0.6.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Начертите какую-нибудь окружность и прямую, её не пересекающую. Найдите расстояние от центра окружности до прямой. Отметьте на окружности точку, ближайшую к данной прямой.

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,989
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Окружность

Вы будете перенаправлены на Автор24

Определение окружности

Окружность — геометрическая фигура, состоящая из всех точек, расположенных на равном расстоянии от заданной точки.

В рамках определения 1, заданная точка называется центром окружности.

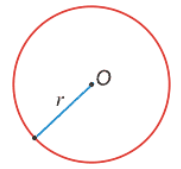
Отрезок, соединяющий центр окружности с любой ее точкой называется радиусом окружности $(r)$ (Рис. 1).

Рисунок 1. Окружность с центром в точке $O$ и радиусом $r$

Отрезок, соединяющий две любые точки окружности, называется хордой.

Хорда, проходящая через центр окружности, называется диаметром $(d)$.

Взаимное расположение прямой и окружности

Окружность имеет три возможных взаимных расположений относительно прямой:

Если расстояние от центра окружности до прямой меньше радиуса, то прямая имеет две точки пересечения с окружностью.

Если расстояние от центра окружности до прямой равно радиусу, то прямая имеет две точки пересечения с окружностью.

Если расстояние от центра окружности до прямой больше радиуса, то прямая имеет две точки пересечения с окружностью.

Уравнение окружности

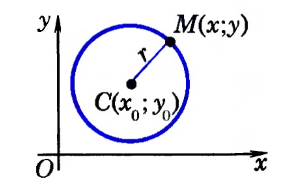
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).

Рисунок 2. Окружность в декартовой системе координат

Готовые работы на аналогичную тему

Расстояние от центра окружности до точки $M$ вычисляется следующим образом

Но, так как $M$ лежит на окружности, то по определению 3, получаем $CM=r$. Тогда получим следующее

Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.

В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид

Длина окружности

Выведем формулу длины окружности $C$ через её радиус. Для этого рассмотрим две окружности с длинами $C$ и $C’$ и радиусами $R$ и $R’$. Впишем в ним правильные $n-угольники$ с периметрами $P$ и $P’$ и длинами сторон $a$ и $a’$ соответственно. Как нам известно, сторона вписанного -угольника равна

Неограниченно увеличивая количество сторон правильных многоугольников $n$ получим, что

Получили, что отношение длины окружности к её диаметру постоянное число для любой окружности. Эту константу принято обозначать числом $pi approx 3,14$. Таким образом, получим

Формула (2) и есть формула для вычисления длины окружности.

Пример задачи на понятие окружность

Найти уравнение окружности с центром в точке $(1, 2)$. Проходящей через начало координат и найти длину данной окружности.

Решение.

Найдем сначала уравнение данной окружности. Для этого будем использовать формулу (1). Так как центр окружности лежит в точке $(1, 2)$, получим

Найдем радиус окружности как расстояние от точки $(1, 2)$ до точки $(0,0)$

Получаем, уравнение окружности имеет вид:

Найдем длину окружности по формуле (2). Получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2021

📽️ Видео