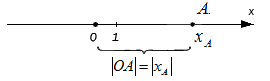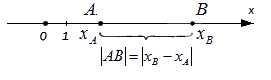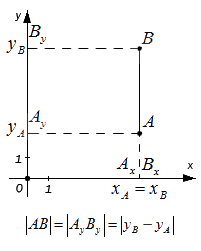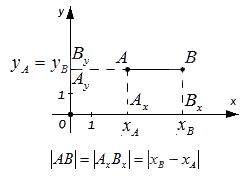В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Расстояние между точками на координатной прямой
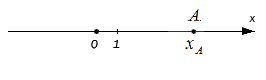
Исходные данные: координатная прямая O x и лежащая на ней произвольная точка А . Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число х A , оно же – координата точки А .
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О , необходимо будет отложить три единичных отрезка. Если точка А имеет координату — 4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние О А равно 3 ; во втором случае О А = 4 .
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О ) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4 111 .
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то O A = x A (число принимается за расстояние); если координата меньше нуля, то O A = — x A . В общем, эти утверждения справедливы для любого действительного числа x A .
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- x A , если x A > 0 ;
- — x A , если x A 0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B , лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты x A и x B : A B = x B — x A .
Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Расстояние между точками на плоскости
Исходные данные: точки A и B , лежащие на плоскости в прямоугольной системе координат O x y с заданными координатами: A ( x A , y A ) и B ( x B , y B ) .
Проведем через точки А и B перпендикуляры к осям координат O x и O y и получим в результате точки проекции: A x , A y , B x , B y . Исходя из расположения точек А и B далее возможны следующие варианты:
— если точки А и В совпадают, то расстояние между ними равно нулю;
— если точки А и В лежат на прямой, перпендикулярной оси O x (оси абсцисс), то точки и совпадают, а | А В | = | А y B y | . Поскольку, расстояние между точками равно модулю разности их координат, то A y B y = y B — y A , а, следовательно A B = A y B y = y B — y A .
— если точки A и B лежат на прямой, перпендикулярной оси O y (оси ординат) – по аналогии с предыдущим пунктом: A B = A x B x = x B — x A
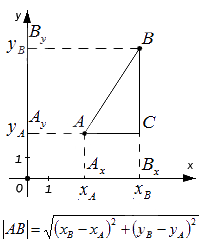
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
Мы видим, что треугольник А В С является прямоугольным по построению. При этом A C = A x B x и B C = A y B y . Используя теорему Пифагора, составим равенство: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 , а затем преобразуем его: A B = A x B x 2 + A y B y 2 = x B — x A 2 + y B — y A 2 = ( x B — x A ) 2 + ( y B — y A ) 2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
A B = ( x B — x A ) 2 + ( y B — y A ) 2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: A B = ( x B — x A ) 2 + ( y B — y A ) 2 = 0 2 + 0 2 = 0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
A B = ( x B — x A ) 2 + ( y B — y A ) 2 = 0 2 + ( y B — y A ) 2 = y B — y A
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
A B = ( x B — x A ) 2 + ( y B — y A ) 2 = ( x B — x A ) 2 + 0 2 = x B — x A
Видео:Как искать точки на тригонометрической окружности.Скачать

Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат O x y z с лежащими на ней произвольными точками с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить расстояние между этими точками.
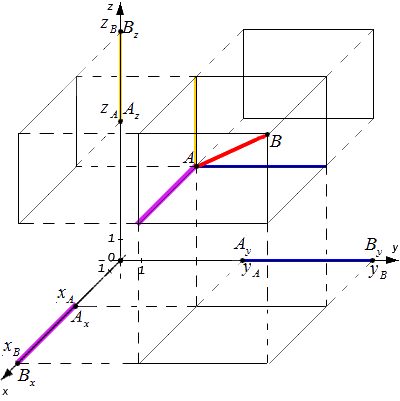
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: A x , A y , A z , B x , B y , B z
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: A x B x , A y B y и A z B z
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
A x B x = x B — x A , A y B y = y B — y A , A z B z = z B — z A
A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B — x A 2 + y B — y A 2 + z B — z A 2 = = ( x B — x A ) 2 + ( y B — y A ) 2 + z B — z A 2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
A B = x B — x A 2 + y B — y A 2 + ( z B — z A ) 2
Полученная формула действительна также для случаев, когда:
— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A ( 1 — 2 ) и B ( 11 + 2 ) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B .
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 — 2 = 2 — 1
- Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 — ( 1 — 2 ) = 10 + 2 2
Ответ: O A = 2 — 1 , A B = 10 + 2 2
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A ( 1 , — 1 ) и B ( λ + 1 , 3 ) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние А В будет равно 5 .
Решение
Чтобы найти расстояние между точками A и B , необходимо использовать формулу A B = ( x B — x A ) 2 + y B — y A 2
Подставив реальные значения координат, получим: A B = ( λ + 1 — 1 ) 2 + ( 3 — ( — 1 ) ) 2 = λ 2 + 16
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Ответ: А В = 5 , если λ = ± 3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат O x y z и лежащие в нем точки A ( 1 , 2 , 3 ) и B — 7 , — 2 , 4 .
Решение
Для решения задачи используем формулу A B = x B — x A 2 + y B — y A 2 + ( z B — z A ) 2
Подставив реальные значения, получим: A B = ( — 7 — 1 ) 2 + ( — 2 — 2 ) 2 + ( 4 — 3 ) 2 = 81 = 9
Видео:Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Видео:Расстояние от точки до плоскости / Вывод формулыСкачать

Наименьшее расстояние между точкой и окружностью
Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.
Примеры:
Подход :
который равен (др)
d = √ ((x2-x1) ^ 2 — (y2-y1) ^ 2)

Ниже приведена реализация вышеуказанного подхода:
// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include
using namespace std;
// Функция для поиска кратчайшего расстояния
void dist( double x1, double y1, double x2, double y2, double r)
cout «The shortest distance «
«between a point and a circle is «
sqrt (( pow ((x2 — x1), 2))
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
System.out.println( «The shortest distance «
+ «between a point and a circle is «
+ (Math.sqrt((Math.pow((x2 — x1), 2 ))
+ (Math.pow((y2 — y1), 2 )))
public static void main(String[] args)
double x1 = 4 , y1 = 6 ,
x2 = 35 , y2 = 42 , r = 5 ;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг
# Функция поиска кратчайшего расстояния
def dist(x1, y1, x2, y2, r):
print ( «The shortest distance between a point and a circle is «
,((((x2 — x1) * * 2 ) + ((y2 — y1) * * 2 )) * * ( 1 / 2 )) — r);
dist(x1, y1, x2, y2, r);
# Этот код предоставлен 29AjayKumar
// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
Console.WriteLine( «The shortest distance «
+ «between a point and a circle is «
+ (Math.Sqrt((Math.Pow((x2 — x1), 2))
+ (Math.Pow((y2 — y1), 2)))
public static void Main(String[] args)
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
function dist( $x1 , $y1 , $x2 , $y2 , $r )
echo «The shortest distance between a point and a circle is «
💡 Видео
Расстояние. Математика. 6 классСкачать

10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Расстояние от точки до прямойСкачать

✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Урок 10. Расстояние от точки до плоскости. Компенсация расстояний. Стереометрия с нуля.Скачать

Определение расстояния от точки до плоскости треугольникаНатуральная величина расстоянияСкачать
Топография. Как измерить расстояние от одной точки до другой на карте. КПЗ.Скачать

#30. Как найти расстояние от точки до плоскости?Скачать

Определить расстояние от точки С до прямой АВ. Метод прямоугольного треугольника.Скачать

Расстояние от точки до различных поверхностейСкачать

расстояние от точки до плоскостиСкачать