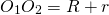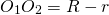Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Расстояние между центрами пересекающихся окружностей
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Геометрия. 9 класс
- НАШИ ПАРТНЁРЫ
- Взаимное расположение окружностей
- Расстояние между центрами двух пересекающихся окружностей, если даны радиусы и общая длина хорды
- 🎦 Видео
Видео:Сможешь найти расстояние между центрами пересекающихся окружностей?Скачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутреннее касание двух окружностей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружности пересекаются в двух точках | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешнее касание двух окружностей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Каждая из окружностей лежит вне другой | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Формула | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Общая хорда двух пересекающихся окружностей |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям | |||||||||
| Внутренняя касательная к двум окружностям | |||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Расстояние между центрами. Окружность. Математика 10-11 классы.Скачать  Расстояние между центрами пересекающихся окружностейВидео:Геометрия Общая хорда двух пересекающихся окружностей видна из их центров под углами 90 и 60. НайтиСкачать  Две окружности на плоскости. | |||||||||
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать
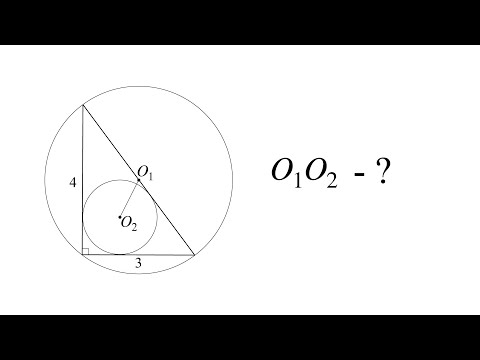
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | ||||||||||||||
| Внутренняя касательная к двум окружностям | ||||||||||||||
| Внутреннее касание двух окружностей | ||||||||||||||
| Окружности пересекаются в двух точках | ||||||||||||||
| Внешнее касание двух окружностей | ||||||||||||||
| Каждая из окружностей лежит вне другой | ||||||||||||||
| Фигура | Рисунок | Формула |
| Внешняя касательная к двум окружностям |  |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Как найти расстояние между центрами | Олимпиадная математикаСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Задание 24 Две пересекающиеся окружностиСкачать 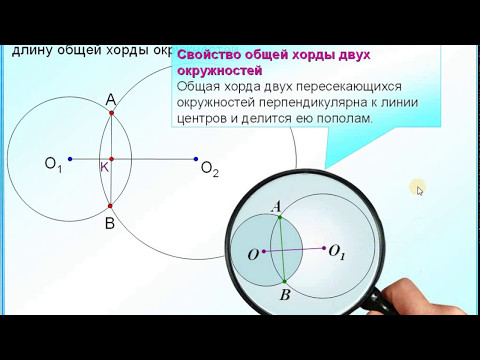 Геометрия. 9 классДве окружности могут пересекаться, не пересекаться либо касаться друг друга. Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов: Кольцом называют фигуру, заключенную между концентрическими окружностями. Видео:Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать  НАШИ ПАРТНЁРЫ © Государственная образовательная платформа «Российская электронная школа» Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать  Взаимное расположение окружностейВыясним, каким может быть взаимное расположение двух окружностей. Две окружности могут пересекаться, не пересекаться либо касаться друг друга. I. Пересекающиеся окружности имеют две общие точки. Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов: II. Не пересекающиеся окружности не имеет общих точек. Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:
III. Касающиеся окружности имеют одну общую точку — точку касания. При внешнем касании расстояние между центрами окружностей равно сумме их радиусов: При внутреннем касании расстояние между центрами равно разности радиусов: Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0. Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать  Расстояние между центрами двух пересекающихся окружностей, если даны радиусы и общая длина хордыДаны два круга с заданными радиусами, которые пересекаются и имеют общий аккорд. Длина общего аккорда дается. Задача состоит в том, чтобы найти расстояние между центрами двух окружностей. Примеры: Подход :
Ниже приведена реализация вышеуказанного подхода: // C ++ программа для поиска 🎦 ВидеоМ1152. Расстояние между центрами вписанной и описанной окружностейСкачать 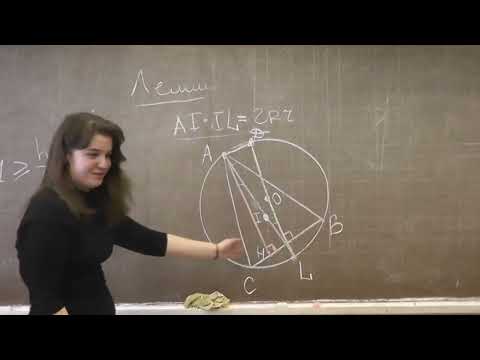 ✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать  Математика Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояние между ихСкачать  Алгоритмы. Пересечение окружностейСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  9 класс, 8 урок, Взаимное расположение двух окружностейСкачать  1 2 4 сопряжение окружностейСкачать  Быстро и легко определяем центр любой окружностиСкачать  |



































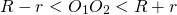


 Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:
Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов: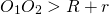 R + r]» title=»Rendered by QuickLaTeX.com»/>
R + r]» title=»Rendered by QuickLaTeX.com»/>