 Числовая ось |
| Прямоугольная декартова система координат на плоскости |
| Формула для расстояния между двумя точками координатной плоскости |
| Уравнение окружности на координатной плоскости |
- Числовая ось
- Прямоугольная декартова система координат на плоскости
- Формула для расстояния между двумя точками координатной плоскости
- Уравнение окружности на координатной плоскости
- Как найти расстояние между центрами окружностей
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Ответ
- Проверено экспертом
- Найти расстояние между центрами окружностей по координатам
- Как найти расстояние между центрами окружностей
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Ответ
- Проверено экспертом
- Декартовы координаты точек плоскости. Уравнение окружности
- Числовая ось
- Прямоугольная декартова система координат на плоскости
- Формула для расстояния между двумя точками координатной плоскости
- Уравнение окружности на координатной плоскости
- Пересечение двух окружностей
- Точки пересечения двух окружностей
- Первая окружность
- Вторая окружность
- Пересечение окружностей
Видео:Расстояние между центрами. Окружность. Математика 10-11 классы.Скачать
Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Видео:Как найти расстояние между центрами | Олимпиадная математикаСкачать
Прямоугольная декартова система координат на плоскости
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Видео:Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать
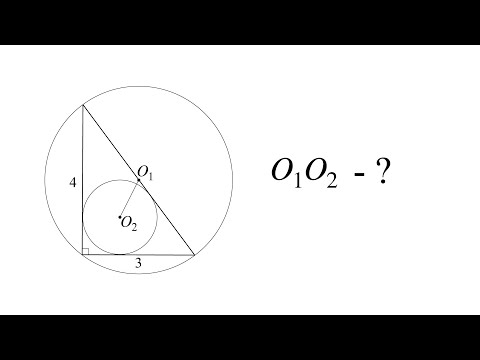
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . | (1) |
что и требовалось доказать.
Видео:Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать
Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать
Как найти расстояние между центрами окружностей
У Вас недостаточно прав для добавления комментариев.
Вам необходимо зарегистрироваться на сайте
Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!
| Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям | |
 | |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
| Фигура | Рисунок | Формула | ||
| Внешняя касательная к двум окружностям |  | |||
| Внутренняя касательная к двум окружностям |  | |||
| Общая хорда двух пересекающихся окружностей |  | |||
| Внешняя касательная к двум окружностям | |
| |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям | |||||||||
| Внутренняя касательная к двум окружностям | |||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Длина отрезкаСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Уравнение окружности (1)Скачать  ОтветПроверено экспертомУравнение окружности с центром (a;b) и радиусом R центр окружности (-2;6) радиус 6 центр окружности (4;-5)радиус 5 по формуле расстояние между двумя точками : находим расстояние между центрами заданных окружностей Видео:✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать  Найти расстояние между центрами окружностей по координатамВидео:Как найти координаты точек на тригонометрической окружностиСкачать  Как найти расстояние между центрами окружностейУ Вас недостаточно прав для добавления комментариев. Все права защищены 2019
Видео:Расстояние от точки до прямой (метод координат)Скачать  Взаимное расположение двух окружностей
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей | |||||||||
| Каждая из окружностей лежит вне другой | | ||||||||
| Внешнее касание двух окружностей | | ||||||||
| Внутреннее касание двух окружностей | | ||||||||
| Окружности пересекаются в двух точках | | | |||||||
| Каждая из окружностей лежит вне другой | |||||||||
| |||||||||
| Внешнее касание двух окружностей | |||||||||
| |||||||||
| Внутреннее касание двух окружностей | |||||||||
| |||||||||
| Окружности пересекаются в двух точках | |||||||||
| |||||||||
| |||||||||
| Каждая из окружностей лежит вне другой | |||||||||
Расстояние между центрами окружностей больше суммы их радиусов | |||||||||
| Внешнее касание двух окружностей | |||||||||
Расстояние между центрами окружностей равно сумме их радиусов | |||||||||
| Внутреннее касание двух окружностей | |||||||||
| Окружности пересекаются в двух точках | |||||||||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. | |||||||||
| Внутренняя касательная к двум окружностям | | ||||||||
| Внутреннее касание двух окружностей | | ||||||||
| Окружности пересекаются в двух точках | | ||||||||
| Внешнее касание двух окружностей | | ||||||||
| |||||||||
| |||||||||
| Внешняя касательная к двум окружностям | |
| |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
| Фигура | Рисунок | Формула | ||
| Внешняя касательная к двум окружностям | | |||
| Внутренняя касательная к двум окружностям | | |||
| Общая хорда двух пересекающихся окружностей | | |||
| Внешняя касательная к двум окружностям | |
| |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям | |||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||||||||||
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Найти центр и радиус окружностиСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Расстояние от точки до плоскости / Вывод формулыСкачать  ОтветПроверено экспертомУравнение окружности с центром (a;b) и радиусом R центр окружности (-2;6) радиус 6 центр окружности (4;-5)радиус 5 по формуле расстояние между двумя точками : находим расстояние между центрами заданных окружностей Видео:расстояние между центрамиСкачать  Декартовы координаты точек плоскости. Уравнение окружности
Видео:8 класс. Координаты середины отрезка. Расстояние между точками. Уравнение окружности. КонтрольнаяСкачать  Числовая осьОпределение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом . Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA . Видео:9 класс, 6 урок, Уравнение окружностиСкачать  Прямоугольная декартова система координат на плоскостиОпределение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо. Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy . Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) . Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5). Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью . Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0. Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать  Формула для расстояния между двумя точками координатной плоскостиУтверждение 1 . Расстояние между двумя точками координатной плоскости вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
что и требовалось доказать. Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем: Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) . Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид Пересечение двух окружностейЭтот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности. Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностейПервая окружностьВторая окружностьПересечение окружностейСама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2. При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже: Сначала калькулятор находит отрезок a Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде): И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения: Обратите внимание на разные знаки перед вторым слагаемым По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres |
