Определение треугольника по погорелова

Вопрос 1. Дайте определение косинуса острого угла прямоугольного треугольника.
Ответ. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
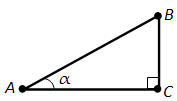
Косинус угла (alpha) обозначается так: (cos alpha). На рисунке 147 показан прямоугольный треугольник ABC с углом A, равным (alpha). Косинус угла (alpha) равен отношению катета AC, прилежащего к этому углу, к гипотенузе AB, т.е.

Вопрос 2. Докажите, что косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.
Ответ. Теорема 7.1. Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.
Это означает, что у двух прямоугольных треугольников с одним и тем же острым углом косинусы этого угла равны.
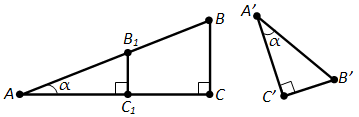
Доказательство. Пусть ABC и A’B’C’ — два прямоугольных треугольника с одним и тем же углом при вершинах A и A’, равным (alpha) (рис. 148). Требуется доказать, что

Построим треугольник AB₁C₁, равный треугольнику A’B’C’, как показано на рисунке 148. Так прямые BC и B₁C₁ перпендикулярны прямой AC, то они параллельны. По теореме о пропорциональных отрезках

А так как по построению AC₁ = A’C’, AB₁ = A’B’, то

Вопрос 3. Докажите теорему Пифагора.
Ответ. Теорема 7.2 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
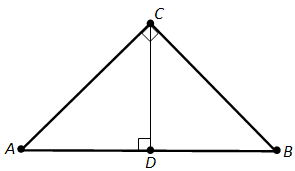
Доказательство.Пусть ABC – данный прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла C (рис. 149).

По определению косинуса угла (cos A = frac = frac). Отсюда (AB cdot AD = AC^2). Аналогично (cos B = frac = frac). Отсюда (AB cdot BD = BC^2). Складывая полученные равенства почленно и замечая, что (AD + DB = AB), получим:

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Определение треугольника по погорелова

Четырёхугольником называется фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырёхугольника, а соединяющие их отрезки — сторонами четырёхугольника.

Четырёхугольник называется вписанным, если все его вершины лежат на некоторой окружности, и описанным, если все его стороны касаются некоторой окружности.

Вершины четырёхугольника называются соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырёхугольника, называются диагоналями.

Стороны четырёхугольника, исходящие из одной вершины, называются соседними сторонами. Стороны, не имеющие общего конца, называются противолежащими сторонами.

Четырёхугольник обозначается указанием его вершин. Например, ABCD. В обозначении четырёхугольника рядом стоящие вершины должны быть соседними. Четырёхугольник ABCD можно также обозначить BCDA или DCBA. Но нельзя обозначить ABDC (В и D — не соседние вершины).

Сумма длин всех сторон четырёхугольника называется периметром.

Параллелограмм

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны, т. е. лежат на параллельных прямых.

Теорема 6.1. Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.

Свойство диагоналей параллелограмма

Теорема 6.2 . (обратная теореме 6.1) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Свойство противолежащих сторон и углов параллелограмма

Теорема 6.3 . У параллелограмма противолежащие стороны равны, противолежащие углы равны.

Прямоугольник

Прямоугольник — это параллелограмм, у которого все углы прямые.

Теорема 6.4 . Диагонали прямоугольника равны.

Ромб — это параллелограмм, у которого все стороны равны.

Теорема 6.5. Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов.

Квадрат

Квадрат — это прямоугольник, у которого все стороны равны. Так как стороны квадрата равны, то он является также ромбом. Поэтому квадрат обладает свойствами прямоугольника и ромба.

1. У квадрата все углы прямые.
2. Диагонали квадрата равны.
3. Диагонали квадрата пересекаются под прямым углом и являются биссектрисами его углов.

Теорема Фалеса

Теорема 6.6 . Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Замечание. В условии теоремы Фалеса вместо сторон угла можно взять любые две прямые, при этом заключение теоремы будет то же: параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекают равные отрезки и на другой прямой.

Средняя линия треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Теорема 6.7 . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

Трапеция

Трапецией называется четырёхугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.

Теорема 6.8. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Пропорциональные отрезки

Теорема 6.9 . Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Замечательные точки в треугольнике

Все три биссектрисы треугольника пересекаются в одной точке. Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке. Все три прямые, содержащие высоты к сторонам треугольника, тоже пересекаются в одной точке (ортоцентр треугольника). Все три медианы треугольника пересекаются в одной точке.

Окружность, описанную около треугольника, вершинами которого являются середины сторон данного треугольника, называют окружностью Эйлера (окружность девяти точек). Середины сторон треугольника и середины отрезков, соединяющих его ортоцентр с вершинами, лежат на одной окружности с центром О, являющейся по определению окружностью Эйлера.

Видео:6.4 - Геометрия 7-9 класс ПогореловСкачать

Раздел 2. Теорема Пифагора

Косинус угла

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинус угла а обозначается так: cos а и равен отношению катета АС, прилежащего к этому углу, к гипотенузе АВ, т. е. cos a = АС/АВ.

Теорема 7.1. Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.

Это означает, что у двух прямоугольных треугольников с одним и тем же острым углом косинусы этого угла равны.

Теорема Пифагора

Теорема 7.2. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Из теоремы Пифагора следует, что в прямоугольном треугольнике любой из катетов меньше гипотенузы. Отсюда, в свою очередь, следует, что cos а 2 + 4 2 = 5 2 ).

В связи с указанным способом построения прямого угла треугольник со сторонами 3, 4 и 5 единиц иногда называют египетским.

Перпендикуляр и наклонная

Пусть ВА — перпендикуляр, опущенный из точки В на прямую а, и С — любая точка прямой а, отличная от А. Отрезок ВС называется наклонной, проведённой из точки В к прямой а (рис. 153). Точка С называется основанием наклонной. Отрезок АС называется проекцией наклонной.

Из теоремы Пифагора следует, что если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше.

Неравенство треугольника

Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и В совпадают, то расстояние между ними принимается равным нулю.

Теорема 7.3. Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.

Это значит, что каждое из этих расстояний меньше суммы или равно сумме двух других. Заметим, что в случае, когда точки не лежат на одной прямой, в неравенстве треугольника строгое неравенство. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон.

Соотношения между сторонами и углами в прямоугольном треугольнике

Пусть АВС — прямоугольный треугольник с прямым углом С и острым углом при вершине А, равным а.

• Согласно определению cos а равен отношению катета, прилежащего к углу а, к гипотенузе.
• Синусом угла а (обозначается sin а) называется отношение противолежащего катета ВС к гипотенузе АВ: sin а = ВС/АВ.
• Тангенсом угла а (обозначается tg a) называется отношение противолежащего катета ВС к прилежащему катету АС: tg a = ВС/АС.
• Котангенсом угла а (обозначается ctg a) называется отношение прилежащего катета АС к противолежащему катету ВС: ctga = АС/ВС.

Синус, тангенс и котангенс утла, так же как и косинус, зависят только от величины угла. Из определения sin a, cos a, tg a и ctg a получаем следующие правила:

1. Катет, противолежащий углу а, равен произведению гипотенузы на sin a.
2. Катет, прилежащий к углу а, равен произведению гипотенузы на cos a.
3. Катет, противолежащий углу а, равен произведению второго катета на tg a.
4. Катет, прилежащий к углу а, равен произведению второго катета на ctg a.

Эти правила позволяют, зная одну из сторон прямоугольного треугольника и острый угол, находить две другие стороны; зная две стороны, находить острые углы.

Для sin a, cos a, tg a и ctg a составлены специальные таблицы . Эти таблицы позволяют по данному углу а найти sin a, cos a, tg a и ctg a или по значениям sin a, cos a, tg a и ctg a найти соответствующий угол. В настоящее время для этой цели обычно применяют микрокалькуляторы.

Основные тригонометрические тождества

Эти тождества позволяют, зная одну из величин sin a, cos a, tg a или ctg a, найти три другие.

1. tg a = sin a / cos a.
2. сtg a = cos a / sin a.
3. sin 2 a + cos 2 a = 1.
4. 1 + tg 2 a = 1 / cos 2 a
5. 1 + ctg 2 a = 1 / sin 2 a

Значения синуса, косинуса, тангенса и котангенса некоторых углов

Теорема 7.4. Для любого острого угла a: sin (90° — a) = cos a, cos (90° — a) = sin a.

Изменение синуса, косинуса, тангенса и котангенса при возрастании угла

Теорема 7.5 . При возрастании острого угла sin a и tg a возрастают, а cos a и ctg a убывают.

Видео:Неравенства треугольника. 7 класс.Скачать

Раздел 3. Декартовы координаты на плоскости

Определение декартовых координат

Проведём на плоскости через точку О две взаимно перпендикулярные прямые х и у — оси координат. Ось х (она обычно горизонтальная) называется осью абсцисс, а ось у — осью ординат. Точкой пересечения О — началом координат — каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая её стрелкой, а другую — отрицательной.

Каждой точке А плоскости мы сопоставим пару чисел — координаты точки — абсциссу (х) и ординату (у) по такому правилу.

Через точку А проведём прямую, параллельную оси ординат. Она пересечёт ось абсцисс х в некоторой точке Ах. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Ах. Это число будет положительным, если Ах принадлежит положительной полуоси, и отрицательным, если Ах принадлежит отрицательной полуоси. Если точка А лежит на оси у, то полагаем х равным нулю.

Ордината (у) точки А определяется аналогично. Через точку А проведём прямую, параллельную оси абсцисс х. Она пересечёт ось ординат у в некоторой точке Ау. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки Ау. Это число будет положительным, если Ау принадлежит положительной полуоси, и отрицательным, если Ау принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс х, то полагаем у равным нулю. Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: А (х; у) (на первом месте абсцисса, на втором — ордината).

Оси координат разбивают плоскость на четыре части — четверти: I, И, III, IV.

Точки оси х (оси абсцисс) имеют равные нулю ординаты (у = 0), а точки оси у (оси ординат) имеют равные нулю абсциссы (х = 0). У начала координат абсцисса и ордината равны нулю.

Плоскость, на которой введены описанным выше способом координаты х и у, будем называть плоскостью ху. Произвольную точку на этой плоскости с координатами х и у будем иногда обозначать просто (х; у). Введённые на плоскости координаты х и у называются декартовыми по имени Р. Декарта, который впервые применил их в своих исследованиях.

Координаты середины отрезка

Пусть А (х1; у1) и В (х2; у2) — две произвольные точки и С (х; у) — середина отрезка АВ. Найдём координаты х, у точки С.
х = (х1 + х2)/2; у = (у1 = у2)/2

Расстояние между точками

Пусть на плоскости ху даны две точки: А1 с координатами х1, у1 и А2 с координатами х2, у2. Выразим расстояние между точками А1 и А2 через координаты этих точек.
d 2 = (х₁ — х₂) 2 + (у₁ — у₂) 2
где d — расстояние между точками А1 и А2.

Уравнение окружности

Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры.

Составим уравнение окружности с центром в точке А0 (а; b) и радиусом R
(х — а) 2 + (у — b) 2 = R 2 .
Если центром окружности является начало координат, то уравнение окружности имеет вид: х 2 + у 2 = R 2 .

Уравнение прямой

Любая прямая в декартовых координатах х, у имеет уравнение вида ах + by + с = 0, где а, b, с — некоторые числа, причём хотя бы одно из чисел а, b не равно нулю.

Координаты точки пересечения прямых

Координаты точки пересечения являются решением системы уравнений, задающих прямые.

Расположение прямой относительно системы координат

Выясним, как расположена прямая относительно осей координат, если её уравнение ах + by + с = 0 имеет тот или иной частный вид.

1. а = 0, b ≠ 0. В этом случае уравнение прямой можно переписать так: у = -c/b. Таким образом, все точки прямой имеют одну и ту же ординату (-c/b); следовательно, прямая параллельна оси х. В частности, если с = 0, то прямая совпадает с осью х.
2. b = 0, а ≠ 0. Этот случай рассматривается аналогично. Прямая параллельна оси у и совпадает с ней, если и с = 0.
3. с = 0. Прямая проходит через начало координат, так как координаты (0; 0) удовлетворяют уравнению прямой.

Угловой коэффициент в уравнении прямой

Если в общем уравнении прямой ах + by + с = 0 коэффициент при у не равен нулю, то это уравнение можно разрешить относительно у. Получим y = -a/b, x = -c/b. Или, обозначая -a/b = k, -c/b = l, получим у = kx + l.

Коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью х. Коэффициент k в уравнении прямой называется угловым коэффициентом прямой.

График линейной функции

Графиком линейной функции является прямая.

Пересечение прямой с окружностью

Пусть R — радиус окружности и d — расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной,— за ось х (рис. 180). Тогда уравнением окружности будет х 2 + у 2 = R 2 , а уравнением прямой х = d.

Для того чтобы прямая и окружность пересекались, надо, чтобы система двух уравнений х2 + у2 = R2, х = d имела решение. И обратно: всякое решение этой системы даёт координаты х, у точки пересечения прямой с окружностью.

1. Окружность и прямая имеют две точки пересечения, если R > d.
2. Система имеет одно решение, т. е. прямая и окружность касаются, если R = d
3. Система не имеет решения, т. е. прямая и окружность не пересекаются, если R Раздел 4. Движение

Преобразование фигур

Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.

Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками, т. е. переводит любые две точки X и У одной фигуры в точки X’ и Y’ другой фигуры так, что ХУ = Х’У’.

Замечание. Понятие движения в геометрии связано с обычным представлением о перемещении. Но если мы представляем себе непрерывный процесс, то в геометрии для нас будут иметь значение только начальное и конечное положения фигуры. Два движения, выполненные последовательно, дают снова движение. Преобразование, обратное движению, также является движением.

Свойства движения

Теорема 9.1. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.

Это значит, что если точки А, В, С, лежащие на прямой, переходят в точки А1, В1, С1, то эти точки также лежат на прямой; если точка В лежит между точками А и С, то точка В1 лежит между точками А1 и С1.

Из теоремы 9.1 следует, что при движении прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки. При движении сохраняются углы между полупрямыми.

Симметрия относительно точки

Пусть О — фиксированная точка и X — произвольная точка плоскости. Отложим на продолжении отрезка ОХ за точку О отрезок ОХ’, равный ОХ. Точка X’ называется симметричной точке X относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке X’, есть точка X.

Преобразование фигуры F в фигуру F’, при котором каждая её точка X переходит в точку X’, симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом фигуры F и F’ называются симметричными относительно точки О (рис. 189).

Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется центрально-симметричной, а точка О называется центром симметрии.

Например, параллелограмм является центрально-симметричной фигурой. Его центр симметрии — точка пересечения диагоналей.

Теорема 9.2. Преобразование симметрии относительно точки является движением.

Симметрия относительно прямой

Пусть g — фиксированная прямая. Возьмём произвольную точку X и опустим перпендикуляр АХ на прямую g. На продолжении перпендикуляра за точку А отложим отрезок АХ’, равный отрезку АХ. Точка X’ называется симметричной точке относительно прямой g. Если точка X лежит на прямой g, то симметричная ей точка есть сама точка X. Очевидно, что точка, симметричная точке X’, есть точка X.

Преобразование фигуры F в фигуру F’, при котором каждая её точка X переходит в точку X’, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F’ называются симметричными относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.

Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно его сторонам, являются осями симметрии прямоугольника. Прямые, на которых лежат диагонали ромба, являются его осями симметрии.

Теорема 9.3. Преобразование симметрии относительно прямой является движением.

Поворот

Поворотом плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении.

Это значит, что если при повороте около точки О точка X переходит в точку X’, то лучи ОХ и ОХ’ образуют один и тот же угол, какова бы ни была точка X. Этот угол называется углом поворота. Преобразование фигур при повороте плоскости также называется поворотом.

Параллельный перенос и его свойства

Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (данное определение не является математически строгим).

Параллельный перенос задаётся формулами х = х + а, у’ = у + b. Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.

Параллельный перенос есть движение. Параллельный перенос сохраняет расстояния, а значит, является движением. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. При параллельном переносе прямая переходит в параллельную прямую (или в себя).

Существование и единственность параллельного переноса. Сонаправленность полупрямых

Теорема 9.4. Каковы бы ни были две точки А и А’, существует один и только один параллельный перенос, при котором точка А переходит в точку А’.

Две полупрямые называются одинаково направленными или сонаправленными, если они совмещаются параллельным переносом, т. е. существует параллельный перенос, который переводит одну полупрямую в другую.

Если полупрямые а и b одинаково направлены и полупрямые b и с одинаково направлены, то полупрямые а и с тоже одинаково направлены.

Две полупрямые называются противоположно направленными, если каждая из них одинаково направлена с полупрямой, дополнительной к другой.

Геометрические преобразования на практике

Известно, что геометрия как наука выросла из практического землемерия. А теперь сама она имеет большое прикладное значение. В частности, на практике широко используются геометрические преобразования

Равенство фигур

Две фигуры называются равными, если они движением переводятся одна в другую. Для обозначения равенства фигур используется обычный знак равенства. Запись F = F’ означает, что фигура F равна фигуре F’. В записи равенства треугольников: DАВС = DA1B1C1 — предполагается, что совмещаемые при движении вершины стоят на соответствующих местах. При таком условии равенство треугольников, определяемое через их совмещение движением, и равенство, как мы его понимали до сих пор, выражают одно и то же.

Это значит, что если у двух треугольников соответствующие стороны равны и соответствующие углы равны, то эти треугольники совмещаются движением. И обратно: если два треугольника совмещаются движением, то у них соответствующие стороны равны и соответствующие углы равны.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Раздел 5. Векторы

Абсолютная величина и направление вектора

Вектор — это направленный отрезок. Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами а, b, с, … . Можно также обозначать вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова «вектор» над буквенным обозначением вектора иногда ставится стрелка или черта.

Векторы АВ и CD называются одинаково направленными, если полупрямые АВ и CD одинаково направлены. Векторы АВ и CD называются противоположно направленными, если полупрямые АВ и CD противоположно направлены.

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.

Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулём с чёрточкой (0). О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.

Равенство векторов

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Из данного определения равенства векторов следует, что

равные векторы одинаково направлены и равны по абсолютной величине. Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.

Координаты вектора

Пусть вектор а имеет началом точку А1 (х1; у1), а концом точку А2 (х2; у2). Координатами вектора а будем называть числа а1 = х2 – х1, а2 = у2 – у1. Координаты нулевого вектора равны нулю.

Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны.

Сложение векторов

Суммой векторов а и b с координатами а1, а2 и b1, b2 называется вектор с с координатами a1 +b1, a2 + b2.

Теорема 10.1. Каковы бы ни были точки А, В, С, имеет место векторное равенство АВ + ВС = АС.

Сложение сил

Силу, приложенную к телу, удобно изображать вектором, направление которого совпадает с направлением действия силы, а абсолютная величина пропорциональна величине силы. Как показывает опыт, при таком способе изображения сил равнодействующая двух или нескольких сил, приложенных к телу в одной точке, изображается суммой соответствующих им векторов.

Представление силы в виде суммы сил, действующих в двух заданных направлениях, называется разложением силы по этим направлениям. Удобно производить разложение вектора по двум перпендикулярным осям. В этом случае составляющие вектора называются проекциями вектора на оси.

Умножение вектора на число

Произведением вектора (а1; а2) на число λ называется вектор (λа1; λа2).

Теорема 10.2. Абсолютная величина вектора λа равна |λ| |a|. Направление вектора λа при а ≠ 0 совпадает с направлением вектора а, если λ > 0, и противоположно направлению вектора а, если λ 2 и называется скалярным квадратом.

Для любых векторов а(а1; а2), b(b1; b2), с(с1; с2)
(а + b) • с = ас + bс.

Теорема 10.3. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.

Из теоремы 10.3 следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нулевого векторов равно нулю, то векторы перпендикулярны.

Разложение вектора по координатным осям

Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.

Для любого вектора a (a1; а2) получается разложение а = а1е1 + а2е2.

Вы смотрели «Геометрия 8 Погорелов: все теоремы и определения» — краткое повторение геометрии за 8 класс (основные понятия, определения и теоремы без доказательств ).

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Изучение темы Треугольники в курсе геометрии 7-9 классов средней школы

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

Кафедра математического анализа и

методики преподавания математики

Изучение темы «Треугольники»

в курсе геометрии 7-9 классов средней школы

Выполнила студентка математического

факультета группы М-41

Научный руководитель Ошуева Е.С.

Видео:8 класс, 20 урок, Определение подобных треугольниковСкачать

Введение

Треугольник является важнейшей фигурой планиметрии, и потому в первую очередь изучают свойства этой фигуры. С ним связаны многие методы, используемые при решении различных геометрических задач. Любой многоугольник может быть разделён на треугольники, а изучение свойств этого многоугольника, сводится к изучению составляющих его треугольников. В каком-то смысле изучаемая в школьном курсе геометрия — это геометрия треугольника. Поэтому очень важно представлять себе методику изложения этой темы в различных учебных пособиях для правильного построения курса и избежания методических ошибок.

Данная работа проведена с целью, проследить методику изложения темы «Треугольники» в курсе геометрии 7-9 класса средней школы, а также подготовить конспекты итоговых уроков по данной теме.

Анализ проводится по 4 основным учебникам, наиболее часто встречаемым в школьной практике. Это учебники А.В. Погорелова Геометрия 7-11 (8 издание), Л.С. Атанасяна, Б.Ф. Бутузова и др. Геометрия 7-9, А.П. Киселёва Геометрия 7-9, И.Ф. Шарыгина Геометрия 7-9.

Проанализировать подходы и особенности изложения данной темы.

Проследить соответствие материала учебников содержанию обучения, принятого министерством образования Р.Ф.

Выявить достоинства и недостатки изложения этой темы.

Разработать 4 конспекта уроков итогового повторения.

Видео:Первый признак равенства треугольников. 7 класс.Скачать

§ 1 Анализ школьных учебников по теме: «Треугольники» в 7-9 классе

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

п. 1 Содержание и порядок изложения материала

Л.С. Атанасян и др.

Соотношения между сторонами и углами

Основные свойства простейших геометрических фигур

Смежные и вертикальные

Признаки равенства треугольников

Сумма углов треугольника

Декартовы координаты на плоскости

Понятие об измерении величин

Подобие фигур произвольного вида

Некоторые теоремы о пропорциональных отрезков

Метрические соотношения между элементами треугольника

Пропорциональные линии в круге

тригонометрические функции острого угла

Первые понятия геометрии

Основные свойства плоскости

Треугольник и окружность. Начальные сведения

Виды геометри-ческих задач и методы их решения

Параллельные прямые и углы

Метрические соотношения в треугольнике и окружности

Задачи и теоремы геометрии

Содержание рассмотренных выше учебников соответствует содержанию образования и даже по некоторым вопросам превосходит её.

Видео:Признаки равенства треугольников. 7 класс.Скачать

п. 2 Сравнительный анализ учебников по данной теме

Видео:§ 11 № 1- 69 - Геометрия 7-9 класс ПогореловСкачать

п. п. 1 Определение треугольника

Существуют два подхода к определению треугольника:

1 подход. Понятие треугольника вводится конструктивно: как фигура, состоящая из трёх точек и трёх отрезков соединяющих эти точки. Такой подход реализован в учебнике Атанасяна и в учебнике Погорелова. При этом ничего не говорится о плоскости треугольника. Это делается с целью отступления от теоретико-множественной концепции и от определения равных геометрических фигур с помощью отображений, сохраняющих расстояния (перемещений и движений). Но и здесь есть существенные различия.

В книге Погорелова даётся следующее определение треугольника: «Треугольником называется фигура, которая состоит из трёх точек не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки». Смысл выражения «отрезок соединяет точки» нигде не объяснён. Хотя об этом и легко догадаться; но смысл слова «попарно» совсем не очевиден для семиклассника. Кроме того, определение существенно зависит от обозначений, чего явно в формулировке не указано. В целом, формулировка воспринимается как тяжеловесная и трудная для понимания. У Атанасяна определение чисто конструктивное, оно наглядно и легче воспринимается школьниками.

2 подход. Понятие треугольника даётся как частный случай многоугольника, но в этом понятии говорится не только о фигуре образованной замкнутой линией, но и о части плоскости ограниченной этой замкнутой линией. Этот подход реализован в учебниках Киселёва и Шарыгина. Здесь определение треугольника отдельно не рассматривается. Впоследствии Атанасян и Погорелов всё же обращаются ко второму подходу в теме «Многоугольники» т.к это понятие им потребуется для определения понятия площади.

Определение равенства треугольников во всех четырёх учебниках даётся через совмещение равных фигур путём наложения. Но в учебниках со вторым подходом подразумевается, что и плоскости треугольников также совмещаются наложением.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

п. п. 2 Равнобедренный треугольник

Определение равнобедренного и равностороннего треугольника одинаковое во всех учебниках. Такое определение является общепринятым в математике.

В учебниках Киселёва и Шарыгина свойства равнобедренного треугольника рассматриваются в одной теореме. Доказательства проводятся аналогично, с использованием осевой симметрии относительно биссектрисы треугольника и определения равных треугольников. В силу того, что ни Атанасян, ни Погорелов не используют движения плоскости в 7 классе, основой для доказательства свойств равнобедренных треугольников являются признаки равенства треугольников.

Атанасян в доказательстве свойств равнобедренного треугольника пользуется первым признаком равенства треугольников. В книге Погорелова свойства равнобедренного треугольника доказываются с использованием определения треугольника как упорядоченной тройки точек, но ни где не поясняется, что ΔCAB и ΔCBA это разные треугольники, а не один и тот же по-разному обозначенный. Такое доказательство учениками 7 класса понимается довольно трудно. Автор, уклонившись от явной формулировки определения треугольника как ориентированного пути, ставит ученика лицом к лицу с рассуждениями, которые может понять только тот, кто совершенно чётко представляет себе треугольник как ориентированный путь (это хоть и не явное, но обращение к теоретико-множественному подходу, который так тщательно избегается). Поэтому такие доказательства воспринимаются учениками как цирковой фокус.

Признаки равнобедренного треугольника в учебнике Атанасяна не рассматриваются, хотя эти теоремы очень полезные. В учебнике Погорелова приводится один признак (через равенство углов при основании). Полностью все признаки рассмотрены только у Шарыгина.

Видео:§ 13 № 1- 55 - Геометрия 7-9 класс ПогореловСкачать

п. п. 3 Признаки равенства треугольников

Во всех четырёх учебниках применяется один и тот же подход с использованием аксиомы существования треугольника равного данному. Но нигде ссылок на эту аксиому нет. Доказательства проводятся на основе наглядности с помощью наложения и приложения. В учебнике Погорелова эта аксиома формулируется, но непосредственно при доказательстве на неё ссылки не делаются. Лишь после доказательства первого признака равенства треугольников проводится подробный разбор его с указанием используемых в доказательстве аксиом. Это введено с целью, сделать доказательство более строгим, чем, например доказательство, приведённое у Киселёва. Как нам кажется, именно для этого автор вводит такое нетрадиционное определение треугольника.

Доказательства, приведённые в учебниках Атанасяна и Киселёва аналогичны. Но в учебнике Киселёва, исходя из введенного им определения треугольника, следовало бы ещё доказать, что плоскости треугольников так же совпадут при наложении (о чём в доказательствах даже не упомянуто). В учебнике Атанасяна аксиомы не являются основой, на которой строится школьный курс геометрии (вместе с тем, в приложении в конце учебника подробно изложен вопрос о системе аксиом в курсе геометрии). По нашему мнению, большое преимущество по сравнению с учебным пособием Киселёва, имеет использование в учебнике Атанасяна в качестве основного рабочего аппарата признаки равенства треугольников, а не свойства геометрических преобразований. Такой подход позволяет отработать общие приёмы доказательства теорем. Эти доказательства строятся по схеме: поиск равных треугольников → доказательство предполагаемого равенства → обоснование новых утверждений. Благодаря использованию признаков равенства треугольников легче усваиваются основные теоремы планиметрии (свойства и признаки серединного перпендикуляра, свойства равнобедренного треугольника, теорема о внешнем угле треугольника, свойства и признаки параллельных прямых и параллелограмма, теорема Фалеса, признаки подобия треугольников и т.п.). В учебнике Атанасяна первый признак рассматривается в отрыве от двух других. Это обосновано тем, что он является основой для доказательства свойств равнобедренного треугольника, облегчающих доказательство третьего признака равенства треугольников.

Лишь в учебниках Киселёва и Шарыгина все три признака изучаются последовательно т.к. там не требуется разбивать их для доказательства свойств равнобедренных треугольников.

В учебнике Шарыгина кроме наложения используются ещё и симметрия, что усложняет доказательства. Доказательство третьего признака проводится с использованием элементов построения. Кроме того, применяется движение называемое переносом, но нигде не указано как оно осуществляется и действительно ли переводит одну точку в другую. Кроме трёх традиционных признаков равенства треугольников приводится ещё один для тупого угла и двух не образующих его сторон. Доказательство вытекает из задачи о не существовании треугольника равного данному, если равны две стороны и не содержащийся между ними угол.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

п. п. 4 Признаки подобия треугольников

Определение подобных треугольников даётся как треугольники, у которых соответственные углы равны, а соответственные стороны пропорциональны. Атанасян вводит понятие пропорциональных сходственных сторон. Аналогичное определение приведено в учебнике Киселёва. В учебнике Шарыгина понятие аналогично определению, приведённому у Погорелова, но оно ни как не связано с обозначениями.

Доказательство признаков подобия треугольников в учебнике геометрии А.В. Погорелова основывается на свойствах гомотетии, вывод которых использует формулу расстояния между точками на координатной плоскости и тем самым теорему Пифагора. А теорема Пифагора, в свою очередь, доказывается на основе тригонометрических функций угла, корректность определений которых проверяется с помощью обобщённой теоремы Фалеса, утверждающей, что параллельные прямые, пересекающие стороны угла, отсекают от них пропорциональные отрезки. Ясно, что теорема Фалеса является частью признаков подобия, здесь наблюдается нежелательный в методическом отношении отход от поступательного развития курса. Кроме того, при доказательстве теоремы Фалеса процесс измерения отрезков, и в случае, когда отрезки не соизмеримы, осознавание процесса их измерения происходит у учащихся со значительными трудностями. Этот материал занимает время всего курса геометрии в 8 классе. Теорема Фалеса рассматривается в самом начале 8 класса, а признаки подобия в самом конце 8 класса. В этом плане предпочтительнее расположение материала в учебном пособии Киселёва. Но и у него доказательство признаков подобия основано на такой лемме: прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному. При доказательстве этой леммы рассматриваются отдельно случаи, когда отношение сторон треугольников является либо рациональным, либо иррациональным числом, доказательство усложняется также использованием общей меры и аксиом. А у Атанасяна площади фигур, в отличие от трёх других учебников, рассматриваются раньше, и поэтому удаётся обойти указанную трудность. Фактически она преодолевается один раз при доказательстве свойств пропорциональных отрезков в прямоугольном треугольнике. В этом и состоит одно из преимуществ раннего введения понятия площади.

Как уже видно метод доказательства признаков подобия треугольников в учебнике Атанасяна является существенно другим. Так доказательство первого признака подобия треугольников в этом учебнике основывается на теореме об отношении площадей треугольников, утверждающей, что если в треугольниках ABC и A₁ B₁ C₁ углы А и А₁ равны, то . Эта теорема не является традиционной для школьного курса и скорее всего носит вспомогательный характер. С другой стороны на основе этой теоремы весьма просто доказывается, что отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. По сути дела всё доказательство в одну строчку. Эта же теорема позволяет дать простое доказательство признаков подобия треугольников. В то же время её удалённость от места применения накладывает определённые трудности на усвоение учащимися доказательства признаков подобия треугольников. Здесь лучше модифицировать её, с тем, чтобы её можно было применить непосредственно в теме «Признаки подобия треугольников». У Погорелова такой теоремы нет, что делает невозможным решение его методами задач такого плана:

Треугольники АВС и А₁ В₁ С₁ подобны, их соответствующие стороны относятся как 6: 5. Площадь Δ АВС больше площади Δ А₁ В₁ С₁ на 77 см 2 . Найдите площади треугольников.

В учебнике Шарыгина доказывается терема о пропорциональных отрезках и свойства параллельных прямых. Все три признака подобия формулируются друг за другом, и для всех приводится одно доказательство с некоторыми пояснениями для каждого из признаков. Применяются дополнительные построения для каждого, а дальше используется предыдущая теорема с некоторыми вариациями и признаки равенства треугольников.

Об отношении площадей подобных фигур так же ничего не говорится.

Видео:§ 3 № 1-40 - Геометрия 7-9 класс ПогореловСкачать

§ 2 Конспекты итоговых уроков по теме «Треугольники» для 7-9 классов

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

п. 1 Обобщающий урок по теме «Признаки равенства треугольников»

(По учебнику Погорелова А.В. Геометрия 7-11)

повторить и систематизировать знания учащихся по данной теме;

применить полученные знания для решения задач связанных с треугольниками;

🔍 Видео

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Геометрия 7 класс. Третий признак равенства треугольников (По Погорелову)Скачать

Второй признак равенства треугольников. 7 класс.Скачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Высота, биссектриса, медиана. 7 класс.Скачать