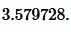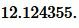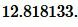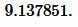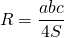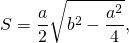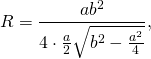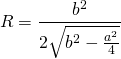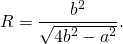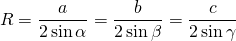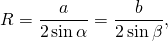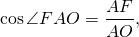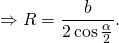С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и боковая сторона b=c
- 2. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и противолежащий угол A
- 3. Радиус окружности описанной около равнобедренного треугольника, если известны боковая сторона b=c треугольника и угол между боковыми сторонами A
- 4. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и прилежащий угол B=C
- Радиус описанной окружности равнобедренного треугольника
- Нахождение радиуса описанной вокруг треугольника окружности
- Формулы вычисления радиуса описанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равносторонний треугольник
- Примеры задач
- 🎥 Видео
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

1. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и боковая сторона b=c
Пусть известны основание a равнобедренного треугольника и боковая сторона b=c. Найдем радиус описанной окружности около равнобедренного треугольника. На странице Радиус окружности описанной около треугольника онлайн была выведена формула вычисления радиуса R описанной около любого треугольника окружности:
| ( small R=frac<large 4 cdot sqrt >. ) | (1) |
где p вычисляется из формулы:
| ( small p= frac. ) | (2) |
Учитывая, что у нас треугольник равнобедренный, т.е. b=c, имеем:
| ( small p= frac=b+ frac, ) | (3) |
| ( small p-a= b- frac, ) | (4) |
| ( small p-b= frac, ) | (5) |
Подставляя (3)−(5) в (1) и учитывая, что b=c, получим:
| ( small R=frac<large 4 cdot frac cdot sqrt<left ( b+fracright)left ( b-fracright)>> ) ( small =frac<large 2 cdot sqrt< b^2-frac>> ) ( small =frac< sqrt> ,) |
| ( small R=frac< sqrt>. ) | (6) |
Пример 1. Известны основание ( small a=7 ) и боковая сторона ( small b=frac ) равнобедренного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (6).
Подставим значения ( small a=7 ) и ( small b=frac ) в (6):
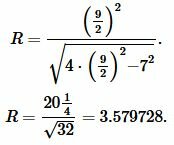 |
Ответ:
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

2. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и противолежащий угол A
Пусть известны сторона a и противолежащий угол A. Формула для нахождения радиуса окружности описанной около равнобедренного треугольника по основанию и противолежащему углу аналогична формуле для нахождения радиуса окружности описанной около произвольного треугольника:
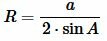 . . | (7) |
Пример 2. Сторона основание равнобедренного треугольника равна:( small a=21 ) а противолежащий угол ( small angle A=60°.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения ( small a=21 ) и ( small angle A=60° ) в (7):
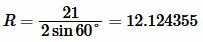 . . |
Ответ:
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

3. Радиус окружности описанной около равнобедренного треугольника, если известны боковая сторона b=c треугольника и угол между боковыми сторонами A
Пусть известны боковая сторона b=c равнобедренного треугольника и угол между боковыми сторонами A. Найдем радиус описанной окружности около равнобедренного треугольника.
На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известных сторонах и углу между ними:
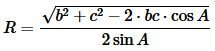 . . | (8) |
Подставляя в (8) c=b, получим:
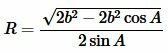 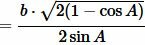 |
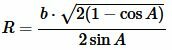 . . | (9) |
Пример 3. Известны основание ( small a=21 ) равнобедренного треугольника и угол между боковыми сторонами: ( small angle A=70°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (9). Подставим значения ( small a=21; ) и ( small angle A=70° ) в (9):
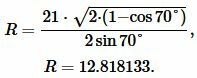 |
Ответ:
Видео:Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать

4. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и прилежащий угол B=C
Пусть известны основание a равнобедренного треугольника и прилежащие к ней угол B=C. Найдем радиус описанной окружности около треугольника. На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известной стороне и прилежащим двум углам:
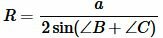 . . | (10) |
Подставляя ( small C=B ) в (10), получим требуемую формулу:
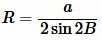 . . | (11) |
Пример 4. Известны основание равнобедренного треугольника ( small a=14 ) и прилежащий к ней угол: ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (11). Подставим значения ( small a=14 ) и ( small angle B=25° ) в (11):
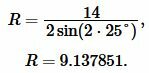 |
Ответ:
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Радиус описанной окружности равнобедренного треугольника
Радиус описанной окружности равнобедренного треугольника можно найти по одной из общих формул радиуса окружности, описанной около треугольника.
Используя свойства равнобедренного треугольника, можно также получить дополнительные формулы.
I. Радиус описанной около треугольника окружности можно найти по формуле
Площадь равнобедренного треугольника через длину основание a и боковую сторону b можно найти по формуле
соответственно, формула для нахождения радиуса описанной окружности для равнобедренного треугольника принимает вид:
верна и для равнобедренного треугольника.
Радиус описанной около равнобедренного треугольника окружности:
где a — основание, b — боковая сторона, α — угол при вершине, β — угол при основании.
III. Радиус описанной окружности в равнобедренном треугольнике можно найти непосредственно, без использования общих формул.
Например, в прямоугольном треугольнике AOF AO=R, AF=b/2, ∠FAO=α/2. Отсюда
IV. В равнобедренном тупоугольном треугольнике центр описанной окружности лежит вне треугольника, напротив его вершины.
Радиус находят по тем же формулам, что и для остроугольного треугольника.
V. В равнобедренном прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, радиус равен половине гипотенузы (то есть половине основания треугольника).
Видео:Формулы равностороннего треугольника #shortsСкачать

Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Видео:Радиус описанной окружностиСкачать

Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
🎥 Видео
Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Геометрия Боковые стороны равнобедренного треугольника равны 4, радиус описанной окружности равенСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

Три способа нахождения радиуса описанной окружности вокруг треугольникаСкачать

Формулы для радиуса окружности #shortsСкачать

Найти радиус вписанной и описанной окружностей равностороннего треугольника. Разные способы.Скачать