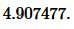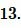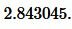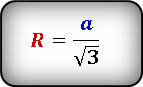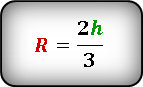С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в равносторонний треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
- 2. Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника
- 3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника
- Радиус описанной окружности равностороннего треугольника
- Нахождение радиуса описанной вокруг треугольника окружности
- Формулы вычисления радиуса описанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равносторонний треугольник
- Примеры задач
- 📸 Видео
Видео:Окружность вписана в равносторонний треугольник, найти радиусСкачать

1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
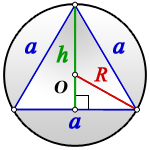
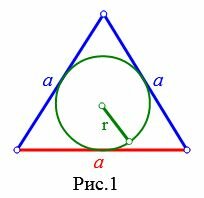
Пусть известна сторона a равностороннего треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
 |
Радиус вписанной в равнобедренный треугольник окружности через основание a и боковую сторону b вычисляется из следующей формулы:
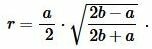 | (1) |
Учитывая, что у равностороннего треугольника все стороны равны (( small a=b )), имеем:
| ( small r=frac cdot sqrt<frac> ) ( small =frac cdot sqrt<frac> ) ( small =frac<large 2 cdot sqrt> ) |
| ( small r=frac<large 2 cdot sqrt> ) | (2) |
или, умножив числитель и знаменатель на ( small sqrt ):
| ( small r=frac<large sqrt> cdot a ) | (3) |
Пример 1. Известна сторона a=17 равностороннего треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (2) и (3). Подставим значения ( small a=17 ) в (3):
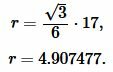 |
Ответ:
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

2. Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника
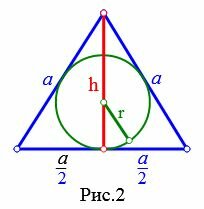
Пусть известна высота h равностороннего треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
 |
Выведем формулу стороны равностороннего треугольника через высоту. Из Теоремы Пифагора имеем:
| ( small h^2+left( frac right) ^2=a^2.) |
| ( small h^2+ frac =a^2; ; ) ( small fraca^2 =h^2; ; ) ( small a^2=frac.) |
| ( small a= frac<large sqrt> .) | (4) |
Формула радиуса вписанной в равнобедренный треугольник окружности по основанию и высоте вычисляется из формулы
| ( small r= large frac<a+sqrt> ) | (5) |
Подставляя (4) в (5), получим:
| ( small r= large frac<frac<large sqrt>><frac<large sqrt>+sqrt<frac+4h^2>> ) ( small = large frac<frac<large sqrt>><frac<large sqrt>+sqrt<frac>> ) ( small = large frac<frac<large sqrt>><frac<large sqrt>+frac<large sqrt>> ) ( small = large fracsmall =large frac small cdot h ) |
То есть, радиус вписанной в равносторонний треугольник окружности по высоте вычисляется из формулы:
| ( small r = large frac small cdot h ) | (6) |
Пример 2. Известна высота ( small h=39 ) равностороннего треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значение ( small h=39 ) в (6):
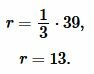 |
Ответ:
Видео:Вписанная окружность в равностороннем треугольникеСкачать

3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника
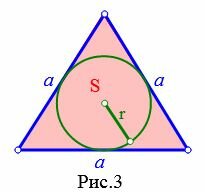
Пусть известна площадь S равностороннего треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
 |
Площадь равностороннего треугольника по радиусу вписанной окружности вычисляется из следующей формулы:
| ( small S= 3cdot sqrtr^2.) |
| ( small r^2= large frac |
| ( small r= large frac <sqrt[4]> small cdot sqrt | (7) |
Пример 3. Известна площадь равностороннего треугольника: ( small S=42 . ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (7). Подставим значение ( small S=42 ) в (7):
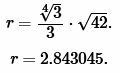 |
Ответ:
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Радиус описанной окружности равностороннего треугольника



Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне
Формула радиуса описанной окружности равностороннего треугольника через высоту:
Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне
Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
📸 Видео
Равносторонний треугольник в окружностиСкачать

Радиус окружности описанной около равностороннего треугольникаСкачать
найти радиус окружности, описанной вокруг треугольникаСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия. Площади. Задача №9. Геометрия в жизни. Задача №10Скачать

Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать

Формулы равностороннего треугольника #shortsСкачать

2065 радиус окружности вписанной в правильный треугольник равен 29 Найдите высоту этого треугольникаСкачать

Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

Найти радиус описаной окружности в равностороннем треугольникеСкачать

Найти радиус вписанной и описанной окружностей равностороннего треугольника. Разные способы.Скачать

ОГЭ ЗАДАНИЕ 16 РАЗДЕЛ ГЕОМЕТРИЯ ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК И ОКРУЖНОСТЬСкачать