| Главная | Шутки | Форум |
|
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности Круг |  Конечная часть плоскости, ограниченная окружностью Радиус |  Отрезок, соединяющий центр окружности с любой точкой окружности Хорда |  Отрезок, соединяющий две любые точки окружности Диаметр |  Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности Касательная |  Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания Секущая |  Прямая, пересекающая окружность в двух точках Видео:8 класс, 32 урок, Касательная к окружностиСкачать  Свойства хорд и дуг окружности
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. Диаметр, проходящий через середину хорды |  Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. Равные хорды |  Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. Хорды, равноудалённые от центра окружности |  Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. Две хорды разной длины |  Большая из двух хорд расположена ближе к центру окружности. Равные дуги |  У равных дуг равны и хорды. Параллельные хорды |  Дуги, заключённые между параллельными хордами, равны. Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать  Теоремы о длинах хорд, касательных и секущих
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Касательные, проведённые к окружности из одной точки |  Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. Касательная и секущая, проведённые к окружности из одной точки |  Секущие, проведённые из одной точки вне круга | 
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Касательные, проведённые к окружности из одной точки | Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. Касательная и секущая, проведённые к окружности из одной точки | Секущие, проведённые из одной точки вне круга | Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать  Доказательства теорем о длинах хорд, касательных и секущихТеорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1). Тогда справедливо равенство Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство откуда и вытекает требуемое утверждение. Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2). Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство откуда и вытекает требуемое утверждение. Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3). Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство Доказательство . Проведём из точки A касательную AB к окружности (рис. 4). Точка B – точка касания. В силу теоремы 2 справедливы равенства откуда и вытекает требуемое утверждение. Видео:Уравнение окружности (1)Скачать  Теорема о бабочкеТеорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны. Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения: Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим Воспользовавшись теоремой 1, получим Воспользовавшись равенствами (1) и (2), получим Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство откуда вытекает равенство что и завершает доказательство теоремы о бабочке. Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать  Касательная к окружностиО чем эта статья: Видео:Радиус и диаметрСкачать  Касательная к окружности, секущая и хорда — в чем разницаВ самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу. Касательная к окружности — это прямая, имеющая с ней всего одну общую точку. Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ). Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой. Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать  Свойства касательной к окружностиВыделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку. Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны. Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ. Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС. В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания. Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ. Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом. ЗадачаУ нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ. Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°. Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла. ∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62° Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°. Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны. Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD. Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°. Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны. Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам. Задача 1У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные. Решение Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA. ∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°). Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами: ∠BDC = ∠BDA × 2 = 30° × 2 = 60° Итак, угол между касательными составляет 60°. Задача 2К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК. Решение Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным. Углы при его основании будут равны, т.е. ∠МNК = ∠NМК. ∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65° Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть. Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения. Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей. Задача 1Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA. Решение Исходя из соотношения касательной и секущей МА 2 = МВ × МС. Найдем длину внешней части секущей: МС = МВ — ВС = 16 — 12 = 4 (см) МА 2 = МВ × МС = 16 х 4 = 64 Задача 2Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO. Решение Допустим, что МО = у, а радиус окружности обозначим как R. В таком случае МВ = у + R, а МС = у – R. Поскольку МВ = 2 МА, значит: МА = МВ : 2 = (у + R) : 2 Согласно теореме о касательной и секущей, МА 2 = МВ × МС. (у + R) 2 : 4 = (у + R) × (у — R) Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим: Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см). Ответ: MO = 10 см. Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними. Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC. Задача 1Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой. Решение Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ. АВ = ∠АВС × 2 = 32° × 2 = 64° Задача 2У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK. Решение Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно: КМ = 2 ∠МКВ = 2 х 84° = 168° Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный. ∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2 Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то: ∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6° Видео:Радиус описанной окружностиСкачать  Геометрия. Урок 5. ОкружностьСмотрите бесплатные видео-уроки на канале Ёжику Понятно. Видео-уроки на канале Ёжику Понятно. Подпишись! Содержание страницы:
Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать  Определение окружностиОкружность – геометрическое место точек, равноудаленных от данной точки. Эта точка называется центром окружности . Видео:Окружность, диаметр, хорда геометрия 7 классСкачать  Отрезки в окружностиРадиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности. Хорда a – отрезок, соединяющий две точки на окружности. Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ). O A – радиус, D E – хорда, B C – диаметр. Теорема 1: Касательная к окружности – прямая, имеющая с окружностью одну общую точку. Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности. Теорема 2: Теорема 3: Видео:№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать  Дуга в окружностиЧасть окружности, заключенная между двумя точками, называется дугой окружности . Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B . Теорема 4: Если A B = C D , то ∪ A B = ∪ C D Видео:КАК НАЙТИ РАДИУС ОКРУЖНОСТИ? КАСАТЕЛЬНАЯ И РАДИУС #shorts #математика #егэ #огэСкачать  Углы в окружностиВ окружности существует два типа углов: центральные и вписанные. Центральный угол – угол, вершина которого лежит в центре окружности. ∠ A O B – центральный. Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается. Градусная мара всей окружности равна 360 ° . Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность. ∠ A C B – вписанный. Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α Теорема 5: ∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2 Теорема 6: ∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 ° Видео:Составить уравнения касательных к окружности (x-1)2+(y+3)2=40, перпендикулярных прямой 3x+y-4=0Скачать  Длина окружности, длина дугиМы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α . Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α . Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси. Длина окружности находится по формуле: Длина дуги окружности , на которую опирается центральный угол α равна: l α = π R 180 ∘ ⋅ α Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Площадь круга и его частейТеперь поговорим про площадь круга, площадь сектора и площадь сегмента. Круг – часть пространства, которая находится внутри окружности. Иными словами, окружность – это граница, а круг – это то, что внутри. Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо. Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка. Площадь круга находится по формуле: S = π R 2 Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Примеры сектора в реальной жизни: кусок пиццы, веер. Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу. Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы. Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой. S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать  Теорема синусовЕсли вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов: a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности. Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать  Примеры решений заданий из ОГЭМодуль геометрия: задания, связанные с окружностями. Видео:9 класс, 6 урок, Уравнение окружностиСкачать  Радиус — что это такое и как найти радиус окружностиЧерез длину стороныФормула для нахождения длины окружности через радиус: , где r — радиус окружности. Найти радиус круга, зная окружность
Окружность круга P | Результат | Радиус и диаметрРадиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет. А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Обозначается диаметр также первой буквой своего слова – D или d. Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Вычисление радиусаРадиус можно посчитать разными способами. Если известен диаметрЭтот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2. Если известна длина окружности кругаТакже несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус. Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так: Означает данное значение отношение длины окружности к диаметру той же окружности. Если известна площадь кругаФормула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса: В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса. Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок. Способ расчета радиуса круга:Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга). Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга). Через сторону описанного квадратаСторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
Как посчитать радиус зная длину окружностиЧему равен радиус (r) если длина окружности C? Формулаr = C /2π , где π ≈ 3.14 Свойства радиусаВ отношении радиуса действуют несколько важных правил:
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра. По площади сектора и центральному углу
Площадь сегментаРассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла . Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем В случае, когда величина α выражена в в радианах , получаем Формулы для площади круга и его частей
где R – радиус круга, D – диаметр круга Площадь сектора | | 
если величина угла α выражена в радианах
если величина угла α выражена в градусах Площадь сегмента | | 
если величина угла α выражена в радианах
если величина угла α выражена в градусах Центральный угол, вписанный угол и их свойстваСвязанные определения
Примеры задачЗадание 1 Решение: Задание 2 Решение: Длина дугиРассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла . В случае, когда величина α выражена в градусах , справедлива пропорция из которой вытекает равенство: В случае, когда величина α выражена в радианах , справедлива пропорция из которой вытекает равенство: Уравнение окружностиr 2 = ( x – a ) 2 + ( y – b ) 2 3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
Углы между двумя хордамиСлучай 1: два секущие пересекаются внутри окружности. Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности. Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются. Через площадь и полупериметр описанного треугольникаРазделите площадь описанного треугольника на его полупериметр.
Основные свойства касательных к окружности3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной: Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны: ОбобщенияРадиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен Через диагональ вписанного прямоугольникаДиагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
Площадь круга, онлайн расчетКак найти площадь круга по формуле через радиус либо диаметр круга. | Площадь круга, онлайн расчет | Вместо заключенияЧтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так. Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||








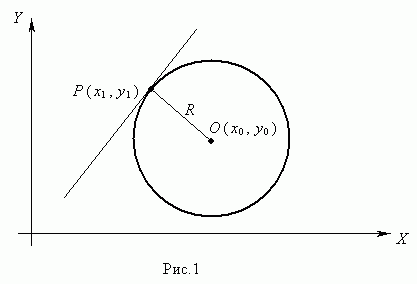


 Отрезки и прямые, связанные с окружностью
Отрезки и прямые, связанные с окружностью














































































 ,
, ,
, ,
, ,
, ,
,










