Как найти площадь трапеции вписанной в окружность

Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.

Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.

Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм 2 , см 2 , м 2 и км 2 и так далее.

Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.

Формулы площади трапеции

Площадь любых трапеций

Ⅰ. Площадь трапеции через основания и высоту:

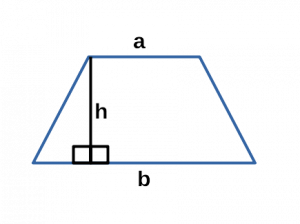
[ S = frac cdot h ]
a,b — основания трапеции;
h — высота трапеции;

Ⅱ. Площадь трапеции через высоту и среднюю линию:

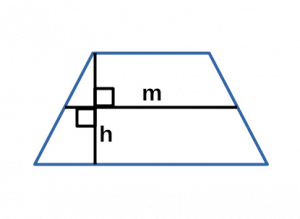
[ S = mh ]
m — средняя линия трапеции;
h — высота трапеции;

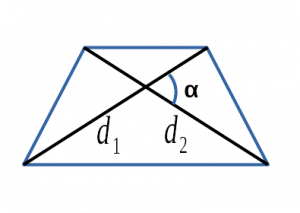
Ⅲ. Площадь трапеции через диагонали и угол между ними:

[ S =fracd_1d_2 cdot sin alpha ]
( d_1, d_2 ) ​​- диагонали трапеции;
sin α — синус угла альфа в трапеции;

Ⅳ. Площадь трапеции через периметр, высоту и боковые стороны:

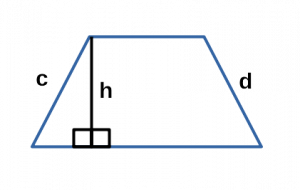
[ S = frach ]
P — периметр трапеции;
c,d — боковые стороны трапеции;
h — высота трапеции;

Ⅴ. Площадь трапеции через основания и боковые стороны:
[ S = frac cdot sqrt<c^2-(frac)^2> ]
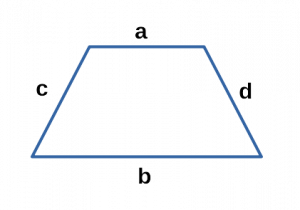
a,b — основания трапеции;
с,d — боковые стороны трапеции;

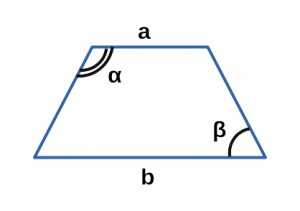
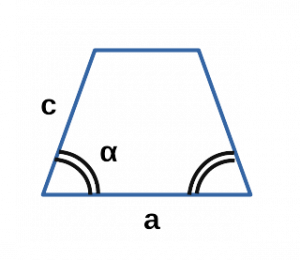
Ⅵ. Площадь трапеции через основания и углы:

a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;

Площадь равнобедренной трапеции

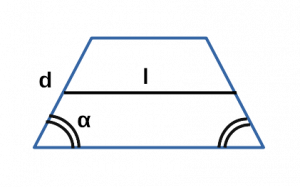
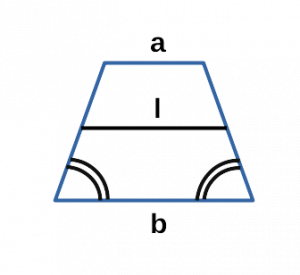
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:

[ S = ld cdot sin α ]

l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

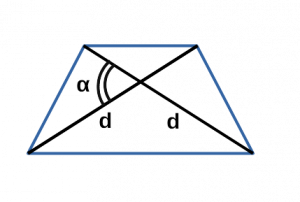
Ⅱ. Площадь трапеции через диагонали и синус угла:

[ S = frac cdot sin α ]

d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

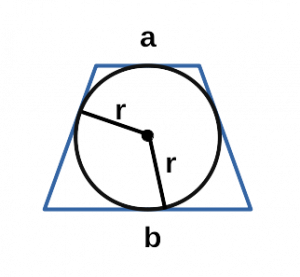
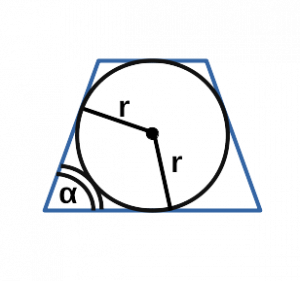
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:

r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;

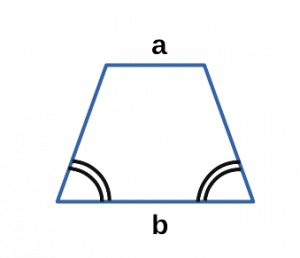
Ⅳ. Площадь трапеции через основания:

a, b — основания равнобедренной трапеции;

Ⅴ. Площадь трапеции через основания и среднюю линию:

l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;

Ⅵ. Площадь трапеции через синус угла и стороны:

[ S = c cdot sin α cdot (a-c cdot cos α) ]

a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;

Ⅶ. Площадь трапеции через угол и радиус вписанной окружности:

r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

Определения трапеции

Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.

Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:

• Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
• Равнобедренная / равнобочная / равнобоковая трапеция:
  два угла при основании равны, две боковые стороны равны.
• Прямоугольная / прямаятрапеция: один из углов прямой.

Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.

Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.

Элементы трапеции

Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.

Основание трапеции — это сторона, противолежащая
сторона которой параллельна.

Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.

Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.

Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.

Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.

Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.

Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.

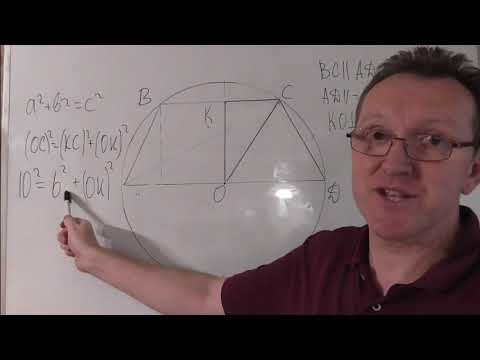
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:Трапеция, вписанная в окружностьСкачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Окружность, вписанная в трапециюСкачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:Трапеция и вписанная окружностьСкачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Радиус описанной окружности трапецииСкачать

Площадь трапеции

Видео:Трапеция вписана в окружность. Найти радиус окружностиСкачать

Что такое трапеция

Трапеция — это плоская фигура, ее изучают в курсе геометрии 8 класса.

Трапеция — четырехугольник, две стороны которого параллельны, и две другие стороны не параллельны.

Основаниями называются параллельные стороны трапеции. Непараллельные — боковые стороны.

Частный случай трапеции — равнобедренная трапеция, боковые стороны которой равны. Трапеция с углами по 90 градусов, прилежащими к одной боковой стороне, называется прямоугольной.

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон и параллельный основаниям.

ABCD — трапеция, EF — ее средняя линия, BC||EF||AD, BE=CF, AE=DF.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Формулы площади трапеции

Чтобы найти площадь трапеции можно использовать несколько формул. Выбор зависит от данных условия.

Площадь трапеции равна произведению половины суммы ее оснований на высоту.

Рассмотрим трапецию ABCD, AD||BC, BF — высота. S A B C D = A A + B C 2 B F . Если A D = a , B C = b , B F = h , формула для нахождения площади трапеции будет выглядеть как S = a + b 2 · h .

Площадь трапеции равна произведению ее средней линии на высоту.

Для данной трапеции S A B C D = M N · B F , а формула выглядит так: S=h·m, где h — высота, m — средняя линия.

Площадь трапеции равна половине произведения ее диагоналей на синус угла между ними.

S A B C D = ½ A C · B D · s i n ∠ C O D или S A B C D = ½ A C · B D · s i n ∠ B O C , так как sin ∠ C O D = sin ∠ B O C . Формула для нахождения площади трапеции через диагонали: S = ½ d 1 · d 2 · s i n φ .

У трапеции, диагонали которой перпендикулярны, S = ½ d 1 · d 2 , так как sin 90º=1.

Площадь трапеции равна произведению половины ее периметра на радиус вписанной окружности. Если суммы противолежащих сторон трапеции равны, то в трапецию можно вписать окружность. Полупериметр трапеции равен половине суммы ее четырех сторон или сумме ее оснований. Зная основания трапеции и радиус вписанной окружности, можно посчитать ее площадь: S = a + b r , где a и b — основания, r — радиус вписанной окружности. Радиус вписанной в трапецию окружности равен половине высоты трапеции h, поэтому из формулы S = a + b r можно получить S = a + b 2 · h .

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Формула площади равнобедренной трапеции

Площадь равнобедренной трапеции можно рассчитать по тем же формулам. Некоторые из них имеют упрощенный вид.

1. Если известны основания a и b и высота трапеции h, то площадь рассчитывают как и в общем случае: S = a + b 2 · h .
2. S=h·m, где h — высота, m — средняя линия.
3. Площадь равнобедренной трапеции равна половине произведения её диагоналей d 1 и d 2 на синус угла между ними. У равнобедренной трапеции d 1 = d 2 ⇒ S = ½ d 2 · s i n φ (половине произведения квадрата ее диагонали на синус угла между диагоналями).

Площадь равнобедренной трапеции с перпендикулярными диагоналями

• Так как sin 90º=1, то S = ½ d 2 · s i n φ = ½ d 2 .
• Площадь равнобедренной трапеции, диагонали которой перпендикулярны, равна квадрату ее высоты: S = h 2 .
• Если в трапецию можно вписать окружность, то применяется общая формула S = a + b r .

Видео:Найти высоту в трапеции вписанной в окружностьСкачать

Формула площади криволинейной трапеции

Криволинейная трапеция — это плоская фигура, ограниченная графиком непрерывной и неотрицательной на отрезке [а;b] функции y=f(х), прямыми х=а, x=b и осью абсцисс.

Отрезок [a;b] называют основанием криволинейной трапеции. Отрезки, ограничивающие криволинейную трапецию слева и справа, могут вырождаться в точку. Верхняя граница криволинейной трапеции может быть задана разными формулами на разных частях отрезка.

Формула Ньютона-Лейбница

Нахождение площади криволинейной трапеции рассматривают в 11 классе как пример применения интеграла.

Площадь криволинейной трапеции, образованной графиком функции y=f(x) на интервале [a;b] записывают в виде определенного интеграла: S = ∫ a b f ( x ) d x .

По формуле Ньютона-Лейбница определенный интеграл равен: ∫ a b f ( x ) d x = F ( x ) | a b = F ( a ) − F ( b ) .

Видео:Задача про трапецию, описанную около окружностиСкачать

Пояснение на примерах

Найдите площадь трапеции, если ее основания равны 4 и 7 см, а высота — 4 см.

Чтобы узнать площадь трапеции, используем формулу S = a + b 2 · h : S = 1 / 2 · ( 4 + 7 ) · 4 = 22 ( с м 2 ) .

Найдите площадь фигуры под кривой на заданном интервале: f(x)=x3+3, x∈[−1;1].

📺 Видео

Задание 26_Равнобедренная трапеция. Вписанная окружность.Скачать

Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делитсяСкачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Трапеция вписанная в окружностьСкачать

Трапеция, вписанная в окружностьСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия В прямоугольную трапецию вписана окружность. Найдите её радиус, если основания трапецииСкачать

Трапеция в окружности. Задача Шаталова.Скачать