Как найти периметр треугольника координатами (3 видео)

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Содержание

Как найти периметр треугольника, заданного координатами своих вершин
Как найти периметр треугольника
Определение
Как узнать периметр треугольника
Скачать онлайн таблицу
🌟 Видео

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Как найти периметр треугольника, заданного координатами своих вершин

Периметр — это длина линии, ограничивающей занимаемую плоской геометрической фигурой площадь. Для , как и всех других многоугольников, это ломаная линия, составленная из его всех его сторон. Поэтому задача вычисления периметра треугольника, заданного координатами его вершин, сводится к вычислению длины каждой из сторон с последующим суммированием полученных величин.

Чтобы вычислить длину стороны, рассмотрите вспомогательный треугольник, составленный из самой стороны и двух ее проекций на оси абсцисс и ординат. В этой фигуре две проекции будут образовывать прямой угол — это вытекает из определения прямоугольных координат. Это означает, что они будут катетами в прямоугольном треугольнике, где гипотенузой будет сама сторона. Ее длину можно вычислить по теореме Пифагора, надо лишь найти длины проекций (катетов). Каждая из проекций представляет собой отрезок, начальная точка которого определена меньшей координатой, конечная — большей, а их разница и будет длиной проекции.

Рассчитайте длину каждой стороны. Если обозначить координаты точек, определяющих треугольник, как A(X₁,Y₁), B(X₂,Y₂) и C(X₃,Y₃), то для стороны АВ проекции на оси абсцисс и ординат будут иметь длины X₂-X₁ и Y₂-Y₁, а длина самой стороны в соответствии с теоремой Пифагора будет равна АВ = √((X₂-X₁)² + (Y₂-Y₁)²). Длины двух других сторон, рассчитанные через их проекции на оси координат, можно записать так: ВС = √(( X₃-X₂)² + (Y₃-Y₂)²), СА = √((X₃-X₁)² + (Y₃-Y₁)²).

При использовании трехмерной системы координат в подкоренное выражение, полученное на предыдущем шаге, добавьте еще одно слагаемое, которое должно выражать квадрат длины проекции стороны на ось аппликат. В этом случае координаты точек можно записать так: A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃). А формулы расчета длин сторон примут такой вид: АВ = √((X₂-X₁)² + (Y₂-Y₁)² + (Z₂- Z₁)²), ВС = √(( X₃-X₂)² + (Y₃-Y₂)² + (Z₃-Z₂)²) и СА = √((X₃-X₁)² + (Y₃-Y₁)² + (Z₃-Z₁)²).

Рассчитайте периметр (Р) треугольника, сложив полученные на предыдущих шагах длины сторон. Для плоской Декартовой системы координат формула в общем виде должна выглядеть так: Р = АВ + ВС + СА = √((X₂-X₁)² + (Y₂-Y₁)²) + √(( X₃-X₂)² + (Y₃-Y₂)²) + √((X₃-X₁)² + (Y₃-Y₁)²). Для трехмерных координат эта же формула должна иметь такой вид: Р = √((X₂-X₁)² + (Y₂-Y₁)² + (Z₂- Z₁)²) + √(( X₃-X₂)² + (Y₃-Y₂)² + (Z₃-Z₂)²) + √((X₃-X₁)² + (Y₃-Y₁)² + (Z₃-Z₁)²).

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать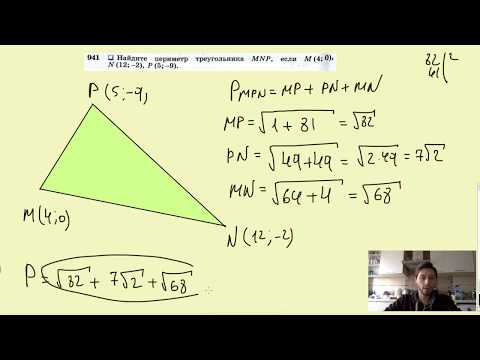

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Видео:КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Видео:Уравнения стороны треугольника и медианыСкачать

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.